3.1. Однородное уравнение
Определение. Линейным уравнением n-го порядка называется уравнение вида:
 . (3.1)
. (3.1)
Если при всех рассматриваемых значениях x функция 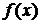 равна нулю, то это уравнение называется однородным, в противном случае – неоднородным.
равна нулю, то это уравнение называется однородным, в противном случае – неоднородным.
Предполагаем, что коэффициенты 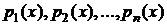 и свободный член
и свободный член 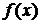 определены и непрерывны в интервале
определены и непрерывны в интервале 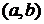 . Тогда уравнение (3.1) имеет единственное решение
. Тогда уравнение (3.1) имеет единственное решение  , определённое во всём интервале
, определённое во всём интервале 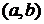 и удовлетворяющее начальным условиям:
и удовлетворяющее начальным условиям:
 ,
,
причём начальные данные  можно задавать произвольно, а
можно задавать произвольно, а  нужно брать из интервала
нужно брать из интервала 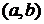 .
.
Заметим, что линейное однородное дифференциальное уравнение (ЛОДУ) всегда имеет нулевое решение  .
.
Для построения общего решения ЛОДУ достаточно знать n линейно независимых в интервале 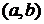 частных решений
частных решений  , т.е. таких решений, для которых тождество
, т.е. таких решений, для которых тождество
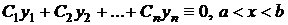 ,
,
(где  – постоянные числа,) может выполняться только при
– постоянные числа,) может выполняться только при  . Такая система решений называется фундаментальной. Известно, что для того чтобы система решений ЛОДУ была фундаментальной, необходимо и достаточно, чтобы её определитель Вронского
. Такая система решений называется фундаментальной. Известно, что для того чтобы система решений ЛОДУ была фундаментальной, необходимо и достаточно, чтобы её определитель Вронского
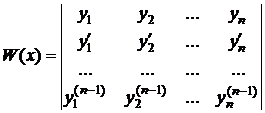
был отличен от нуля хотя бы в одной точке из интервала 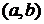 . В действительности, в этом случае определитель Вронского отличен от нуля во всех точках интервала
. В действительности, в этом случае определитель Вронского отличен от нуля во всех точках интервала 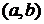 .
.
Если найдена фундаментальная система решений  ЛОДУ, то формула
ЛОДУ, то формула
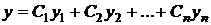 , (3.2)
, (3.2)
где  – произвольные постоянные, даёт общее решение этого уравнения в области
– произвольные постоянные, даёт общее решение этого уравнения в области  ,
, 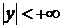 ,
,  , …,
, …,  .
.
3.2. Линейное однородное дифференциальное уравнение
с постоянными коэффициентами
Линейное однородное дифференциальное уравнение с постоянными коэффициентами имеет вид:
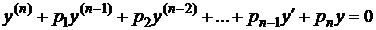 , (3.3)
, (3.3)
где  – постоянные вещественные числа. Это уравнение имеет фундаментальную систему решений
– постоянные вещественные числа. Это уравнение имеет фундаментальную систему решений  , определённую при всех x и состоящую из степенных, показательных и тригонометрических функций. Соответствующее этой системе функций общее решение
, определённую при всех x и состоящую из степенных, показательных и тригонометрических функций. Соответствующее этой системе функций общее решение
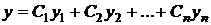
определено в области  ,
, 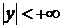 ,
,  , …,
, …,  , т.е. во всём пространстве
, т.е. во всём пространстве  .
.
Построение фундаментальной системы решений ЛОДУ проводится методом Эйлера, который состоит в том, что частное решение ЛОДУ ищется в виде  , где
, где  – некоторое число, подлежащее определению. Подставляя эту функцию в уравнение (3.3) и сокращая на
– некоторое число, подлежащее определению. Подставляя эту функцию в уравнение (3.3) и сокращая на  ,получим характеристическое уравнение:
,получим характеристическое уравнение:
 . (3.4)
. (3.4)
Его корни называются характеристическими числами уравнения (3.3). Рассмотрим возможные ситуации, возникающие при решении характеристического уравнения.
1. Все корни характеристического уравнения (3.4) различны и вещественны. Обозначим их 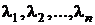 . Тогда фундаментальную систему решений составляют функции:
. Тогда фундаментальную систему решений составляют функции:  , а общее решение имеет вид:
, а общее решение имеет вид:
 .
.
2. Все корни характеристического уравнения (3.4) различны, но среди них имеются комплексные. Пусть  – комплексный корень характеристического уравнения. Тогда
– комплексный корень характеристического уравнения. Тогда  тоже будет корнем этого уравнения. Этой паре корней соответствует пара линейно независимых частных решений:
тоже будет корнем этого уравнения. Этой паре корней соответствует пара линейно независимых частных решений:
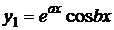 ,
,
 .
.
Записав линейно независимые частные решения, соответствующие другим сопряжённым парам комплексных корней и всем вещественным корням, получим фундаментальную систему решений. Линейная комбинация этих решений с произвольными постоянными коэффициентами даст общее решение уравнения (3.3).
3. Среди корней характеристического уравнения имеются кратные. Пусть  – вещественный k -кратный корень. Тогда ему соответствует k линейно независимых частных решений вида
– вещественный k -кратный корень. Тогда ему соответствует k линейно независимых частных решений вида  , а в формуле общего решения – выражение вида
, а в формуле общего решения – выражение вида  .
.
4. Если  – комплексный корень характеристического уравнения кратности k, то ему и сопряжённому с ним корню
– комплексный корень характеристического уравнения кратности k, то ему и сопряжённому с ним корню  той же кратности соответствуют 2 k линейно независимых частных решений вида:
той же кратности соответствуют 2 k линейно независимых частных решений вида:

В формуле общего решения этим корням соответствует выражение вида:
 .
.
Записав линейно независимые частные решения указанного выше вида, соответствующие всем простым и кратным вещественным корням, а также сопряжённым парам простых и кратных комплексных корней, получим фундаментальную систему решений. Линейная комбинация этих решений с произвольными постоянными коэффициентами даст общее решение уравнения (3.3).
4. Системы обыкновенных
дифференциальных уравнений
4.1. Нормальные системы
Определение 1. Нормальная система обыкновенных дифференциальных уравнений имеет следующий вид:
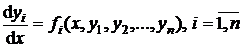 , (4.1)
, (4.1)
где  ,
,  – неизвестные функции от независимой переменной x, подлежащие определению;
– неизвестные функции от независимой переменной x, подлежащие определению; 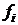 ,
,  – известные функции от
– известные функции от  , заданные и непрерывные в некоторой области. Число n называется порядком системы (4.1). В дальнейшем ограничимся рассмотрением систем второго порядка (
, заданные и непрерывные в некоторой области. Число n называется порядком системы (4.1). В дальнейшем ограничимся рассмотрением систем второго порядка (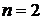 ).
).
Определение 2. Пусть дана нормальная система уравнений
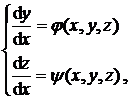 (4.2)
(4.2)
где  и
и  – заданные непрерывные в некоторой области функции. Пара функций
– заданные непрерывные в некоторой области функции. Пара функций  , определённых на интервале
, определённых на интервале 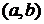 , имеющих непрерывные производные и удовлетворяющих на
, имеющих непрерывные производные и удовлетворяющих на 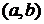 обоим уравнениям системы (4.2), называется её решением.
обоим уравнениям системы (4.2), называется её решением.
Задача нахождения решения  , удовлетворяющего начальным условиям
, удовлетворяющего начальным условиям  , где
, где  – заданные числа (начальные данные), называется задачей Коши.
– заданные числа (начальные данные), называется задачей Коши.
Теорема существования и единственности решения задачи Коши. Пусть дана система уравнений (4.2) и пусть в некоторой области D (x, y, z) функции 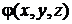 и
и  непрерывны и имеют непрерывные частные производные по y, z. Пусть точка
непрерывны и имеют непрерывные частные производные по y, z. Пусть точка  . Тогда существуют интервал
. Тогда существуют интервал 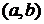 и определённые на нем непрерывно дифференцируемые функции
и определённые на нем непрерывно дифференцируемые функции  , удовлетворяющие системе уравнений (4.2) и начальным условиям
, удовлетворяющие системе уравнений (4.2) и начальным условиям  , причём эти функции определяются однозначно.
, причём эти функции определяются однозначно.
4.2. Метод исключения
Продифференцируем, например, первое уравнение системы уравнений (4.2) по независимой переменной x:

 .
.
Вместо системы (4.2) запишем систему уравнений:
 (4.3)
(4.3)
Из первого уравнения системы (4.3) следует, что  . Подставим эту функцию во второе уравнение системы (4.3):
. Подставим эту функцию во второе уравнение системы (4.3):
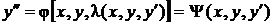 .
.
Итак, исключив из системы функцию z приходим к одному уравнению 2-го порядка, решая которое, получаем: 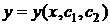 .
.
Теперь продифференцируем найденное выражение по x и подставим в функцию  , получим
, получим 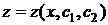 .
.
В результате заключаем, что решение примет вид:
 (4.4)
(4.4)
Определение. Общим решением системы двух обыкновенных дифференциальных уравнений 1-го порядка является совокупность функций (4.4), непрерывно дифференцируемых на некотором интервале 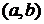 , которые при различных допустимых значениях произвольных постоянных удовлетворяют обоим уравнениям системы уравнений (4.2). При этом в области, в которой выполнены условия теоремы существования и единственности, можно получить решение любой задачи Коши.
, которые при различных допустимых значениях произвольных постоянных удовлетворяют обоим уравнениям системы уравнений (4.2). При этом в области, в которой выполнены условия теоремы существования и единственности, можно получить решение любой задачи Коши.
4.3. Линейные однородные системы
дифференциальных уравнений (ЛОС ДУ)
Определение. Линейной однородной системой дифференциальных уравнений (ЛОС ДУ) для функций  называется система уравнений вида
называется система уравнений вида
 (4.5)
(4.5)
где  – непрерывные на некотором интервале
– непрерывные на некотором интервале 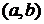 функции.
функции.
Свойства решений ЛОС ДУ (4.5).
1. Сумма двух решений системы (4.5) – тоже решение этой системы.
Доказательство: Пусть  и
и  – два каких-либо решения системы (4.5).
– два каких-либо решения системы (4.5).
Тогда


Но  и
и  .
.
Аналогично рассматривается и второе уравнение системы (4.5).
2. Если  – решение ЛОС ДУ и c – произвольная константа, то
– решение ЛОС ДУ и c – произвольная константа, то  – тоже решение (4.5).
– тоже решение (4.5).
Доказательство свойства аналогично доказательству свойства 1.
Следствие. Если  и
и  – решения системы (4.5), то выражение вида
– решения системы (4.5), то выражение вида

где 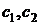 – произвольные постоянные, тоже решение (4.5).
– произвольные постоянные, тоже решение (4.5).
Определение 1. Система функций  и
и 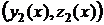 называется линейно независимой на некотором интервале
называется линейно независимой на некотором интервале 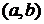 , если из системы равенств
, если из системы равенств
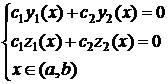 (4.6)
(4.6)
следует, что  .
.
В противном случае система функций  и
и 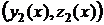 называется линейно зависимой на интервале
называется линейно зависимой на интервале 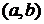 .
.
Определение 2. Определитель, составленный для системы функций  и
и 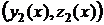 , называется определителем Вронского и обозначается W (x), т.е.
, называется определителем Вронского и обозначается W (x), т.е.
 .
.
Теорема 1. Определитель Вронского для линейно независимой на интервале 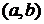 системы решений
системы решений  и
и 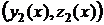 ЛОС ДУ не равен нулю ни в одной точке интервала
ЛОС ДУ не равен нулю ни в одной точке интервала 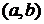 .
.
Доказательство. Докажем теорему методом от противного. Предположим, что существует точка  , в которой
, в которой
 .
.
Составим линейную однородную систему уравнений с неизвестными  и
и  :
:
 . (4.7)
. (4.7)
Так как определитель системы (4.7) равен нулю, то система имеет бесконечное множество ненулевых решений. Пусть  – одно из них. С помощью этих констант и двух линейно независимых на интервале
– одно из них. С помощью этих констант и двух линейно независимых на интервале 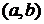 решений системы (3.1)
решений системы (3.1)  и
и 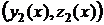 составим две функции
составим две функции
 (4.8)
(4.8)
Согласно следствию из свойств решений ЛОС ДУ функции (4.8) являются решениями системы (4.5), которые в силу равенств (4.7) в точке  обращаются в нуль. Следовательно,
обращаются в нуль. Следовательно,  – решение следующей задачи Коши:
– решение следующей задачи Коши:

Но таким решением может быть только нулевое решение:  при любом
при любом  , т.е.
, т.е.

Причём  . Это означает, что система функций
. Это означает, что система функций  и
и 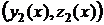 линейно зависима на интервале
линейно зависима на интервале  , что противоречит условию теоремы. Значит наше предположение о существовании на интервале
, что противоречит условию теоремы. Значит наше предположение о существовании на интервале  точки
точки  , в которой
, в которой 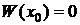 , неверно, что и доказывает теорему.
, неверно, что и доказывает теорему.
Определение 2. Линейно независимые на интервале  решения ЛОС ДУ
решения ЛОС ДУ  и
и 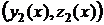 называются фундаментальной системой решений системы уравнений (4.5).
называются фундаментальной системой решений системы уравнений (4.5).
Теорема 2. Если семейство функций  и
и 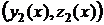 образует фундаментальную систему решений ЛОС ДУ (4.5), то их линейная комбинация
образует фундаментальную систему решений ЛОС ДУ (4.5), то их линейная комбинация

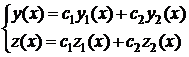 , (4.9)
, (4.9)
где 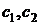 – произвольные постоянные, даёт общее решение системы (4.5).
– произвольные постоянные, даёт общее решение системы (4.5).
Доказательство.
1. Равенства (4.9), согласно следствию из свойств решений ЛОС ДУ, определяют решение системы уравнений (4.5).
2. Докажем, что равенства (4.9) определяют общее решение (4.5), для этого докажем, что каковы бы ни были начальные условия задачи Коши 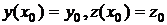 , всегда найдутся значения постоянных
, всегда найдутся значения постоянных  такие, что выделенное из общего частное решение ЛОС ДУ
такие, что выделенное из общего частное решение ЛОС ДУ

будет удовлетворять этим условиям.
Для этого подставим в равенства (4.9) начальные условия, получим:
 (4.10)
(4.10)
Определителем этой алгебраической системы линейных уравнений является определитель Вронского  :
:
 ,
,
который, согласно теореме 1, не равен нулю. Следовательно, система уравнений (4.10) имеет решение  и притом единственное.
и притом единственное.
4.4. ЛОС ДУ с постоянными коэффициентами
Линейная однородная система дифференциальных уравнений с постоянными коэффициентами имеет вид
 (4.11)
(4.11)
где  – некоторые постоянные. Система (4.11) имеет фундаментальную систему решений, состоящую из элементарных функций. Основным методом построения фундаментальной системы решений для системы (4.11) является метод Эйлера. Согласно этому методу, решение ЛОС ДУ ищется в виде
– некоторые постоянные. Система (4.11) имеет фундаментальную систему решений, состоящую из элементарных функций. Основным методом построения фундаментальной системы решений для системы (4.11) является метод Эйлера. Согласно этому методу, решение ЛОС ДУ ищется в виде  .
.
Продифференцируем обе функции по x и подставим в уравнения системы (4.11):
 .
.
Сокращаем оба уравнения системы на  :
:
 (4.12)
(4.12)
Так как  – некоторые постоянные числа, подлежащие определению, среди которых хотя бы одно отлично от нуля, то определитель системы (4.12) должен быть равен нулю
– некоторые постоянные числа, подлежащие определению, среди которых хотя бы одно отлично от нуля, то определитель системы (4.12) должен быть равен нулю
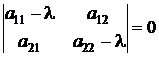 . (4.13)
. (4.13)
Уравнение (4.13) называется характеристическим уравнением, а его корни – характеристическими числами системы (4.11). Каждому из корней характеристического уравнения соответствует хотя бы одно частное решение указанного выше вида. Различают три случая.
1. Оба корня характеристического уравнения вещественны и различны:  ℝ,
ℝ,  . Подставляем
. Подставляем  в одно из уравнений системы (4.12), например, в первое уравнение:
в одно из уравнений системы (4.12), например, в первое уравнение:  Из него с точностью до константы определяем
Из него с точностью до константы определяем 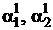 , откуда получаем первое решение ЛОС ДУ:
, откуда получаем первое решение ЛОС ДУ:
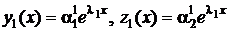 .
.
То же самое проделываем со вторым корнем характеристического уравнения 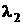 и в результате получаем второе, линейно независимое на
и в результате получаем второе, линейно независимое на  с первым, решение ЛОС ДУ:
с первым, решение ЛОС ДУ:
 .
.
Следовательно, согласно теореме 2раздела4.3. общим решением системы (4.11) будет следующее семейство функций:
 ,
,
 .
.
2. Если 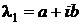 – корень характеристического уравнения, то
– корень характеристического уравнения, то  . Подставляем
. Подставляем  в одно из двух уравнений системы (4.12) и с точностью до постоянной получаем
в одно из двух уравнений системы (4.12) и с точностью до постоянной получаем  . Теперь составляем первое решение системы (4.11):
. Теперь составляем первое решение системы (4.11):

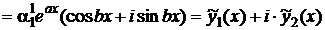 ,
,
 .
.
Отделив вещественную и мнимую части, получим два вещественных линейно независимых частных решения системы (4.11), соответствующих корню  . Решения, соответствующие корню
. Решения, соответствующие корню  , будут линейно зависимы с решениями, соответствующими корню
, будут линейно зависимы с решениями, соответствующими корню  .
.
Итак, общее решение ЛОС ДУ в этом случае примет вид:
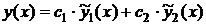
 .
.
3.  . В случае кратного корня характеристического уравнения необходимо представить общее решение системы уравнений (4.11) в следующем виде:
. В случае кратного корня характеристического уравнения необходимо представить общее решение системы уравнений (4.11) в следующем виде:
 ,
,
где 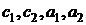 – постоянные числа, причём
– постоянные числа, причём  и
и  должны быть выражены через
должны быть выражены через 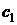 и
и  .
.
Пример. Найти общее решение системы:
 .
.
Решение: Будем искать решение в виде  . Характеристическое уравнение:
. Характеристическое уравнение:
 .
.
Его корни:  . Следовательно,
. Следовательно,
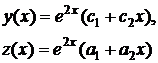 .
.
Продифференцируем y (x) и подставим  в первое уравнение исходной системы:
в первое уравнение исходной системы:
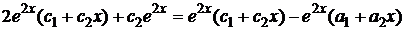 .
.
Отсюда после сокращения на  получаем
получаем
 .
.
Приравняем в этом тождестве множители при одинаковых степенях x. В результате получим:  .
.
Итак, общее решение заданной системы уравнений имеет вид:

где 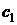 и
и  – произвольные постоянные.
– произвольные постоянные.
4.5. Линейные неоднородные системы
дифференциальных уравнений (ЛНС ДУ)
Определение 1. Линейной неоднородной системой дифференциальных уравнений (ЛНС ДУ) называется система уравнений следующего вида
 (4.14)
(4.14)
где  – заданные непрерывные на интервале
– заданные непрерывные на интервале  функции.
функции.
Теорема 1. Общее решение ЛНС ДУ (4.14) представляет собой сумму общего решения соответствующей ЛОС ДУ (4.5) и какого-либо частного решения системы (4.14):
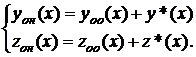 (4.15)
(4.15)
Доказательство.
1. Прежде всего докажем, что система уравнений (4.15) определяет решение ЛНС ДУ (4.14). Для этого, подставим выражение (4.15) в первое уравнение системы (4.14) и покажем, что в результате получится тождество.
 ,
,
т.е. имеем  .
.
Аналогичный вывод имеет место и для второго уравнения системы (4.14).
2. Во второй части доказательства докажем, что выражения (4.15) дают общее решение ЛНС. Для этого надо показать, что всегда найдутся числа 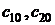 такие, что выделенное из семейства (4.15) частное решение будет удовлетворять начальным условиям
такие, что выделенное из семейства (4.15) частное решение будет удовлетворять начальным условиям
 (4.16)
(4.16)
Согласно теореме 2раздела4.3. выражения (4.15) можно переписать в виде:
 (4.17)
(4.17)
где 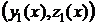 и
и  образуют фундаментальную систему решений ЛОС ДУ. Подставим в систему (4.17) начальные условия:
образуют фундаментальную систему решений ЛОС ДУ. Подставим в систему (4.17) начальные условия:

или
 (4.18)
(4.18)
Определитель этой системы уравнений есть определитель Вронского
 ,
,
но согласно теореме 1 пункта 4.3.  , следовательно, система уравнений (4.18) имеет решение и притом единственное:
, следовательно, система уравнений (4.18) имеет решение и притом единственное:  .
.
Теорема доказана.
4.6. Метод вариации произвольных постоянных
Применим метод вариации постоянных, описанный ранее, для решения линейной неоднородной системы дифференциальных уравнений (4.14).
Общее решение соответствующей однородной системы (4.5) задаётся парой выражений:
 ,
,
где 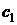 и
и  – произвольные постоянные. Будем искать решение системы (4.14) в виде
– произвольные постоянные. Будем искать решение системы (4.14) в виде
 (4.19)
(4.19)
где 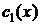 и
и  – функции, подлежащие определению.
– функции, подлежащие определению.
Подставим выражения (4.19) в систему (4.14), получим:
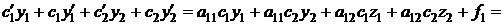
 .
.
Откуда получаем 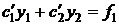 .
.
Аналогично получаем второе уравнение для функций  :
:
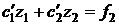 .
.
Итак, для производных  имеем систему уравнений
имеем систему уравнений
 . (4.20)
. (4.20)
Определитель последней системы есть определитель Вронского для фундаментальной системы решений системы (4.5), который не обращается в нуль ни в одной точке интервала  . Поэтому, решая систему (4.20), однозначно определяются
. Поэтому, решая систему (4.20), однозначно определяются  и
и 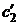 :
:
 и
и 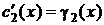 .
.
Интегрируя эти выражения и подставляя результат в систему (4.19), получим ответ.