Задачи на тему «Закон сохранения энергии»

1. Сна­ряд мас­сой 4 кг, ле­тя­щий со ско­ро­стью 400 м/с, раз­ры­ва­ет­ся на две рав­ные части, одна из ко­то­рых летит в на­прав­ле­нии дви­же­ния сна­ря­да, а дру­гая — в про­ти­во­по­лож­ную сто­ро­ну. В мо­мент раз­ры­ва сум­мар­ная ки­не­ти­че­ская энер­гия оскол­ков уве­ли­чи­лась на ве­ли­чи­ну 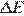. Ско­рость оскол­ка, ле­тя­ще­го по на­прав­ле­нию дви­же­ния сна­ря­да, равна 900 м/с. Най­ди­те .

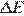2. Кусок пла­сти­ли­на стал­ки­ва­ет­ся со сколь­зя­щим нав­стре­чу по го­ри­зон­таль­ной по­верх­но­сти стола брус­ком и при­ли­па­ет к нему. Ско­ро­сти пла­сти­ли­на и брус­ка перед уда­ром на­прав­ле­ны вза­им­но про­ти­во­по­лож­но и равны и . Масса брус­ка в 4 раза боль­ше массы пла­сти­ли­на. К мо­мен­ту, когда ско­рость слип­ших­ся брус­ка и пла­сти­ли­на умень­ши­лась в 2 раза, они пе­ре­ме­сти­лись на 0,22 м. Опре­де­ли­те ко­эф­фи­ци­ент тре­ния 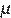брус­ка о по­верх­ность стола.

3. Бру­сок мас­сой 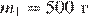со­скаль­зы­ва­ет по на­клон­ной плос­ко­сти с вы­со­ты h и, дви­га­ясь по го­ри­зон­таль­ной по­верх­но­сти, стал­ки­ва­ет­ся с не­по­движ­ным брус­ком мас­сой . В ре­зуль­та­те аб­со­лют­но не­упру­го­го со­уда­ре­ния общая ки­не­ти­че­ская энер­гия брус­ков ста­но­вит­ся рав­ной 2,5 Дж. Опре­де­ли­те вы­со­ту на­клон­ной плос­ко­сти h. Тре­ни­ем при дви­же­нии пре­не­бречь. Счи­тать, что на­клон­ная плос­кость плав­но пе­ре­хо­дит в го­ри­зон­таль­ную.

4. Ма­лень­кий шарик па­да­ет свер­ху на на­клон­ную плос­кость и упру­го от­ра­жа­ет­ся от неё. Угол на­кло­на плос­ко­сти к го­ри­зон­ту равен 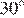. На какое рас­сто­я­ние по го­ри­зон­та­ли пе­ре­ме­ща­ет­ся шарик между пер­вым и вто­рым уда­ра­ми о плос­кость? Ско­рость ша­ри­ка не­по­сред­ствен­но перед пер­вым уда­ром на­прав­ле­на вер­ти­каль­но вниз и равна 1 м/с.

5. На глад­кой го­ри­зон­таль­ной по­верх­но­сти стола по­ко­ит­ся горка с двумя вер­ши­на­ми, вы­со­ты ко­то­рых h и 4 h (см. ри­су­нок). На пра­вой вер­ши­не горки на­хо­дит­ся шайба. Масса горки в 8 раз боль­ше массы шайбы. От не­зна­чи­тель­но­го толч­ка шайба и горка при­хо­дят в дви­же­ние, причём шайба дви­жет­ся влево, не от­ры­ва­ясь от глад­кой по­верх­но­сти горки, а по­сту­па­тель­но дви­жу­ща­я­ся горка не от­ры­ва­ет­ся от стола. Най­ди­те ско­рость шайбы на левой вер­ши­не горки.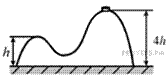

6. Го­ри­зон­таль­ная по­верх­ность раз­де­ле­на на две части: глад­кую и ше­ро­хо­ва­тую. На гра­ни­це этих ча­стей на­хо­дит­ся кубик мас­сой m = 100 г. Со сто­ро­ны глад­кой части на него по го­ри­зон­та­ли на­ле­та­ет ме­тал­ли­че­ский шар мас­сой M = 300 г, дви­жу­щий­ся со ско­ро­стью v ₀ = 2 м/с. Опре­де­ли­те рас­сто­я­ние L, ко­то­рое пройдёт кубик до оста­нов­ки после аб­со­лют­но упру­го­го цен­траль­но­го со­уда­ре­ния с шаром. Ко­эф­фи­ци­ент тре­ния ку­би­ка о по­верх­ность μ = 0,3.

7. По глад­кой го­ри­зон­таль­ной плос­ко­сти сколь­зит шарик мас­сой m = 2 кг со ско­ро­стью v = 2 м/с. Он ис­пы­ты­ва­ет ло­бо­вое аб­со­лют­но упру­гое столк­но­ве­ние с дру­гим ша­ри­ком мас­сой M = 2,5 кг, ко­то­рый до столк­но­ве­ния по­ко­ил­ся (см. рис.). После этого вто­рой шарик уда­ря­ет­ся о мас­сив­ный кусок пла­сти­ли­на, при­кле­ен­но­го к плос­ко­сти, и при­ли­па­ет к нему. Най­ди­те мо­дуль им­пуль­са, ко­то­рый вто­рой шарик пе­ре­дал куску пла­сти­ли­на.

8. Два ша­ри­ка, массы ко­то­рых m = 0,1 кг и М = 0,2 кг, висят, со­при­ка­са­ясь, на вер­ти­каль­ных нитях оди­на­ко­вой длины l (см. ри­су­нок). Левый шарик от­кло­ня­ют на угол 90° и от­пус­ка­ют с на­чаль­ной ско­ро­стью, рав­ной нулю. В ре­зуль­та­те аб­со­лют­но не­упру­го­го удара ша­ри­ков вы­де­ля­ет­ся ко­ли­че­ство теп­ло­ты Q = 1 Дж. Опре­де­ли­те длину нитей l.

9. Бру­сок мас­сой m ₁ = 500 г со­скаль­зы­ва­ет по на­клон­ной плос­ко­сти с не­ко­то­рой вы­со­ты h и, дви­га­ясь по го­ри­зон­таль­ной по­верх­но­сти, стал­ки­ва­ет­ся с не­по­движ­ным брус­ком мас­сой m ₂ = 300 г. Счи­тая столк­но­ве­ние аб­со­лют­но не­упру­гим, опре­де­ли­те вы­со­ту h, если общая ки­не­ти­че­ская энер­гия брус­ков после столк­но­ве­ния равна 2,5 Дж. Тре­ни­ем при дви­же­нии пре­не­бречь. Счи­тать, что на­клон­ная плос­кость плав­но пе­ре­хо­дит в го­ри­зон­таль­ную.

10. Струя воды круг­ло­го се­че­ния ра­ди­у­сом r ₀ = 1 см на­чи­на­ет бить из шлан­га вверх со ско­ро­стью v ₀ = 20 м/с. Най­ди­те ра­ди­ус струи r на вы­со­те h = 16 м по вер­ти­ка­ли от конца шлан­га. Тре­ни­ем и си­ла­ми по­верх­ност­но­го на­тя­же­ния пре­не­бречь, счи­тать ско­рость дви­же­ния ча­стиц воды по вер­ти­ка­ли в любом по­пе­реч­ном се­че­нии струи оди­на­ко­вой для дан­но­го се­че­ния, а сами ча­сти­цы — на­хо­дя­щи­ми­ся в со­сто­я­нии сво­бод­но­го па­де­ния в поле силы тя­же­сти.

За­да­ние 28 № 7369

11. К по­тол­ку на двух оди­на­ко­вых лёгких пру­жи­нах общей жёстко­стью k = 400 Н/м под­ве­ше­на чашка мас­сой m = 500 г. С вы­со­ты h = 10 см в чашку па­да­ет и при­ли­па­ет к ней груз такой же мас­сой m (см. рис.). На какое мак­си­маль­ное рас­сто­я­ние H после этого опу­стит­ся чашка от­но­си­тель­но сво­е­го ис­ход­но­го по­ло­же­ния? По­те­ря­ми ме­ха­ни­че­ской энер­гии пре­не­бречь.

За­да­ние 28 № 7642

12. Ма­лень­кий шарик мас­сой кг под­ве­шен на лёгкой не­рас­тя­жи­мой нити дли­ной 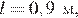ко­то­рая раз­ры­ва­ет­ся при силе на­тя­же­ния Шарик отведён от по­ло­же­ния рав­но­ве­сия (оно по­ка­за­но на ри­сун­ке пунк­ти­ром) и от­пу­щен. Когда шарик про­хо­дит по­ло­же­ние рав­но­ве­сия, нить об­ры­ва­ет­ся, и шарик тут же аб­со­лют­но не­упру­го стал­ки­ва­ет­ся с брус­ком мас­сой ле­жа­щим не­по­движ­но на глад­кой го­ри­зон­таль­ной по­верх­но­сти стола. Ка­ко­ва ско­рость u брус­ка после удара? Счи­тать, что бру­сок после удара дви­жет­ся по­сту­па­тель­но.