Вариант №1
1. Дан простой статистический ряд. Записать интервальный вариационный ряд, выбрав соответствующую величину интервала. Построить гистограмму частот и полигон относительных частот, а также вычислить среднее значение и дисперсию.
| № | ||||||||||
| X | 3,37 | 3,45 | 3,86 | 3,63 | 3,74 | 3,75 | 3,67 | 3,99 | 4,11 | 3,77 |
| № | ||||||||||
| X | 3,98 | 4,18 | 4,45 | 4,11 | 4,34 | 4,04 | 3,79 | 3,88 | 4,27 | 4,15 |
| № | ||||||||||
| X | 4,06 | 4,35 | 4,38 | 4,59 | 4,26 | 3,89 | 3,55 | 3,79 | 4,21 | 4,09 |
| № | ||||||||||
| X | 3,84 | 3,94 | 3,81 | 3,90 | 3,67 | 3,92 | 3,36 | 3,79 | 3,64 | 3,75 |
| № | ||||||||||
| X | 3,97 | 4,15 | 4,51 | 4,55 | 4,36 | 4,06 | 3,78 | 3,87 | 3,55 | 3,67 |
2. Из генеральной совокупности извлечена выборка, которая представлена в виде интервального вариационного ряда. а) Предполагая, что генеральная совокупность имеет нормальное распределение, построить доверительный интервал для математического ожидания и дисперсии с доверительной вероятностью g=0,95. б) Вычислить коэффициенты асимметрии и эксцесса и сделать соответствующие предположения о виде функции распределения генеральной совокупности. в) Используя критерий Пирсона, проверить гипотезу о нормальности распределения генеральной совокупности при уровне значимости a=0,05.
| x | 3,0-3,6 | 3,6-4,2 | 4,2-4,8 | 4,8-5,4 | 5,4-6,0 | 6,0-6,6 | 6,6-7,2 |
| n |
3. Задана корреляционная таблица величин X и Y. а) Вычислить коэффициент корреляции r xy Сделать выводы о связи между X и Y. б) Найти уравнения линейной регрессии X на Y и Y на X, а также построить их графики.
| X Y | 1,15-1,22 | 1,22-1,29 | 1,29-1,36 | 1,36-1,43 | 1,43-1,50 | 1,50-1,57 | 1,57-1,64 | 1,64-1,71 | 1,71-1,78 | ny |
| 74,5-81,5 | ||||||||||
| 81,5-88,5 | ||||||||||
| 88,5-95,5 | ||||||||||
| 95,5-102,5 | ||||||||||
| 102,5-109,5 | ||||||||||
| 109,5-116,5 | ||||||||||
| 116,5-123,5 | ||||||||||
| 123,5-130,5 | ||||||||||
| 130,5-137,5 | ||||||||||
| nx |
4. Методом наименьших квадратов подобрать функцию 
по табличным данным и сделать чертеж.
| x | |||||||
| y |
5. В таблице приводится зависимость розничного товарооборота (Z, млн. р.) для различных регионов от средней численности населения (X, тыс. р.) и среднегодового дохода (Y, тыс. р.), в расчете на одного человека.
| Z | X | Y |
На основании данных таблицы найти уравнение линейной регрессии Z от X и Y, объяснить его сущность, вычислить коэффициент парной корреляции, частные коэффициенты корреляции, совокупный коэффициент множественной корреляции. Сделать экономический анализ.
Типовой расчет
Элементы математической статистики
Вариант №2
1. Дан простой статистический ряд. Записать интервальный вариационный ряд, выбрав соответствующую величину интервала. Построить гистограмму частот и полигон относительных частот, а также вычислить среднее значение и дисперсию.
| № | ||||||||||
| X | ||||||||||
| № | ||||||||||
| X | ||||||||||
| № | ||||||||||
| X | ||||||||||
| № | ||||||||||
| X | ||||||||||
| № | ||||||||||
| X |
2. Из генеральной совокупности извлечена выборка, которая представлена в виде интервального вариационного ряда. а) Предполагая, что генеральная совокупность имеет нормальное распределение, построить доверительный интервал для математического ожидания и дисперсии с доверительной вероятностью g=0,95. б) Вычислить коэффициенты асимметрии и эксцесса и сделать соответствующие предположения о виде функции распределения генеральной совокупности. в) Используя критерий Пирсона, проверить гипотезу о нормальности распределения генеральной совокупности при уровне значимости a=0,05.
| x | 190-200 | 200-210 | 210-220 | 220-230 | 230-240 | 240-250 |
| n |
3. Задана корреляционная таблица величин X и Y. а) Вычислить коэффициент корреляции r xy Сделать выводы о связи между X и Y. б) Найти уравнения линейной регрессии X на Y и Y на X, а также построить их графики.
| X Y | 2,73-2,82 | 2,82-2,91 | 2,91-3,00 | 3,00-3,09 | 3,09-3,18 | 3,18-3,27 | 3,27-3,36 | 3,36-3,45 | 3,45-3,54 | ny |
| 512-525 | ||||||||||
| 525-538 | ||||||||||
| 538-551 | ||||||||||
| 551-564 | ||||||||||
| 564-577 | ||||||||||
| 577-590 | ||||||||||
| 590-603 | ||||||||||
| 603-616 | ||||||||||
| 616-629 | ||||||||||
| nx |
4. Методом наименьших квадратов подобрать функцию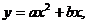 
по табличным данным и сделать чертеж.
| x | |||||||
| y | 7,4 | 8,4 | 9,1 | 9,4 | 9,5 | 9,5 | 9,4 |
5. В таблице приводятся выборочные данные зависимости урожайности зерновых (Z, ц/га.) от расхода органических и минеральных удобрений на 1 га (X, млн. р.) и расхода семян на 1 га (Y, тыс. р.).
| Z | X | Y |
| 18,3 | ||
| 19,5 | ||
| 20,2 | ||
| 22,0 | ||
| 22,5 | ||
| 23,5 | ||
| 23,5 | ||
| 23,8 | ||
| 24,0 | ||
| 24,7 | ||
| 24,9 |
На основании данных таблицы найти уравнение линейной регрессии Z от X и Y, объяснить его сущность, вычислить коэффициент парной корреляции, частные коэффициенты корреляции, совокупный коэффициент множественной корреляции. Сделать экономический анализ.
Типовой расчет
для экономических специальностей по теме
Элементы математической статистики
Вариант №3
1. Дан простой статистический ряд. Записать интервальный вариационный ряд, выбрав соответствующую величину интервала. Построить гистограмму частот и полигон относительных частот, а также вычислить среднее значение и дисперсию.
| № | ||||||||||
| X | 15,4 | 16,5 | 17,1 | 21,3 | 19,6 | 24,7 | 29,1 | 30,2 | 32,5 | 36,7 |
| № | ||||||||||
| X | 24,0 | 37,3 | 39,5 | 41,2 | 43,3 | 47,5 | 42,4 | 46,5 | 42,4 | 37,5 |
| № | ||||||||||
| X | 33,3 | 34,4 | 31,9 | 27,8 | 25,0 | 24,1 | 22,1 | 19,9 | 23,7 | 28,1 |
| № | ||||||||||
| X | 32,8 | 29,5 | 36,5 | 40,1 | 39,5 | 38,1 | 33,5 | 30,5 | 31,1 | 29,1 |
| № | ||||||||||
| X | 20,9 | 27,7 | 26,1 | 31,5 | 34,1 | 24,0 | 34,8 | 34,1 | 34,3 | 28,1 |
2. Из генеральной совокупности извлечена выборка, которая представлена в виде интервального вариационного ряда. а) Предполагая, что генеральная совокупность имеет нормальное распределение, построить доверительные интервалы для математического ожидания и дисперсии с доверительной вероятностью g=0,95. б) Вычислить коэффициенты асимметрии и эксцесса и сделать соответствующие предположения о виде функции распределения генеральной совокупности. в) Используя критерий Пирсона, проверить гипотезу о нормальности распределения генеральной совокупности при уровне значимости a=0,05.
| x | 29-32 | 32-35 | 35-38 | 38-41 | 41-44 | 44-47 | 47-50 |
| n |
3. Задана корреляционная таблица величин X и Y. а) Вычислить коэффициент корреляции r xy Сделать выводы о связи между X и Y. б) Найти уравнения линейной регрессии X на Y и Y на X, а также построить их графики.
| X Y | 4,24-4,35 | 4,35-4,46 | 4,46-4,57 | 4,57-4,68 | 4,68-4,79 | 4,79-4,90 | 4,90-5,01 | 5,01-5,12 | 5,12-5,23 | ny |
| 21,3-22,0 | ||||||||||
| 22,0-22,7 | ||||||||||
| 22,7-23,4 | ||||||||||
| 23,4-24,1 | ||||||||||
| 24,1-24,8 | ||||||||||
| 24,8-25,5 | ||||||||||
| 25,5-26,2 | ||||||||||
| 26,2-26,9 | ||||||||||
| 26,9-27,6 | ||||||||||
| nx |
4. Методом наименьших квадратов подобрать функцию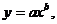 
по табличным данным и сделать чертеж.
| x | |||||
| y | 7,1 | 62,1 |
5. В таблице приводится зависимость розничного товарооборота (Z, млн. р.) для различных регионов от средней численности населения (X, тыс. р.) и среднегодового дохода (Y, тыс. р.), в расчете на одного человека.
| Z | X | Y |
На основании данных таблицы найти уравнение линейной регрессии Z от X и Y, объяснить его сущность, вычислить коэффициент парной корреляции, частные коэффициенты корреляции, совокупный коэффициент множественной корреляции. Сделать экономический анализ.
Типовой расчет
Элементы математической статистики
Вариант №4
1. Дан простой статистический ряд. Записать интервальный вариационный ряд, выбрав соответствующую величину интервала. Построить гистограмму частот и полигон относительных частот, а также вычислить среднее значение и дисперсию.
| № | ||||||||||
| X | ||||||||||
| № | ||||||||||
| X | ||||||||||
| № | ||||||||||
| X | ||||||||||
| № | ||||||||||
| X | ||||||||||
| № | ||||||||||
| X |
2. Из генеральной совокупности извлечена выборка, которая представлена в виде интервального вариационного ряда. а) Предполагая, что генеральная совокупность имеет нормальное распределение, построить доверительные интервалы для математического ожидания и дисперсии с доверительной вероятностью g=0,95. б) Вычислить коэффициенты асимметрии и эксцесса и сделать соответствующие предположения о виде функции распределения генеральной совокупности. в) Используя критерий Пирсона, проверить гипотезу о нормальности распределения генеральной совокупности при уровне значимости a=0,05.
| x | 5,0-5,4 | 5,4-5,8 | 5,8-6,2 | 6,2-6,6 | 6,6-7,0 | 7,0-7,4 | 7,4-7,8 |
| n |
3. Задана корреляционная таблица величин X и Y. а) Вычислить коэффициент корреляции r xy сделать выводы о связи между X и Y. б) Найти уравнения линейной регрессии X на Y и Y на X, а также построить их графики.
| X Y | 3,35-3,42 | 3,42-3,49 | 3,49-3,56 | 3,56-3,63 | 3,63-3,70 | 3,70-3,77 | 3,77-3,84 | 3,84-3,91 | 3,91-3,98 | ny |
| 54,5-61,5 | ||||||||||
| 61,5-68,5 | ||||||||||
| 68,5-75,5 | ||||||||||
| 75,5-82,5 | ||||||||||
| 82,5-89,5 | ||||||||||
| 89,5-96,5 | ||||||||||
| 96,5-103,5 | ||||||||||
| 103,5-110,5 | ||||||||||
| 110,5-117,5 | ||||||||||
| nx |
4. Методом наименьших квадратов подобрать функцию 
по табличным данным и сделать чертеж.
| x | |||||||
| y |
5. В таблице приводятся выборочные данные зависимости урожайности зерновых (Z, ц/га.) от расхода органических и минеральных удобрений на 1 га (X, млн. р.) и расхода семян на 1 га (Y, тыс. р.).
| Z | X | Y |
| 18,3 | ||
| 19,5 | ||
| 20,2 | ||
| 22,0 | ||
| 22,5 | ||
| 23,5 | ||
| 23,5 | ||
| 23,8 | ||
| 24,0 | ||
| 24,7 | ||
| 24,9 |
На основании данных таблицы найти уравнение линейной регрессии Z от X и Y, объяснить его сущность, вычислить коэффициент парной корреляции, частные коэффициенты корреляции, совокупный коэффициент множественной корреляции. Сделать экономический анализ.
Типовой расчет
Элементы математической статистики
Вариант №5
1. Дан простой статистический ряд. Записать интервальный вариационный ряд, выбрав соответствующую величину интервала. Построить гистограмму частот и полигон относительных частот, а также вычислить среднее значение и дисперсию.
| № | ||||||||||
| X | 4,18 | 4,14 | 4,19 | 4,25 | 4,33 | 4,39 | 4,41 | 4,54 | 4,32 | 4,49 |
| № | ||||||||||
| X | 4,54 | 4,59 | 4,66 | 4,72 | 4,75 | 4,87 | 4,99 | 4,81 | 4,74 | 4,60 |
| № | ||||||||||
| X | 4,55 | 4,54 | 4,48 | 4,40 | 4,39 | 4,35 | 4,21 | 4,11 | 4,34 | 4,38 |
| № | ||||||||||
| X | 4,43 | 4,51 | 4,57 | 4,62 | 4,50 | 4,59 | 4,64 | 4,51 | 4,44 | 4,47 |
| № |
2. Из генеральной совокупности извлечена выборка, которая представлена в виде интервального вариационного ряда. а) Предполагая, что генеральная совокупность имеет нормальное распределение, построить доверительные интервалы для математического ожидания и дисперсии с доверительной вероятностью g=0,95. б) Вычислить коэффициенты асимметрии и эксцесса и сделать соответствующие предположения о виде функции распределения генеральной совокупности. в) Используя критерий Пирсона, проверить гипотезу о нормальности распределения генеральной совокупности при уровне значимости a=0,05.
| x | 90-110 | 110-130 | 130-150 | 150-170 | 170-190 | 190-210 |
| n |
3. Задана корреляционная таблица величин X и Y. а) Вычислить коэффициент корреляции r xy сделать выводы о связи между X и Y. б) Найти уравнения линейной регрессии X на Y и Y на X, а также построить их графики.
| X Y | 5,73-5,82 | 5,82-5,91 | 5,91-6,00 | 6,00-6,09 | 6,09-6,18 | 6,18-6,27 | 6,27-6,36 | 6,36-6,45 | 6,45-6,54 | ny |
| 312-325 | ||||||||||
| 325-338 | ||||||||||
| 338-351 | ||||||||||
| 351-364 | ||||||||||
| 364-377 | ||||||||||
| 377-390 | ||||||||||
| 390-403 | ||||||||||
| 403-426 | ||||||||||
| 426-439 | ||||||||||
| nx |
4. Методом наименьших квадратов подобрать функцию 
по табличным данным и сделать чертеж.
| x | |||||||
| y | 3,5 | 4,5 | 7,1 | 9,4 | 10,8 | 12,1 | 15,9 |
5. В таблице приводится зависимость розничного товарооборота (Z, млн. р.) для различных регионов от средней численности населения (X, тыс. р.) и среднегодового дохода (Y, тыс. р.), в расчете на одного человека.
| Z | X | Y |
На основании данных таблицы найти уравнение линейной регрессии Z от X и Y, объяснить его сущность, вычислить коэффициент парной корреляции, частные коэффициенты корреляции, совокупный коэффициент множественной корреляции. Сделать экономический анализ.
Типовой расчет
Элементы математической статистики
Вариант №6
1. Дан простой статистический ряд. Записать интервальный вариационный ряд, выбрав соответствующую величину интервала. Построить гистограмму частот и полигон относительных частот, а также вычислить среднее значение и дисперсию.
| № | ||||||||||
| X | ||||||||||
| № | ||||||||||
| X | ||||||||||
| № | ||||||||||
| X | ||||||||||
| № | ||||||||||
| X | ||||||||||
| № | ||||||||||
| X |
2. Из генеральной совокупности извлечена выборка, которая представлена в виде интервального вариационного ряда. а) Предполагая, что генеральная совокупность имеет нормальное распределение, построить доверительные интервалы для математического ожидания и дисперсии с доверительной вероятностью g=0,95. б) Вычислить коэффициенты асимметрии и эксцесса и сделать соответствующие предположения о виде функции распределения генеральной совокупности. в) Используя критерий Пирсона, проверить гипотезу о нормальности распределения генеральной совокупности при уровне значимости a=0,05.
| x | 20-32 | 32-44 | 44-56 | 56-68 | 68-80 | 80-92 | 92-104 |
| n |
3. Задана корреляционная таблица величин X и Y. а) Вычислить коэффициент корреляции r xy сделать выводы о связи между X и Y. б) Найти уравнения линейной регрессии X на Y и Y на X, а также построить их графики.
| X Y | 6,24-6,35 | 6,35-6,46 | 6,46-6,57 | 6,57-6,68 | 6,68-6,79 | 6,79-6,90 | 6,90-7,01 | 7,01-7,12 | 7,12-7,23 | ny |
| 31,3-32,0 | ||||||||||
| 32,0-32,7 | ||||||||||
| 32,7-33,4 | ||||||||||
| 33,4-34,1 | ||||||||||
| 34,1-34,8 | ||||||||||
| 34,8-35,5 | ||||||||||
| 35,5-36,2 | ||||||||||
| 36,2-36,9 | ||||||||||
| 36,9-37,6 | ||||||||||
| nx |
4. Методом наименьших квадратов подобрать функцию 
по табличным данным и сделать чертеж.
| x | ||||||||
| y | 9,1 | 5,3 | 4,11 | 2,83 | 2,11 | 1,62 | 1,41 | 1,3 |
5. В таблице приводятся выборочные данные зависимости урожайности зерновых (Z, ц/га.) от расхода органических и минеральных удобрений на 1 га (X, млн. р.) и расхода семян на 1 га
(Y, тыс. р.).
| Z | X | Y |
| 25,3 | ||
| 26,1 | ||
| 26,5 | ||
| 27,2 | ||
| 27,8 | ||
| 28,0 | ||
| 28,4 | ||
| 29,5 | ||
| 29,8 | ||
| 30,2 | ||
| 31,5 |
На основании данных таблицы найти уравнение линейной регрессии Z от X и Y, объяснить его сущность, вычислить коэффициент парной корреляции, частные коэффициенты корреляции, совокупный коэффициент множественной корреляции. Сделать экономический анализ.
Типовой расчет
Элементы математической статистики
Вариант №7
1. Дан простой статистический ряд. Записать интервальный вариационный ряд, выбрав соответствующую величину интервала. Построить гистограмму частот и полигон относительных частот, а также вычислить среднее значение и дисперсию.
| № | ||||||||||
| X | 43,4 | 41,9 | 42,7 | 40,9 | 41,1 | 43,1 | 44,2 | 44,9 | 43,5 | 42,1 |
| № | ||||||||||
| X | 42,3 | 41,4 | 41,9 | 40,7 | 41,4 | 42,1 | 39,3 | 38,6 | 39,7 | 40,7 |
| № | ||||||||||
| X | 41,0 | 40,9 | 41,6 | 42,0 | 41,9 | 41,8 | 41,7 | 42,1 | 43,9 | 44,2 |
| № | ||||||||||
| X | 44,8 | 42,0 | 43,4 | 42,7 | 41,5 | 42,2 | 41,6 | 41,3 | 40,7 | 43,0 |
| № | ||||||||||
| X | 41,3 | 43,5 | 42,8 | 44,6 | 41,6 | 38,8 | 41,7 | 42,2 | 39,4 | 38,9 |
2. Из генеральной совокупности извлечена выборка, которая представлена в виде интервального вариационного ряда. а) Предполагая, что генеральная совокупность имеет нормальное распределение, построить доверительные интервалы для математического ожидания и дисперсии с доверительной вероятностью g=0,95. б) Вычислить коэффициенты асимметрии и эксцесса и сделать соответствующие предположения о виде функции распределения генеральной совокупности. в) Используя критерий Пирсона, проверить гипотезу о нормальности распределения генеральной совокупности при уровне значимости a=0,05.
| x | 7,0-7,6 | 7,6-8,2 | 8,2-8,8 | 8,8-9,4 | 9,4-10,0 | 10,0-10,6 | 10,6-11,2 |
| n |
3. Задана корреляционная таблица величин X и Y. а) Вычислить коэффициент корреляции r xy сделать выводы о связи между X и Y. б) Найти уравнения линейной регрессии X на Y и Y на X, а также построить их графики.
| X Y | 9,15-9,22 | 9,22-9,29 | 9,29-9,36 | 9,36-9,43 | 9,43-9,50 | 9,50-9,57 | 9,57-9,64 | 9,64-9,71 | 9,71-9,78 | ny |
| 94,5-101,5 | ||||||||||
| 101,5-108,5 | ||||||||||
| 108,5-115,5 | ||||||||||
| 115,5-122,5 | ||||||||||
| 122,5-129,5 | ||||||||||
| 129,5-136,5 | ||||||||||
| 136,5-143,5 | ||||||||||
| 143,5-150,5 | ||||||||||
| 150,5-157,5 | ||||||||||
| nx |
4. Методом наименьших квадратов подобрать функцию по табличным данным и сделать чертеж.
| x | ||||||
| y |
5. В таблице приводится зависимость розничного товарооборота (Z, млн. р.) для различных регионов от средней численности населения (X, тыс. р.) и среднегодового дохода (Y, тыс. р.), в расчете на одного человека.
| Z | X | Y |
На основании данных таблицы найти уравнение линейной регрессии Z от X и Y, объяснить его сущнос