Функция операторного сопротивления двухполюсника Z(p), по которой можно построить соответствующую цепь называется физически реализуемой. Удобнее всего представить исследуемый двухполюсник в виде одной из канонических схем. Значения переменного р, соответствующего корням многочлена в числителе, обращают Z(p) в нуль и называются нулями функции Z(p). Корни многочлена, находящегося в знаменателе дроби, являются полюсами функции. Определив нули и полюсы функции операторного сопротивления двухполюсника Z(p), можно построить полюсно-нулевое изображение на плоскости комплексного переменного р. Нули и полюсы физически реализуемой функции всегда чередуются. В заданной функции Z(p) можно также определить схему данного двухполюсника, его параметры, частоты резонансов напряжений и токов, начертить график зависимости Z(p) от частоты. Функция Z(p) реализуема, если она положительна и действительна, все коэффициенты при операторе  - только вещественные и положительные числа; высшая степень оператора
- только вещественные и положительные числа; высшая степень оператора  равна числу реактивных элементов в схеме. Разница между высшими и низшими степенями оператора
равна числу реактивных элементов в схеме. Разница между высшими и низшими степенями оператора  у числителя и знаменателя равны единице.
у числителя и знаменателя равны единице.
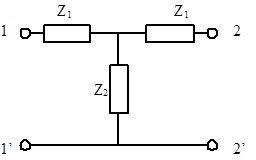
Рисунок 1 - Схема замещения исследуемого ЧП
Определим элементы, образующие данный четырехполюсник.
Формулы операторных сопротивлений согласно заданию имеют следующий вид:
 (1)
(1)
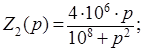 (2)
(2)
Исходя из формул (1) и (2), количество элементов в исследуемых двухполюсниках равно двум (максимальной степени комплексной переменной  ). Класс схемы определяется по значению сопротивлений на нулевой частоте и частоте, равной бесконечности:
). Класс схемы определяется по значению сопротивлений на нулевой частоте и частоте, равной бесконечности:

 ,
,
так как степень знаменателя больше степени числителя;
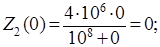
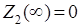 ,
,
так как степень знаменателя больше степени числителя;
Итак, класс обеих схем 0 - 0, т.е. схемы пропускают и ток низкой частоты и ток высокой частоты, и состоят из двух элементов: каждая - это параллельное соединение катушки индуктивности и конденсатора.

Рисунок 2 - Схема первого двухполюсника
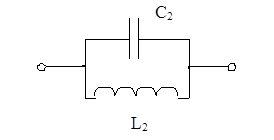
Рисунок 3 - Схема второго двухполюсника
Определим сопротивление первого двухполюсника, исходя из его схемы (рисунок 2):
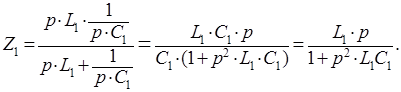
Сравнивая полученную формулу с заданной:

Можно сделать вывод, что  Гн,
Гн,  Ф.
Ф.
Сопротивление первого двухполюсника в канонической форме, исходя из соотношения 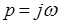 , где
, где  - мнимая единица:
- мнимая единица:
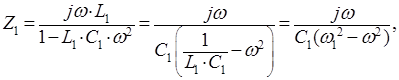
где  - резонансная частота (резонанс токов), равная
- резонансная частота (резонанс токов), равная 

Полюсно-нулевое изображение первого сопротивления и его характеристическая строка представлены на рисунке (4) и (5):

Рисунок 4 - Характеристическая строка сопротивления первого двухполюсника

Рисунок 5 - Полюсно-нулевое изображение первого двухполюсника
Рассчитаем значение  на контрольной частоте
на контрольной частоте  :
:

Сопротивление второго двухполюсника определяется аналогично первому.
Определяем сопротивление второго двухполюсника согласно схеме, изображенной на рисунке (3):
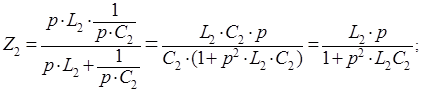
Сравнивая полученную формулу с заданной:

Можно сделать вывод, что 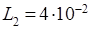 Гн,
Гн,  Ф.
Ф.
Сопротивление второго двухполюсника в канонической форме, исходя из соотношения  , где
, где  - мнимая единица:
- мнимая единица:

где 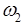 - резонансная частота (резонанс токов), равная
- резонансная частота (резонанс токов), равная 

Полюсно-нулевое изображение второго сопротивления и его характеристическая строка представлены на рисунке (6) и (7):

Рисунок 6 - Характеристическая строка сопротивления

Рисунок 7 - Полюсно-нулевое изображение второго двухполюсника
Рассчитаем значение  на контрольной частоте
на контрольной частоте 
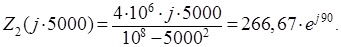
Частотные зависимости сопротивлений двухполюсников сведены в таблице (1). График частотных зависимостей сопротивлений двухполюсников представлен на рисунке (8).
Таблица 1 - Частотная зависимость сопротивлений двухполюсников, входящих в состав исследуемого четырехполюсника
| ω, рад/с | f, Гц |  , Ом , Ом  , Ом , Ом
| |
| 159,155 |  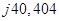
| ||
| 318,31 | 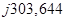 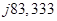
| ||
| 636,62 |  
| ||
| 795,775 | 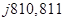 
| ||
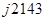 j j 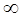
| |||
 
| |||
 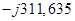
| |||
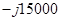 
| |||
   0 0
|