Вопросы к экзамену по дисциплине «Математика» за 1 семестр
Для студентов 1 курса ФЭА
Линейная алгебра
Определители, свойства, вычисление.
Матрицы. Виды матриц. Действия над матрицами. Вычисление обратной матрицы. Ранг и его вычисление.
Решение систем линейных уравнений.
С.л.а.у. с квадратичными матрицами и методы их решения (метод
Крамера, Гаусса, матричный способ)
Векторная алгебра
Векторы. Линейные операции над векторами.
Проекции вектора на ось.
Скалярное произведение векторов. Свойства. Применение.
Векторное произведение векторов. Свойства. Применение.
Смешанное произведение векторов. Свойства. Применение.
Векторный базис. Координаты вектора. Разложение вектора по базису.
11.Условия коллинеарности, ортогональности, компланарности векторов.
Аналитическая геометрия на плоскости и в пространстве.
Полярная система координат.
Прямая на плоскости.
Расстояние от точки до прямой. Угол между прямыми. Условия параллельности и перпендикулярности прямых.
Кривые второго порядка (окружность, парабола, эллипс, гипербола).
Плоскость. Частные случаи расположения плоскости.
Взаимное расположение плоскостей.
Нормальное уравнение плоскости. Расстояние от точки до плоскости. Уравнение плоскости, проходящей через три точки.
Прямая в пространстве. Угол между прямыми. Условия параллельности и перпендикулярности прямых. Угол между прямыми.
Условие принадлежности двух прямых одной плоскости. Взаимное расположение прямой и плоскости.
Поверхности второго порядка.
Математический анализ.
Дифференцирование функции одной переменной.
Множества. Числовые множества и промежутки.
Функция. Способы задания. Основные элементарные функции.
Предел функции в точке. Односторонние пределы.
Бесконечно малые и бесконечно большие функции. Свойства. Основные
Теоремы о пределах.
Первый и второй замечательные пределы.
Раскрытие неопределённостей.
Непрерывность функции. Точки разрыва. Свойства непрерывных функций.
Производная функции. Теорема о непрерывности дифференцируемой функции.
Правила дифференцирования.
Формулы дифференцирования. Производная сложной функции.
Производные неявной, степенной и показательной функций.
Логарифмическая производная, производная показательно-степенной функции.
Производная обратной функции. Производная обратных тригонометрических функций.
Дифференциал функции. Свойства. Геометрический смысл.
Теоремы Роля, Лагранжа, Коши.
Теорема Лопиталя.
Необходимое и достаточное условие возрастания (убывания) функции.
Экстремум функции в точке.
Наибольшее и наименьшее значения функции на отрезке.
Выпуклость, вогнутость графика функции. Точки перегиба.
Асимптоты кривой.
Общая схема исследования функции.
Функции многих переменных.
Определение функции нескольких переменных. Линии уровня. Поверхности Уровня. Непрерывность.
Частные и полные приращения функции.
Частные производные. Частный и полный дифференциал.
Производная сложной функции.
Производная от функции, заданной неявно.
Касательная плоскость, нормаль к поверхности.
Частные производные и дифференциалы высших порядков.
Экстремум. Необходимые и достаточные условия экстремума.
Примерные задания к экзамену по высшей математике (II семестр ОЗФ).
I. Функции нескольких переменных.
1. Найти частные производные функции
а) 
б) 
2. Найти 
, если 
3. Найти 
, 
, если 
4. Найти производную неявных функций, заданных уравнениями
а)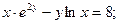 
б) 
5. Найти дифференциал функции 
?
6. Для функции, определенной неявно уравнением
а) 
найти 
б) 
найти 
.
7. Найти производную функции 
в точке 
по направлению к точке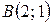 
.
8. Найти градиент функции 
и ее производную в точке 
в направлении 
.
9. Найти стационарные точки и исследовать на экстремум данные функции.
а) 
. б)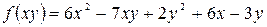 
.
10. Составить уравнение касательной плоскости и нормали к поверхности 
в точке 
.