Заместителем директора по УР
__________/______________/
(Подпись) (ФИО)
«____»________200___г.
Указания по проведению
практической работы № ___1____
Задачи на вычисление пределов
(Название работы)
По дисциплине «Математика»
Специальность __080110, 080112, 080501__
Разработал преподаватель
_____________(___................. __)
(Подпись) (ФИО)
«_______» _________________200___г.
Цель работы:
1. Формировать умения и навыки вычисления пределов
2. Формировать умения и навыки самостоятельного умственного труда
3. Прививать умения и навыки работы со справочным материалом
4. Определить уровень остаточных знаний студентов по данной теме
Перечень справочной литературы:
1. Богомолов Н.В. «Практические занятия по математике», М: Высшая школа, 2004
2. Письменный Д. «Конспект лекций по высшей математике», ч.1., Москва, Айрис-Пресс, 2004
3. Шипачев В.С. «Задачник по высшей математике», М: Высшая школа, 2003
4. Выгодский М.Я. «Справочник по высшей математике», Росткнига, 2001
Краткие теоретические сведения:
Предел последовательности
Определение. Число 
называется пределом последовательности 
, если для любого положительно 
го числа найдется такое натуральное число 
, что при всех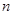 
> 
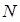выполняетсянеравенство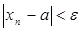 
Пишут: 
Графически это выглядит так:
n - 
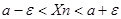
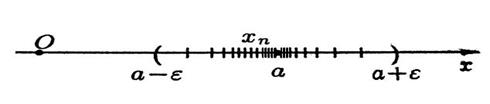
Т.е. элемент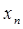 
находится в 
- окрестности точки а. При этом последовательности 
называется сходящейся, в противном случае – расходящейся.
Основные свойства сходящихся последовательностей
1)Сходящаяся последовательность ограничена.
2)Пусть 
, 
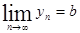, тогда а) 
б) 
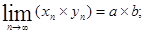в) 
3)Если 
и для всех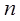 
выполняется неравенства 
, то 
. 
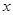
4) Если 
и последовательность {уn}- ограниченная, то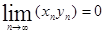 
| №1. Найти пределы: | |
| 
|
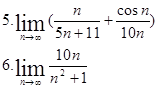
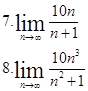
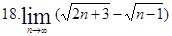
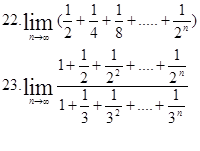
Бесконечно большие и бесконечно малые функции
Определение. Функция 
называется бесконечно малой при 
, если 
Например: 1)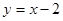 
при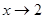 
б. м. ф. т.к. 
2) 
при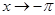 
б. м. ф. т. к 
Определение. Функция 
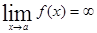называется бесконечно большой при , если 
, 
или 
Например, 
есть б. б. Ф при 
; 
если б. б. ф. при 
действительно 
и 
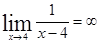
Теорема (о связи между функций, ее приделом и бесконечно малой функцией). Если функция 
имеет придел, равный 
, то ее можно представить как сумму числа и бесконечно малой функции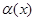 
, т.е. если 
Теорема (обратная). Если функцию можно представить в виде суммы числа А и б.м.ф.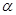 
(x), то число А является пределом функции 
, т.е если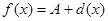 
, то 
Например, требуется вычислить 
. Представим числитель и знаменатель в виде суммы числа и б.м.ф. 
Функции 
при 
есть б.м.ф. таким образом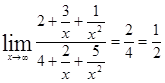 
Основные теоремы о пределах
Теорема 1. Предел суммы (разности) двух функций равен сумме (разности) их пределов:
Теорема справедлива для алгебраической суммы любого конечного числа функций.
Теорема 2. Функция может иметь только один предел при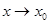 
.
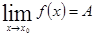
Теорема 3. Предел произведения двух функций равен произведению их пределов:
.
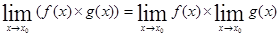Следствие 1. Постоянный множитель можно выносить за знак предела: 
Следствие 2. Предел степени с натуральным показателем равен той же степени предела: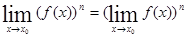 
.
Теорема 4. Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя не равен нулю.
Примеры:
1) 
= 
= 
= 
=
= 
= 
= 
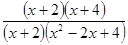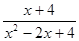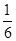
2) 
=
= 
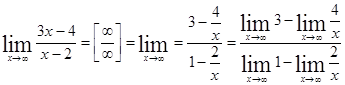3) 
Первый замечательный предел
Второй замечательный предел
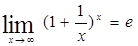или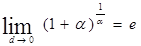 
Примеры:
Вычислить:
1) 
.
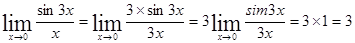2) 
.
3) 
4) 
= 
= 
= 
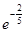
№2. Найти пределы: 
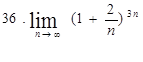
№3. Найти пределы:
  
|    
|
| 
|
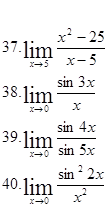
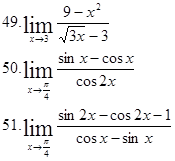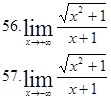
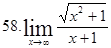
Порядок проведения работы:
1. Используя теоретические сведения выполнить предложенное преподавателем задание
2. Соответствующим образом оформить работу
| Лист 1. Практическая работа по теме «Вычисление пределов» Выполнил:__________ (ФИО) группа:_____________ Проверил:__________ Оценка:____________ | Лист 2. № примера Решение: Ответ: |
Оформление работы: