1.Релейшая схема (рис.7) состоит из 6 элементов. Пусть события А1 (і= 
) состоят в том, что соответствующие элементы работают безотказно в течение времени Т. Выразить через А1 событие, состоящее в том, что схема за время Т работает безотказно.
Ответ:
2. Набирая номер телефона, абонент забыл 2 последние цифры и набрал их наугад. Найти вероятность того, что набраны нужные цифры.
Ответ:
3. Сколько трехзначных чисел можно составить из цифр 1,2,3,4,5, если: а) цифры не повторяются? б) цифры могут повторяться?
Ответ:
4. В студенческой группе 14 девушек и 6 юношей. Сколькими способами можно выбрать, для выполнения различных заданий, двух студентов одного пола?
Ответ:
5. Сколькими способами можно выбрать 3 цветка из вазы, в которой стоят 10 красных и 4 розовых гвоздики? А если выбрать 1 красную гвоздику и 2 розовых?
Ответ:
6. Сколько пятизначных чисел можно составить, используя цифры: а)2,5,7,8; б)0,1,9?
Ответ:
7. Сколькими способами можно составить букет из 5 цветов, если в наличии есть цветы трех сортов?
Ответ:
8.Сколько различных пятизначных чисел можно составить из цифр 3,3,5,5,8?
Ответ:
9. Из 4 первокурсников, 5 второкурсников и 6 третьекурсников надо выбрать 3 студента на конференцию. Сколькими способами можно осуществить этот выбор, если среди выбранных должны быть студенты разных курсов.
Ответ:
10. Сколькими способами можно распределить 15 выпускников по трем районам, если в одном из них имеется 8, в другом- 5 и в третьем- 2 вакантных места?
Ответ:
11. В почтовом отделении имеются открытки 6 видов. Какова вероятность того, что среди 4 проданных открыток все открытки: а) одинаковы, б) различны?
Ответ:
12. В барабане револьвера 7 гнезд, из них в 5 заложены патроны. Барабан приводится во вращение, потом нажимается спусковой курок. Какова вероятность того, что повторив такой опыт 2 раза подряд: а) оба раза не выстрелит; б) оба раза револьвер выстрелит?
Ответ:
13. Из букв разрезной азбуки составлено слово СТАТИСТИКА. Какова вероятность того, что, перемешав буквы и укладывая их в ряд по одной (наудачу), получим слово: а) ТИСКИ; б)КИСКА; в) КИТ; г) СТАТИСТИКА?
Ответ:
14. Надежность (т.е. вероятность безотказной работы) прибора равна 07. Для повышения надежности данного прибора он публикуется n-1 другими такими же приборами (рис.13) Сколько приборов надо взять, чтобы повысить его надежность до 0,95?
Ответ:
15. Прибор содержит две микросхемы. Вероятность выхода из строя в течение 10 лет первой микросхемы равна 0,07, а второй – 0,10. Известно, что из строя вышла одна микросхема. Какова вероятность того, что вышла из строя первая микросхема?
Ответ:
16. Из 40 экзаменационных билетов студент П выучил только 30. Каким выгоднее ему зайти на экзамен, первым или вторым?
Ответ:
17. В семье трое детей. Какова вероятность того, что: а) все они мальчики; б) один мальчик и две девочки. Считать вероятность рождения мальчика 0,51, а девочки – 0,49.
Ответ:
18. В каждом из карманов (их «) лежит по коробку спичек (по 10 спичек в коробке). При каждом закуривании карман выбирается наудачу. При очередном закуривании коробок оказался пустым. Найти вероятность того, что во втором коробке 6 спичек.
Ответ:
19. Найти вероятность того, что при бросании 3-х игральных костей шестерка выпадет на одной кости, если на гранях 2-х других костей выпадут числа очков, не совпадет между собой (и не равные 6)
Ответ:C
n= 
m= 
P= 
20. На складе имеется 15 кинескопов, причем 10 из них изготовлены Львовским заводом. Найти Р того, что среди 5 взятых наудачу кинескопов окажутся 3 кинескопа Львовского завода.
21. В «секрете» замке на общей оси 4 диска, каждый из которых разделен на 5 секторов, на которых написаны различные цифры. Замок открывается только в случае, если диски установлены так, что цифры на них составляют определенное четырехзначное число. Найти Р того, что при произвольной установке дисков замок будет открыт.
22. Быстро вращающийся диск разделен на четное число равных секторов, попеременно окрашенных в белый и черный цвет. По диску произведен выстрел. Найти Р того, что пуля попадет в один из белых секторов.
23. В читальном зале имеется 6 учебников по ТВ, из которых 3 в переплете. Библиотекарь наудачу для 2 учебника. Найти Р того, что оба учебника окажутся в переплете.
Ответ:
P(AB)= P(A)* P(B/A)= 
= 
=0,2
24. В цехе работают 7 мужчин и 3 женщины. По табличным нормам наудачу отобраны 3 человека. Найти Р того, что все отобранные лица окажутся мужчинами.
Ответ:
А- первым отобран мужчина
В- вторым отобран мужчина
С- третьим отобран мужчина
Р(АВС)= Р(А)* Р(В/А)Р(С/АВ)= 
* 
* 
= 
25. По данным переписи населения (1891 г.) Англии и Уэльса установлено: темноглазые отцы и темноглазые сыновья (АВ) составляют 5% обследованных лиц, темноглазые отцы и светлоглазые сыновья (
) – 7,9%, светлоглазые отцы и темноглазые сыновья (
) – 8,9%, светлоглазые отцы и светлоглазые сыновья (
)- 78,2 %. Найти связь между цветом глаз отца и сына.
Ответ:
По условию Р(АВ)=0,05
Р(
)=0,079
Р(
В)=0,089
Р(
)=0,782
Найдем условные вероятности того, что сын темноглазый, если отец темноглазый
Р(А/В)= 
= 
= 
=0,39
Сын светлоглазый, если отец темноглазый
Р(
/А)=1-Р(В/А)=1-0,39=0,61
Сын темноглазый, если отец светлоглазый
Р(В/ )= 
= 
= 
=0,102
Сын светлоглазый, если отец светлоглазый
Р( / )= 1-0,102=0,898
26. Для разрушения моста достаточно попадания одной авиационной бомбы. Найти Р того, что мост будет разрушен, если на него сбросить 4 бомбы, вероятности попадания которых соответственно равны 0,3; 0,4; 0,6; 0,7.
27. Число грузовых автомашин, проезжающих по шоссе, на котором стоит бензоколонка относиться к числу легковых машин, проезжающих по тому же шоссе как 3:2 Р того, что будет заправляться грузовая машина, равна 0,1; для легковой эта Р=0,2; к бензоколонке подъехала для заправки машина. Найти Р того, что это грузовая машина.
28. Батарея из трех орудий произвела, причем 2 снаряда попали в цель. Найти Р того, что первое орудие дало попадание, если вероятность попадания в цель первым, вторым и третьим орудием, соответственно р1=0,4; р2=0,3; р3=0,5.
Ответ:
А- 2 орудие попало в цель
Н1- первое орудие попало в цель
Н2- первое орудие не попало в цель
Р(Н2)= 0,6
Р(А/Н1)=0,3*0,5+0,5*0,7= 0,5
Р(А/Н2)= 0,3*0,5=0,15
Р(Н1/А)= 
= 
29. Товаровед осматривает 24 образца товаров. Р того, что каждый из образцов будет признан годным к продаже 0,6. Найти число образцов, которые товаровед признает годными к продаже.
Ответ:
n= 24 p=0.6 g=0.4
24*0,6-0,4 
k0 
24*0,6+0,6
14 k0 15
Ответ:14; 15
30. Среднее число заказов такси, поступающих на диспетчерский пункт в одну минуту, равно трем. Найти Р того, что за 2 минуты поступает:
а) четыре вызова;
б) менее четырех вызовов;
в) не менее четырех вызовов.
Ответы:
λ=3 t=2 k=4 По формуле Пуассона
Pt(k)= 
а) P2(4)= 
= 
=0,135
б) P2(k<4)= P2(3)+ P2(2)+P2(1)+ P2(0)= 
(36+18+6+1)= 0.0025*61=0.1525
в) P(k≥4)=1-0.1525=0.8475
31. Завод “Золотая балка” (Крым) оптравил в Москву 1500 бутылок вина “Каберне”. Вероятность токо, что в пути бутылка может разбиться, равна 0002. Найти вероятность токо, что в пути будет разбито не более 4-х бутылок (события А).
Ответ:
32. Телефонна станция обслуживает 2000 абонентов. Вероятность позвонить любому абоненту в течение часа равна 0,003. Какова вероятность того, что в течение часа позвонят 5 абонентов?
33. Вероятность попадения в цель при одном выстреле равна 0,6. Анйти вероятность токо, что при n =1200 независимых выстрелах отклонение «частости» от вероятности по модулю не превышает 
=0,05.
34. На лекции по теории вероятностей присуствуют 84 студента. Какова вероятность токо, что среди них есть 2 студента, у которых сегодня день рождения?
35. В урне 8 шаров, из которых 5 белых, а остальные – черные. Из нее вынимают наудачу 3 шара. Найти закон распределения числа белых шаров в выборке.
36. Два стрелка делают по одному выстрелу в одну мишень. Вероятность попадания для первого стрелка равна 0,6, а для второго 0,8. Найти и построить функцию распределения с.в. Х- числа попаданий в мишень.
Ответ:
37. Является ли плотность распределения некоторой с.в. каждая из следующих ыункций:
Ответ:
38. В лотерее имеется 1000 билетов, из них выигрышных: 10 по 500 руб, 50 по 50 руб, 150 по 1 руб. Найти математическое ожидание выигрыша на один билет.
39. Д. с. в. Х задана рядом распределения
Найти МХ, DX, 
х
41. Производится 3 независимых выстрела по цели. Вероятность попадания при разных выстрелах одинаковы и равны р=0,9. Найти м.о. числа попаданий. Решить задачу в случае, если вероятность попадания при разных выстрелах различны: а)р1=0,7, б)р2=0,8, в)р3=0,9.
42. Пусть X и Y – независимые д. с. В., причем МХ=2, М Y= -3, DX=2, DY=9. Найти MZ и DZ, если Z= 5Х-3Y+2.
Ответ:
43. Вероятность попадения в цель при отдельном выстреле для данного стрелка равна 0,1. Найти математическое ожидание и дисперсию с. в. Х- числа выстрелов по цели до первого попадания.
Ответ:
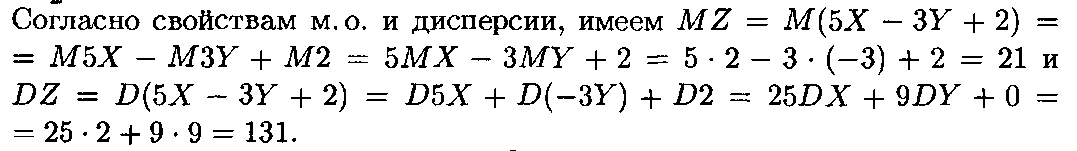
44. Случайная величина Т- время рабиолампы имеет показательное распределение. Найти вероятность того, что лампа проработает не менее 800 часов, если среднее время работы радиолампы 400 часов.
45. В урне 4 шара: 2 белых, 1 черный, 1 синий. Из нее наудачу извлекают два шара. Пусть с. в. Х- число черных шаров в выборке, с. в. Y- число синих шаров в выборке. Составить закон распределения для системы (Х, Y). Найти законы распределения Х и Y.
46. В урне 4 шара: 2 белых, 1 черный, 1 синий. Из нее наудачу извлекают два шара. Пусть с.в. Х- число черных шаров в выборке, с.в. Y- число синих шаров в выборке. Составить закон распределения для системы (X,Y). Найти законы распределения X и Y.
Ответ:
