Модуль 1. Функция одной переменной, ее свойства.
Найти область определения функции:
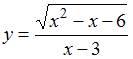

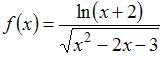


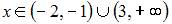

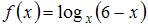






Область определения функции  имеет вид
имеет вид 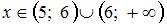 . Тогда значение
. Тогда значение  равно …5
равно …5
Модуль 2. Предел функции одной переменной.
Вычислить пределы функций
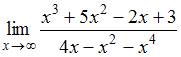 (0)
(0)  (
( )
)
 (-2)
(-2)  (
( )
)
 (
( )
)  (0)
(0)
 (3)
(3) 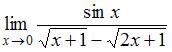 (-2)
(-2)
 (
(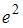 )
)  (1)
(1)
Модуль 3. Непрерывность функции одной переменной.
Исследовать на непрерывность следующие функции (указать точки разрыва и определить какого они рода)







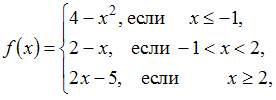

Модуль 4. Дифференцируемость функции одной переменной.
Найти производную функции  :
:
 (
( )
)
 (
(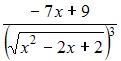 )
)
 (
(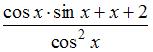 )
)
 (
( )
)
 (
( )
)
Найти производную функции, заданной параметрически:
 (
(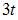 )
)  (
( )
)
Модуль 5. Применение производной к исследованию функций.
Материальная точка движется прямолинейно по закону 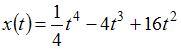 . Тогда скорость точки в момент времени
. Тогда скорость точки в момент времени  равна …(24)
равна …(24)
Материальная точка движется прямолинейно по закону  . Тогда ускорение точки в момент времени
. Тогда ускорение точки в момент времени  равно …(0)
равно …(0)
К графику функции  в его точке с абсциссой
в его точке с абсциссой  проведена касательная. Тогда площадь треугольника, образованного касательной и отрезками, отсекаемыми ею на осях координат, равна …(4)
проведена касательная. Тогда площадь треугольника, образованного касательной и отрезками, отсекаемыми ею на осях координат, равна …(4)
Уравнение касательной к графику функции  в его точке с абсциссой
в его точке с абсциссой  имеет вид …(
имеет вид …( )
)
Максимум функции  равен …(
равен …( )
)
Минимум функции  равен …(
равен …(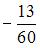 )
)
Наибольшее значение функции  на отрезке
на отрезке  равно …(-1)
равно …(-1)
Наименьшее значение функции 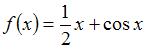 на отрезке
на отрезке 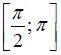 равно …(
равно …( )
)
Промежуток возрастания функции  имеет вид …
имеет вид … 
Исследовать на выпуклость вогнутость, найти точки перегиба функции
а)  б)
б) 
Найти уравнения горизонтальных асимптот для функций:
 (
( )
) 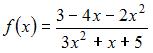 (
( )
)
Найти уравнения вертикальных асимптот для функций:
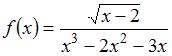 (
( )
)  (
( )
)
 (х = 1)
(х = 1)  (
( )
)
Найти уравнения наклонных асимптот для функций:
 (
( )
)  (
( )
)
Вычислить предел функции, используя правило Лопиталя: 
Модуль 6. Функция нескольких переменных.
Частная производная 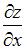 функции
функции  имеет вид …
имеет вид … 
Частная производная 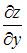 функции
функции  имеет вид …
имеет вид … 
Частная производная  функции
функции 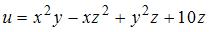 имеет вид
имеет вид  …
…
Значение частной производной 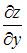 функции
функции  в точке
в точке  равно
равно  …
…
Частная производная второго порядка  функции
функции  имеет вид …
имеет вид … 
Частная производная второго порядка  функции
функции  имеет вид …
имеет вид … 
Приближенное значение функции  в точке
в точке  , вычисленное с помощью полного дифференциала, равно …
, вычисленное с помощью полного дифференциала, равно … 
Приближенное значение функции  в точке
в точке  , вычисленное с помощью полного дифференциала, равно …5,002
, вычисленное с помощью полного дифференциала, равно …5,002
Градиент скалярного поля  в точке
в точке 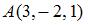 равен …
равен … 
Модуль градиента скалярного поля  в точке
в точке  равен …
равен … 
Модуль градиента скалярного поля  в точке
в точке  равен …3
равен …3
Градиент скалярного поля  равен нулевому вектору в точке …
равен нулевому вектору в точке … 
Смешанная частная производная второго порядка 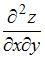 функции
функции  имеет вид …
имеет вид … 
Полный дифференциал функции  имеет вид …
имеет вид … 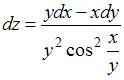
Неявная функция  определяется как решение уравнения
определяется как решение уравнения  . Тогда производная первого порядка
. Тогда производная первого порядка  при
при  равна …0
равна …0
Функция  задана в неявном виде
задана в неявном виде 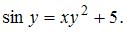 Тогда производная первого порядка функции
Тогда производная первого порядка функции  по переменной
по переменной 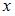 имеет вид …
имеет вид … 
Модуль 7.Неопределенный интеграл.
Найти первообразные функций:
 (
( )
)  (
( )
)
 (
( )
)  (
( )
)
 (
(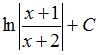 )
)  (
( )
)
 (
(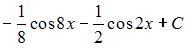 )
) 
( )
) 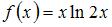 (
( )
)
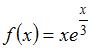 (
( )
)
Модуль 8. Определённый интеграл.
Найти среднее значение функции 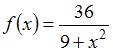 на отрезке
на отрезке  (
( )
)
Найти среднее значение функции 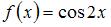 на отрезке
на отрезке  (
(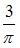 )
)
Вычислить определенный интеграл:
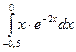
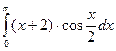
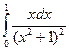



 и т. д.
и т. д.
Вычислить несобственный интеграл или установить его расходимость:
1)  2)
2) 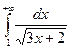 3)
3)  4)
4) 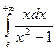 5)
5)  и т. д.
и т. д.
Вычислить площадь фигуры, ограниченной графиками функций, а также объем тела, полученного вращением вокруг указанной оси фигуры, ограниченной графиками функций:
1. y = x2, y = 2 – x, y = 0,  ,
, 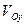
2. y =  y = 7 – x,
y = 7 – x,  ,
, 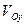
3. y = lnx, x = e, y = 0, 
4. y =  x + y = 2, y = 0,
x + y = 2, y = 0,  ,
, 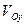
5. y = x2 + 4x, y = x + 4.
6. y = x2 – 4x + 4, y = x, 
7.  y = x, x = 4,
y = x, x = 4,  ,
, 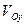 и т. д.
и т. д.
Вычислить площадь фигуры, изображенной на рисунке


( ) (6)
) (6)


( ) (
) ( )
)
 (
( )
)
Найти площадь фигуры, ограниченной параболой  и осью
и осью  .(36)
.(36)
Найти объем тела, полученного вращением вокруг оси 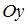 криволинейной трапеции, ограниченной параболой
криволинейной трапеции, ограниченной параболой  и осью
и осью 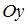 .(
.( )
)