Введение
При осуществлении проектов в машиностроительной области, начальной стадией реализации этого проекта является создание модели, которая по возможности могла бы учитывать все факторы, влияющие на качество, надежность, долговечность, заданные характеристики работы при эксплуатации. В соответствии с условиями работы и заданными техническими характеристиками необходимо спроектировать такую модель, которая бы отвечала всем поставленным требованиям. Однако в процессе разработки приходится воплощать несколько моделей и сравнивать их характеристики между собой для более оптимального решения проблемы, в этих случаях наиболее целесообразно использовать ЭВМ.
Автоматизация машиностроения требует не только автоматического управления режимами, например, механической обработки, прессования, термической, физико-химической обработки и других рабочих процессов машиностроения. Для полной механизации работ требуется автоматизация транспортирования (перемещения в пространстве) и переориентация объекта производства. В качестве такого объекта манипулирования может быть обрабатываемая деталь, инструмент или другой предмет самой разнообразной конфигурации. Чаще всего требуется не только переместить в пространстве, но и сориентировать деталь определенным образом, т.е. не только изменить ее местонахождение, но и развернуть в пространстве определенным образом. Эти операции выполняются манипуляторами промышленных роботов.
Постановка задачи
Деревянная балка полетом  защемлен левым концом. На правом свободном конце приложена сила
защемлен левым концом. На правом свободном конце приложена сила 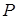 . Диаметр одной балки
. Диаметр одной балки  , другой -
, другой - 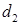 (рис. 1).
(рис. 1).
Исследовать прогибы балки  при различных значениях силы
при различных значениях силы 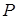 (весом балки пренебречь). Построить графики зависимостей
(весом балки пренебречь). Построить графики зависимостей  в одних осях координат.
в одних осях координат.

Исходные данные:
Длина пролета балки l=400 мм
Момент инерции одной части балки J1=10000 кг*мм²
Момент инерции одной части балки J2=28600 кг*мм²
Модуль упругости E=49000 MПa
Сила P1=50 H
Сила P2=200 H
Сила P3=1000 H
Количество разбиений n=10
Математическая модель решения задачи
Для определения прогиба используем теорему Кастильяно.
Частная производная от потенциальной энергии деформации по обобщенной силе равна соответствующей обобщенной координате.
Для консольной балки, на свободный конец которой действует сосредоточенная сила, прогиб  является обобщенно координатой, соответствующей этой силе.
является обобщенно координатой, соответствующей этой силе.

где  -модуль упругости;
-модуль упругости;
 - момент инерции площади поперечного сечения балки
- момент инерции площади поперечного сечения балки
Т.к. 
Выражение для величины искомого прогиба балки переменного сечения имеет следующий вид:
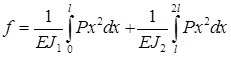
где 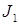 - момент инерции первого сечения,
- момент инерции первого сечения,
 - момент инерции второго сечения.
- момент инерции второго сечения.
Вычисление интеграла методом трапеций.
Интеграл оценивается вычислением суммы площадей элементарных трапеций со сторонами, равными значениям f(x) в начале и конце элементарного отрезка. Это приближение равносильно замене функции отрезком прямой, соединяющей значения f(x) в начальной и конечной точках отрезка (рис. 2).

Рис. 2. Метод трапеции
Площадь каждого элементарного сегмента разбиения считается по формуле

где h=(b-a)/n.
Тогда площадь искомой фигуры будем искать по формуле:

Следовательно, формула трапеций для численного интегрирования имеет вид:

Алгоритм решения задачи
. Вводим исходные данные
l, J1, J2, E, P1, P2, P3, n
. k:=1; r:=2; T:=0;
Вычисляем прогиб под действием силы P1 c помощью процедуры Integral
3. Integral (0, l, P1, E, J1, T, n, k, r, A, f);
. k:=n+1; r:=n+2; T:=f [n+1];
. Integral (l, 2*l, P1, E, J2, T, n, k, r, A, f);
6. Записываем в фаил REZ.REZ посчитанные значение прогиба в зависимости от длины балки с помощью процедуры Vivod
6.1 vivod (A, n);
vivod (f, n);
7. k:=1; r:=2; T:=0;
Вычисляем прогиб под действием силы P1 c помощью процедуры Integral
8. Integral (0, l, P2, E, J1, T, n, k, r, A, f);
. k:=n+1; r:=n+2; T:=f [n+1];
. Integral (l, 2*l, P2, E, J2, T, n, k, r, A, f);
11. Записываем в фаил REZ.REZ посчитанные значение прогиба в зависимости от длины балки с помощью процедуры Vivod
12.1 vivod (A, n);
vivod (f, n);
13. k:=1; r:=2; T:=0;
Вычисляем прогиб под действием силы P1 c помощью процедуры Integral
14. Integral (0, l, P3, E, J1, T, n, k, r, A, f);
. k:=n+1; r:=n+2; T:=f [n+1];
. Integral (l, 2*l, P3, E, J2, T, n, k, r, A, f);
17. Записываем в фаил REZ.REZ посчитанные значение прогиба в зависимости от длины балки с помощью процедур Vivod
18.1 vivod (A, n);
vivod (f, n);
Процедура Vivod
. Для i=1…2*n+1
1.1 write (a[i])
Алгоритм процедуры INTEGRAL
. h:=(konec-nach)/n
. Для i=1…n+1
x[i]:=nach+(i-1)*h;
q[i]:=x[i]*x[i];
A[k]:=x[i];
k:=k+1;
. temp:=0 f[1]:=0
. Для i=2…n+1
temp:=temp+(q[i]+q [i-1])/2*h;
f[r]:=T+(P*temp)/(E*J);
4.3 r:=r+1;
Схема алгоритма
Процедура Vivod

Процедура INTEGRAL

Схема головной программы
Таблица идентификаторов
| Наименование | физический смысл | идентификатор |
| Сила действующая на балку | P1 | P1 |
| Сила действующая на балку | P2 | P2 |
| Сила действующая на балку | P3 | P3 |
| Длина пролета балки | l | l |
| Момент инерции одной части балки | J1 | J1 |
| Момент инерции второй части балки | J2 | J2 |
| Прогиб балки | f | f |
| Счетчики | - | k, r |
| Координата | x | A |
 T T
|
прогиб балка программа сечение
Текст программы
program kursach;crt;vect=array [1..30] of real;T, l, J1, J2, P1, P2, P3, E:real;, n, k:integer;, f:vect;:text;vivod (a:vect; n:integer);i:integer;i:=1 to 2*n+1 do(s, a[i]:6:2,' ');;INTEGRAL (nach, konec, P, E, J, T:real; n, k, r:integer; Var A, f:vect);i:byte;:real;, x:vect;:real;:=(konec-nach)/n;i:=1 to n+1 do[i]:=nach+(i-1)*h;[i]:=x[i]*x[i];[k]:=x[i];:=k+1;;:=0; f[1]:=0;i:=2 to n+1 do:=temp+(q[i]+q [i-1])/2*h;[r]:=T+(P*temp)/(E*J);:=r+1;;;;(s, 'rez.rez');(s);(s);
write ('Введите длину пролета балки l=');
readln(l);('Введите момент инерции одной части балки J1=');(J1);('Введите момент инерции другой части балки J2=');(J2);('Введите модуль упругости E=');
readln(E);('Ведите силу P1=');(P1);
write ('Ведите силу P2=');
readln(P2);('Ведите силу P3=');(P3);
write ('Введите количество разбиений n=');(n);(s, ' ':25,'КУРСОВОЙ ПРОЕКТ');(s, ' ':8,'ТЕМА: Исcледование прогиба балки переменного сечения');
writeln(s);(s, ' ':26,'Группа 103114');
writeln (s, ' ':20,'Бражкин Виталий Иванович');
writeln (s, ' ':27,'Вариант 20');
writeln(s);(s, ' ':15,'Исходные данные:');(s, ' ':10,'Длина пролета балки l=', l:5:2,' ', 'мм');(s, ' ':10,'Момент инерции одной части балки J1=', J1:8:2,' ', 'кг*мм²');(s, ' ':10,'Момент инерции одной части балки J2=', J2:8:2,' ', 'кг*мм²');(s, ' ':10,'Модуль упругости E=', E:8:2,' ', 'MПa');
writeln (s, ' ':10,'Сила P1=', P1:5:2,' ', 'H');(s, ' ':10,'Сила P2=', P2:6:2,' ', 'H');(s, ' ':10,'Сила P3=', P3:7:2,' ', 'H');
writeln (s, ' ':10,'Количество разбиений n=', 2*n:2);
writeln(s);:=1; r:=2; T:=0;(0, l, P1, E, J1, T, n, k, r, A, f);:=n+1; r:=n+2;:=f [n+1];(l, 2*l, P1, E, J2, T, n, k, r, A, f);
writeln(s);(s, ' ':5,'Прогибы балки в разных точках под действием силы P=50H');
writeln(s);(s, 'x(мм)', ' ');(A, n);(s);(s);(s, 'f(мм)', ' ');(f, n);(s);(s);:=1; r:=2; T:=0;(0, l, P2, E, J1, T, n, k, r, A, f);:=n+1; r:=n+2;:=f [n+1];(l, 2*l, P2, E, J2, T, n, k, r, A, f);
writeln(s);(s, ' ':5,'Прогибы балки в разных точках под действием силы P=200H');
writeln(s);(s, 'x(мм)', ' ');(A, n);(s);(s);(s, 'f(мм)', ' ');(f, n);(s);(s);:=1; r:=2; T:=0;(0, l, P3, E, J1, T, n, k, r, A, f);:=n+1; r:=n+2;:=f [n+1];(l, 2*l, P3, E, J2, T, n, k, r, A, f);
writeln(s);(s, ' ':5,'Прогибы балки в разных точках под действием силы P=1000H');
writeln(s);(s, 'x(мм)', ' ');(A, n);(s);(s);(s, 'f(мм)', ' ');(f, n);(s);
writeln ('Результаты расчета записаны в фаил REZ.REZ');
close(s);until keypressed.