Традиционная методическая схема изучения тригонометрических функций:
· в начале определяются тригонометрические функции для острого угла прямоугольного треугольника;
· затем введенные понятия обобщаются для углов от  до
до 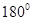 ;
;
· тригонометрические функции определяются для произвольных угловых величин и действительных чисел.
В курсе алгебры и начала анализа осуществляется заключительный этап изучения, который включает:
a) Закрепление представлений учащихся о радианной мере угла; отработка навыков перехода от градусной меры к радианной и наоборот;
b) Формирование представлений об углах с градусной мерой, большей  ; формирование представлений об углах с положительной и отрицательной градусными мерами; перевод этих градусных мер в радианы (положительные и отрицательные действительные числа);
; формирование представлений об углах с положительной и отрицательной градусными мерами; перевод этих градусных мер в радианы (положительные и отрицательные действительные числа);
c) Описание тригонометрических функций на языке радианной меры угла;
d) Утверждение функциональной точки зрения на  ,
,  , и
, и  (трактовка
(трактовка  ,
,  , и
, и  как функций действительного аргумента, установление области определения, области значений, построение графика функции, установление промежутков монотонности, знакопостоянства и т.д.);
как функций действительного аргумента, установление области определения, области значений, построение графика функции, установление промежутков монотонности, знакопостоянства и т.д.);
e) Повторение известных и ознакомление с новыми тригонометрическими тождествами, ключом которых является тождество  ;
;
f) Применение тригонометрических тождеств в тождественных преобразованиях и при решении задач по стереометрии.
В курсе "Алгебра 9" учащиеся знакомятся с функциональной точкой зрения. Выражения  и
и  определимы при
определимы при 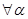 , т.к
, т.к  угла поворота можно найти соответствующее значение дробей
угла поворота можно найти соответствующее значение дробей 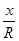 и
и  . Выражение
. Выражение  имеет смысл при
имеет смысл при  , кроме углов поворота
, кроме углов поворота 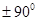 ,
,  , …, т.к. имеет смысл дробь
, …, т.к. имеет смысл дробь  .
.
Каждому допустимому значению  соответствует единственное значение
соответствует единственное значение  ,
,  ,
,  и
и  . Поэтому
. Поэтому  ,
,  ,
, 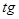 и
и 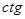 являются функциями угла
являются функциями угла 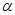 . Их называют тригонометрическими функциями.
. Их называют тригонометрическими функциями.
Учащиеся знакомятся со следующими общефункциональными свойствами этих функций:
1. область значения  и
и  -
- 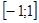 , для
, для 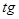 и
и 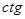 - множество всех действительных чисел
- множество всех действительных чисел
2. промежутки знакопостоянства:  , то значит
, то значит  зависит от знака
зависит от знака  и т.д.
и т.д.
3.  ,
, 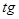 и
и 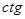 являются нечетными функциями, а
являются нечетными функциями, а  является четной функцией
является четной функцией
4. при изменении угла на целое число оборотов значение  ,
,  ,
, 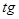 ,
,  не изменится (под обратным понимаем поворот на
не изменится (под обратным понимаем поворот на  ).
).
Введение радианной меры угла основывается на том факте, что отношения длины окружности к её радиусу постоянно для данного центрального угла и не зависит от выбора концентрических окружностей. По этой причине меру центрального угла можно охарактеризовать действительным числом 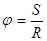 . Если
. Если 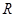 положить равным 1, то радианная мера центрального угла равна 1, т.е.
положить равным 1, то радианная мера центрального угла равна 1, т.е.  .
.
Тогда для каждого угла, заданного в градусах, достаточно вычислить соответствующую дугу единичной окружности. Длина такой дуги будет выражать меру данного угла в радианах.
Радианная мера угла позволяет любому действительному числу поставить в соответствие определенную градусную меру угла по формуле: 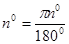 , где
, где 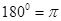 .
.
Переход от радианной меры угла к действительному числу осуществляется на основании того, что  . Учащимся следует показать изменение величин углов по координатным углам:
. Учащимся следует показать изменение величин углов по координатным углам:
1 четверть: 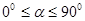 ,
,  ;
; 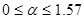
2 четверть:  ,
,  ;
;  и т.д.
и т.д.
Определение тригонометрической функции  выглядит так:
выглядит так:
Опр. Окружность радиуса 1 с центром в начале координат называют единичной
окружностью. Пусть точка  единичной окружности получена при повороте точки
единичной окружности получена при повороте точки 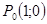 на угол в
на угол в  радиан. Ордината точки
радиан. Ордината точки  - это синус угла
- это синус угла 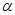 . Числовая
. Числовая  функция, заданная формулой
функция, заданная формулой  , называется синусом числа, каждому числу
, называется синусом числа, каждому числу  ставится в соответствие число
ставится в соответствие число  .
.
Устанавливаются области определения и значения функций, напоминаются свойства:
 ;
;  .
.
Построим график функции  на
на  .
.
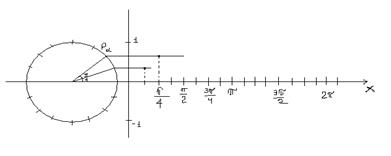
Делим единичную окружность и отрезок  на 16 равных частей.
на 16 равных частей.
Через точку  проводим прямую, параллельную
проводим прямую, параллельную  . Проводим прямую
. Проводим прямую  до пересечения с построенной прямой. Получим одну из точек графика функции
до пересечения с построенной прямой. Получим одну из точек графика функции  , называемого синусоидой.
, называемого синусоидой.
Отрезок оси 
 , с помощью которого находятся значения синуса, называется линией синусов.
, с помощью которого находятся значения синуса, называется линией синусов.
Для построения графика синуса вне этого отрезка заметим, что  . Поэтому во всех точках вида
. Поэтому во всех точках вида  , где
, где  , значения синуса совпадают, и, следовательно, график синуса на всей прямой получается из построенного графика с помощью параллельных переносов его вдоль оси
, значения синуса совпадают, и, следовательно, график синуса на всей прямой получается из построенного графика с помощью параллельных переносов его вдоль оси  .
.
Для построения графика косинуса следует вспомнить, что  . Следовательно, значение косинуса в произвольной точке
. Следовательно, значение косинуса в произвольной точке  равно значению синуса в точке
равно значению синуса в точке  . Это значит, что график косинуса получается из графика синуса с помощью параллельного переноса на расстояние
. Это значит, что график косинуса получается из графика синуса с помощью параллельного переноса на расстояние  в отрицательном направлении оси
в отрицательном направлении оси  . Поэтому график функции
. Поэтому график функции  также является синусоидой.
также является синусоидой.
Для функций  и
и 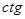 определяется аналогично. Область определения
определяется аналогично. Область определения  - множество всех чисел, где
- множество всех чисел, где  .
.
Построение графика: проведем касательную 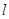 к единичной окружности в точке
к единичной окружности в точке  .
.

Пусть  произвольное число, для которого
произвольное число, для которого  . Тогда точка
. Тогда точка  не лежит на оси ординат, и, следовательно, прямая
не лежит на оси ординат, и, следовательно, прямая 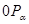 пересекает
пересекает  в некоторой точке
в некоторой точке 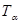 с абсциссой 1. Найдем ординату этой точки. Для этого заметим, что прямая
с абсциссой 1. Найдем ординату этой точки. Для этого заметим, что прямая  проходит через точки
проходит через точки  и
и  . Поэтому она имеет уравнение
. Поэтому она имеет уравнение 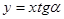 .
.
Абсцисса точки 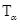 , лежащей на этой прямой, равна 1. Из уравнения прямой
, лежащей на этой прямой, равна 1. Из уравнения прямой  находим, что ордината точки
находим, что ордината точки 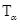 равна
равна  . Итак, ордината точки пересечения прямых
. Итак, ордината точки пересечения прямых  и
и 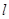 равна
равна  . Поэтому прямую
. Поэтому прямую 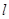 называют линией тангенсов.
называют линией тангенсов.


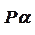


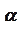
 Нетрудно доказать, что абсцисса точки
Нетрудно доказать, что абсцисса точки  пересечения прямой
пересечения прямой  с касательной m к единичной окружности, проведённой через точку
с касательной m к единичной окружности, проведённой через точку  , равна
, равна 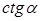 при
при  .
.
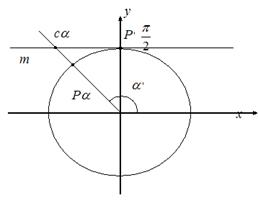
Поэтому прямую m называют линией котангенсов.
Область значений  - вся числовая прямая. Докажем это для функции
- вся числовая прямая. Докажем это для функции  . Пусть
. Пусть  - произвольное действительное число. Рассмотрим точку
- произвольное действительное число. Рассмотрим точку  . Как только что было показано,
. Как только что было показано,  равен
равен  . Следовательно, функция
. Следовательно, функция  принимает любое действительное значение
принимает любое действительное значение  , ч.т.д.
, ч.т.д.
Построение графика аналогично построению  .
.
Можно построить схему, позволяющую изобразить график тригонометрических функций:
1) Начертить единичную окружность, горизонтальный диаметр которой служит продолжением оси  . Разделить её на равные части (например,16).
. Разделить её на равные части (например,16).
2) Для функции  выбираем отрезок
выбираем отрезок  , для функции
, для функции  -
-  и делим их на то же равное число частей.
и делим их на то же равное число частей.
3) По окружности находим соответствующее число значений этих функций.
4) Точки пересечения горизонтальных линий, отвечающих значениям функций и вертикальных линий, отвечающих значениям аргумента, представляют собой точки графика.