Тригонометрический материал изучается в школьном курсе в несколько этапов.
1) Функции тригонометрических функций для углов от 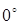 до
до 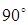
(прямоугольный треугольник, планиметрия);
2) Тригонометрические функции для углов от  до
до 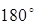 (тема: "Декартовы координаты на плоскости; геометрия");
(тема: "Декартовы координаты на плоскости; геометрия");
3) Тригонометрические функции для любого действительного числа.
Параллельно изучению теоретического материала учащиеся знакомятся с тригонометрическими формулами, объём которых будет постепенно рассширяться. Умение "выделить" эти формулы в дальнейшем поможет в преобразовании тригонометрических выражений.
К обязательным результатам обучения за курс геометрии в 7-9 классах относиться умение решать типичные задачи на вычисление значений геометрических величин (длин, углов, площадей) с привлечением свойств фигур, аппарата алгебры и тригонометрии.
Например:
1) В прямоугольном треугольнике найдите катеты, если его гипотенуза равна 5 см, а один из углов равен 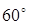 .
.
2) В прямоугольном треугольнике катет равен 4 см, а прилежащий к нему угол равен 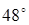 . Найдите другой катет и гипотенузу.
. Найдите другой катет и гипотенузу.
3) 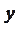
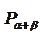 В треугольнике ABC: AB=3см, BC=6 см,
В треугольнике ABC: AB=3см, BC=6 см, 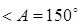 . Определите
. Определите  .
.
4) В треугольнике ABC известны стороны: AB=4 см; BC=5 см; AC=6 см.
 Найдите угол B.
Найдите угол B.
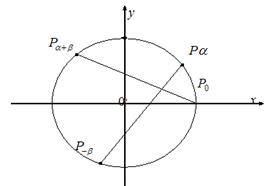
Существуют различные доказательства формулы косинуса суммы двух аргументов.
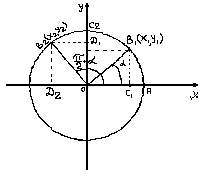
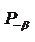 Одно из наиболее простых доказательств основано на применении системы координат и формулы расстояние между двумя точками. Воспроизвести доказательство по опорному конспекту:
Одно из наиболее простых доказательств основано на применении системы координат и формулы расстояние между двумя точками. Воспроизвести доказательство по опорному конспекту:
1. 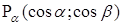 ;
;
2. 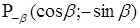 ;
;
3. 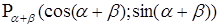 ;
;
4. 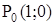 ;
;
5. 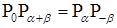 .
.
6. 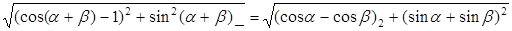 ;
;
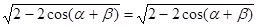 , ч.т.д.
, ч.т.д.
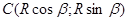 ;
; 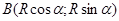 è
è 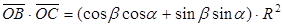 .
.
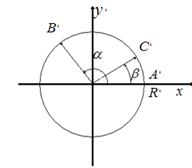
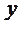 С другой стороны:
С другой стороны:
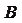
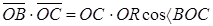 è
è
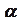
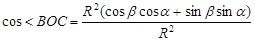 è
è 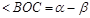 è
è
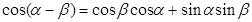 - теорема сложения.
- теорема сложения.
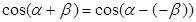
и по доказанной формуле.
Для доказательства  суммы и разности двух углов используются формула приведения, которые помогают преобразовать функции от аргументов вида:
суммы и разности двух углов используются формула приведения, которые помогают преобразовать функции от аргументов вида:
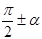 ,
, 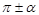 ,
, 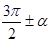 ,
, 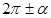 .
.
Проведём радиус 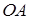 , длина которого равна
, длина которого равна 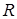 , на угол
, на угол 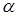 : и получили радиус
: и получили радиус 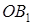 , где
, где 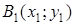 и на угол
и на угол 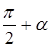 и получим радиус
и получим радиус 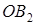 , где
, где 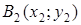 .
.
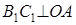 ,
, 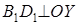 :
: 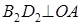 ,
, 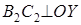 .
.
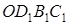 - прямоугольник. Повернём его на угол
- прямоугольник. Повернём его на угол 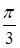 вокруг точки
вокруг точки 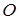 :
:
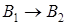 ;
;  ;
; 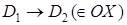 , т.е.
, т.е.
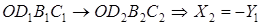 ;
; 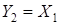 , т.е:
, т.е:
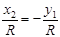 ;
; 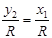 , по
, по 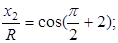
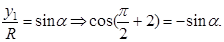
Аналогично:
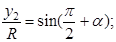

Тогда:
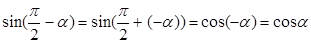
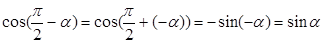
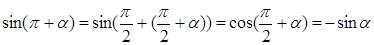
и т.д.
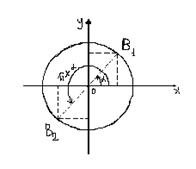
К функциям от углов 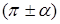 можно прийти и из геометрических соображений.
можно прийти и из геометрических соображений.
Формулы приведения для  и
и 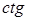 выводится из определения этих функций и ранее полученных формул приведения для синуса и косинуса. После этого полученные результаты сводятся в одну таблицу, с помощью которой можно сформулировать мнемоническое правило. Желательно учащимся предложить алгоритм применения формул приведения. Поясним его на примере:
выводится из определения этих функций и ранее полученных формул приведения для синуса и косинуса. После этого полученные результаты сводятся в одну таблицу, с помощью которой можно сформулировать мнемоническое правило. Желательно учащимся предложить алгоритм применения формул приведения. Поясним его на примере:
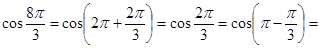 {определяем четность, в которой оканчивается угол
{определяем четность, в которой оканчивается угол 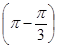 - II четверть; определяем знак данной функции в этой четверти – " - ". Изменяется ли название функции – нет, поэтому:}
- II четверть; определяем знак данной функции в этой четверти – " - ". Изменяется ли название функции – нет, поэтому:} 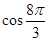 = - cos
= - cos 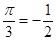 .
.
Вернёмся к выводу формулы синуса суммы и разности двух углов.
 ,
,
а затем применяется уже известная формула.
Формулы двойного угла выводятся из формулы синуса и косинуса суммы и разности двух углов, положив 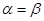 .
.
Сумму и разность тригонометрических функций можно преобразовать в произведение, используя следующий пример:
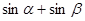 ={
={ 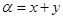 ,
, 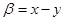 }=
}=
= 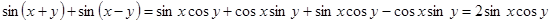 ,
,
но:
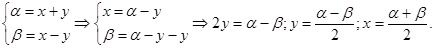
Таким образом:
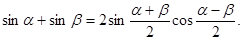
Замечание: при ознакомлении учащихся с формулами следует добиваться от них проговаривания словесных формулировок доказываемых формул.
Например: сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус полуразности.
В курсе алгебры 9 класса изучается тема: "Элементы тригонометрии" (30 часов):
1) радианное измерение углов, sin, cos, tg произвольного угла, их нахождение с помощью калькулятора;
2) основные тригонометрические тождества:
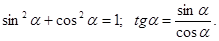
Их применение для вычисления значений sin, cos, tg;
3) формулы приведения; sin, cos суммы и разности двух углов; sin и cos двойного угла;
4) тождественные преобразования тригонометрических выражений; основная цель – сформировать умения выполнять тождественные преобразования несложных тригонометрических выражений с использованием формул, указанных в программе:
Рассмотрим некоторые примеры преобразований тригонометрических выражений:
Задача №1.
Доказать тождество:
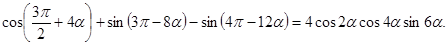
Преобразуем левую часть и получим, применив формулы приведения:
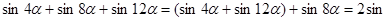 8
8  cos4
cos4  +sin8
+sin8 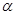 =2sin8
=2sin8 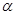 cos4
cos4 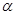 +2sin4
+2sin4  cos4
cos4  =2cos4
=2cos4  (sin8
(sin8  +sin4
+sin4  )=4cos4
)=4cos4  sin6
sin6  cos2
cos2  , и т.д.
, и т.д.
Задачи №2.
Упростить выражение
а) 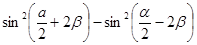
Можно применить формулы понижения степени:
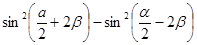 =
= 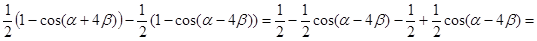
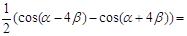 {воспользуемся преобразованием разности косинусов в произведение по формуле:
{воспользуемся преобразованием разности косинусов в произведение по формуле: 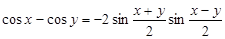 } =
} =
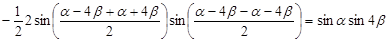
б) 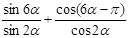
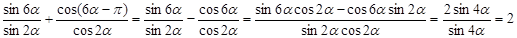
Задача №3
Преобразовать в произведение:
а) cos5  +sin8
+sin8  +cos9
+cos9  +cos12
+cos12  =(cos5
=(cos5  +cos12
+cos12  )+(cos8
)+(cos8  +cos9
+cos9 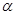 )=
)=
=2cos17/2  cos7/2
cos7/2  +2cos17/2
+2cos17/2  cos
cos  /2=2cos17/2
/2=2cos17/2  (cos7/2
(cos7/2  +cos
+cos 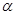 /2)=
/2)=
=4cos17/2  cos2
cos2  cos3/2
cos3/2  =4cos3/2
=4cos3/2  cos2
cos2  cos17/2
cos17/2 
б) 3+4cos4  +cos8
+cos8  =3(1+cos4
=3(1+cos4  )+(cos4
)+(cos4  +cos8
+cos8  )=6cos22
)=6cos22  +
+
+2cos6  cos2
cos2  =2 cos2
=2 cos2  (3cos2
(3cos2  +cos6
+cos6  )=2cos2
)=2cos2  ((cos2
((cos2  +|cos6
+|cos6 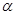 )+
)+
+2cos2  )=2cos2
)=2cos2  (2cos4
(2cos4  cos2
cos2  +2cos2
+2cos2  )=4cos22
)=4cos22  (cos4
(cos4  +cos2
+cos2 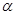 )=
)=
=4cos22  cos22
cos22  =8cos42
=8cos42 
Задача №4
Найти sin4  +cos4
+cos4  , если известно, что:
, если известно, что:
sin  -cos
-cos  =1/2
=1/2
sin4  +cos4
+cos4  =(sin2
=(sin2  +cos2
+cos2  )2-2sin2
)2-2sin2  cos2
cos2  =1-2sin2
=1-2sin2  cos2
cos2  =
=
=1-1/2sin22  ={sin4
={sin4  -cos
-cos  =1/2
=1/2 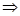 (sin
(sin  -cos
-cos  )2=
)2=
=1-2sin  cos
cos  =1/4
=1/4 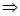 sin2
sin2  =3/4}=
=3/4}= 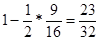
Задача №5
Вычислить:
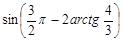
sin 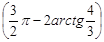 =-cos(2arctg4/3)={обозначим arctg4/3 через y, тогда получим cos2y, который нужно преобразовать в тангенс половинного угла. Применим формулу
=-cos(2arctg4/3)={обозначим arctg4/3 через y, тогда получим cos2y, который нужно преобразовать в тангенс половинного угла. Применим формулу 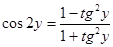 и получим}=
и получим}= 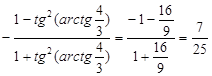
Заключение
Определенные трудности в изучение элементов тригонометрии (по Пифагору) порождает теорема: "Косинус угла α зависит только от градусной меры угла". Необходимость изучения данной теоремы можно разъяснить учащемуся так: Пусть требуется на основании определения найти cos 370. Предположим, что это задание выполняют отдельно друг от друга несколько человек. Чтобы найти cos 370, они построят прямоугольный треугольник (каждый свой) с углом в 370, измерят прилежащий катет и гипотенузу, найдут отношение прилежащего катета к гипотенузе. Полученное число и будет являться cos 370. Есть ли гарантия, что каждый ученик получит один и тот же ответ? Этот вопрос возникает по той причине, что каждый строит свой треугольник, получает свои значения длин прилежащего катета и гипотенузы. Так, может быть, и искомое отношение у каждого ученика будет какое-то свое? Понятно, что если бы значение cos 370 при переходе от одного прямоугольного треугольника к другому изменялось, то ценность такого понятия в математике была бы не велика. Изучаемая терема является ответом на поставленные вопросы. Она утверждает, что косинус острого угла зависит не от выбора прямоугольного треугольника, а только от меры угла.
Литература
1. К.О. Ананченко "Общая методика преподавания математики в школе", Мн., "Унiверсiтэцкае",1997г.
2.Н.М.Рогановский "Методика преподавания в средней школе", Мн., "Высшая школа", 1990г.
3.Г.Фройденталь "Математика как педагогическая задача",М., "Просвещение", 1998г.
4.Н.Н. "Математическая лаборатория", М., "Просвещение", 1997г.
5.Ю.М.Колягин "Методика преподавания математики в средней школе", М., "Просвещение", 1999г.
6.А.А.Столяр "Логические проблемы преподавания математики", Мн., "Высшая школа", 2000г.