Составное движение точки

З а д а н и е. Найти абсолютную скорость и абсолютное ускорение точки в момент времени t или в заданном положении.

x

 

 

Рис. 4.1.

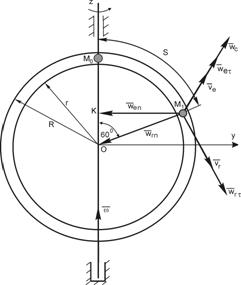
П р и м е р. Точка движется внутри кольца радиуса 0,2 м по закону 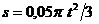, м (см. рис.4.1). В свою очередь, кольцо вращается вокруг своего диаметра в направлении, указанном на рисунке, с постоянным угловым ускорением .

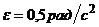В начальный момент кольцо находилось в покое,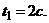

Р е ш е н и е. Проанализируем движение. Движение точки внутри кольца – относительное; движение, которое сообщает точке вращающееся кольцо, – переносное; движение точки относительно неподвижной Земли – абсолютное. Найдем положение точки на окружности в заданный момент времени, подставив в формулу относительного движения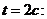

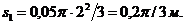
За 2 с точка в относительном движении описала дугу 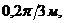которой соответствует центральный угол 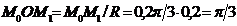рад, или 60⁰.

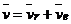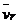Абсолютную скорость точки М найдем по теореме сложения скоростей , где и 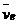- соответственно относительная и переносная скорости точки.

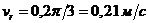Относительная скорость В момент времени t=2c . Эта скорость направлена по касательной к окружности кольца.

Переносная скорость 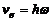, где h – кратчайшее расстояние от точки до оси вращения; ω – угловая скорость кольца.

Так как вращение по условию равнопеременное 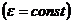, то угловая скорость 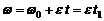, т.к. .

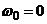Тогда 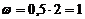рад/с. В свою очередь, 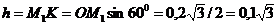м.

Это дает 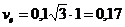м/с.

Переносная скорость перпендикулярна плоскости кольца и направлена от нас. Таким образом, 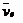^ 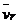, и модуль абсолютной скорости можно вычислить по теореме Пифагора: 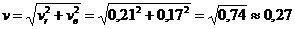м/с.

Абсолютное ускорение найдем по теореме Кориолиса

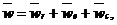(4.1)

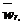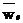где , и 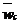- соответственно относительное, переносное ускорение и ускорение Кориолиса.

Относительное и переносное ускорения можно разложить на составляющие по касательным и нормалям к соответствующим траекториям (относительная и переносная траектории – окружности радиуса R с центром в точке О), т.е. , .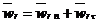

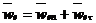Тогда равенство (4.1) примет вид:

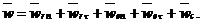(4.2)

Нормальное относительное ускорение =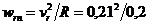

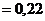м/с², вектор 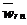направлен по радиусу 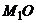к центру.

Касательное относительное ускорение 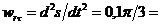= 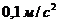, вектор 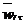направлен по касательной к окружности кольца, как показано на рис. 4.1.

Нормальное переносное ускорение 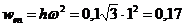м/с², вектор 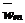направлен по 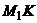к оси вращения. Касательное переносное ускорение 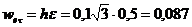м/с², вектор 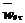перпендикулярен плоскости кольца и направлен от нас.

Ускорение Кориолиса 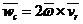. Модуль этого ускорения 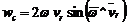. Вектор 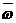направлен по оси вращения вверх, поэтому 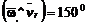. Тогда 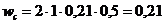м/с², вектор 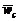перпендикулярен плоскости кольца и направлен от нас.

Введем систему координат, связанную с вращающимся кольцом, причем плоскость 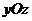совместим с плоскостью кольца, ось 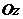направим по оси вращения, а ось 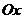- перпендикулярно плоскости кольца, к нам. Спроектируем теперь равенство (4.2) на выбранные оси:

 

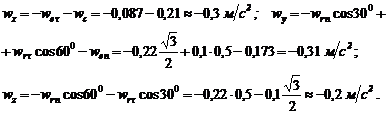
Отсюда

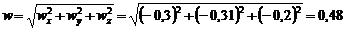м/с².

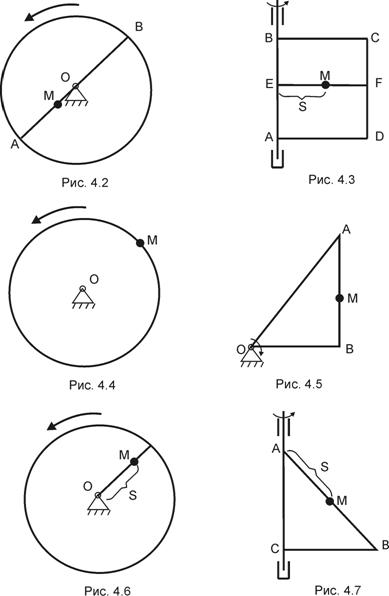
З а д а ч а 4.1. Горизонтальная платформа радиусом 0,5 м вращается равноускоренно с угловым ускорением 0,25 рад/c² из состояния покоя. В момент начала вращения из положения А выходит из состояния покоя движется равноускоренно в направлении АВ с относительным ускорением 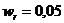м/с²; 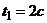(рис. 4.2).

З а д а ч а 4.2. Прямоугольная пластинка ABCD вращается вокруг стороны АВ по закону 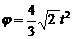рад. Вдоль EF (EF^ AB) движется точка по закону 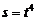м; 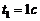(рис. 4.3).

 

З а д а ч а 4.3. Диск радиусом 1 м вращается равноускоренно из состояния покоя с угловым ускорением 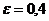рад/с². По ободу диска в сторону, противоположную направлению вращения, движется точка М по закону 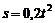м; 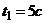(рис. 4.4).

 

З а д а ч а 4.4. Равнобедренный прямоугольный треугольник, катет которого равен 1 м, вращается вокруг вершины О равноускоренно из состояния покоя с угловым ускорением 3 рад/с². В момент начала вращения из вершины А выходит точка с начальной относительной скоростью 2,5 м/с и движется по катету АВ с постоянным ускорением 3 м/с²; 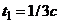(рис. 4.5).

 

З а д а ч а 4.5. Диск вращается равноускоренно из состояния покоя с угловым ускорением 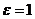рад/с². По радиусу диска движется точка по закону 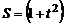м; 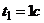(рис. 4.6).

 

З а д а ч а 4.6. Решить задачу 4.3 при условии, что точка движется в сторону вращения, а 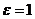рад/с², 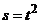м, 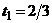с (рис. 4.4).

 

З а д а ч а 4.7. Равнобедренный прямоугольный треугольник вращается вокруг своего катета равноускоренно из состояния покоя с угловым ускорением 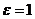рад/с². Точка движется по гипотенузе согласно закону 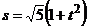м; 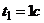(рис. 4.7).

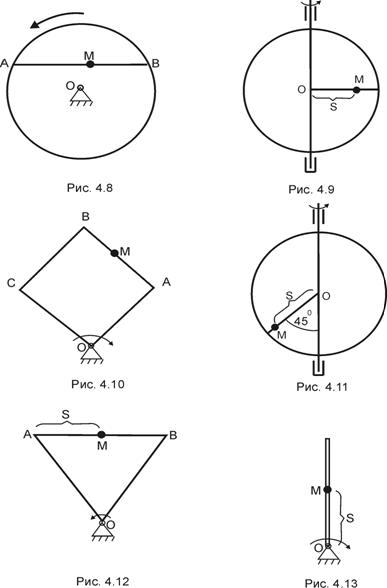
З а д а ч а 4.8. Диск радиусом 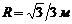и вращается равноускоренно с угловым ускорением 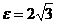рад/с². По стороне АВ вписанного равностороннего треугольника движется точка с постоянным относительным ускорением 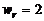м/с². Найти абсолютную скорость и абсолютное ускорение точки в момент, когда она придет в положение В, если в этот момент 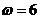рад/с и 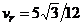м/с (рис. 4.8).

 

З а д а ч а 4.9. Диск вращается равноускоренно из состояния покоя вокруг своего диаметра с угловым ускорением 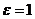рад/с². По радиусу диска из центра движется точка по закону 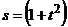м; 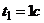(рис. 4.9).

 

З а д а ч а 4.10. Квадрат со стороной 1 м равноускоренно вращается вокруг своей вершины О с угловым ускорением 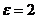рад/с². По стороне АВ движется точка с постоянным относительным ускорением 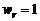м/с². Найти абсолютную скорость и абсолютное ускорение точки в момент, когда она достигнет вершины В, если в этот момент 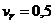м/с, а 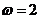рад/с (рис. 4.10).

 

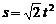З а д а ч а 4.11. Круглая пластинка вращается вокруг своего диаметра по закону рад. По радиусу ОА движется точка по закону м; 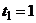с (рис. 4.11).

 

З а д а ч а 4.12. Равносторонний треугольник со стороной 1 м вращается вокруг своей вершины О по закону 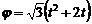рад. По стороне АВ движется точка по закону 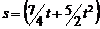м; 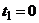(рис. 4.12).

 

З а д а ч а 4.13. Полая трубка вращается равноускоренно из состояния покоя в плоскости чертежа с угловым ускорением 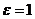рад/с². Внутри трубки движется точка по закону 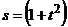м; 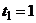с (рис. 4.13).

З а д а ч а 4.14. Квадрат со стороной 1 м вращается равноускоренно с угловым ускорением 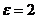рад/с² вокруг центра О. По стороне АВ движется точка с постоянным относительным ускорением 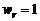м/с². Найти абсолютную скорость и абсолютное ускорение точки в момент, когда она достигнет положения В, если в момент 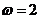рад/с, момент 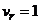м/с (рис. 4.14).

 

 

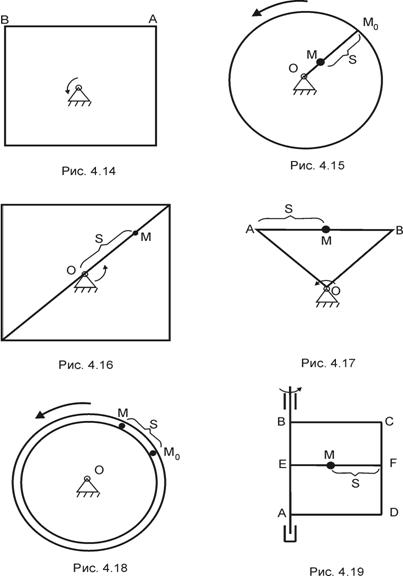
З а д а ч а 4.15. Диск радиусом 0,6 м вращается по закону 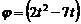рад вокруг оси О. К центру по радиусу диска движется точка по закону 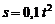м; 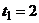с (рис. 4.15).

 

З а д а ч а 4.16. Квадрат вращается вокруг своего центра О по закону 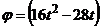рад. По диагонали квадрата движется точка по закону 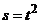м; 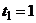с (рис. 4.16).

 

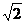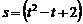З а д а ч а 4.17. Равнобедренный прямоугольный треугольник, катет которого равен м вращается без начальной угловой скорости с постоянным угловым ускорением рад/с² вокруг вершины О. По гипотенузе движется точка по закону м; 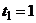с (рис. 4.17).

 

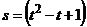З а д а ч а 4.18. Полное кольцо радиусом R = 1 м вращается без начальной угловой скорости вокруг оси О с постоянным угловым ускорением рад/с². Внутри кольца движется точка по закону м; 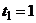с (рис.4.18).

 

З а д а ч а 4.19. Прямоугольная пластинка ABCD вращается вокруг стороны АВ по закону 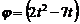рад. Вдоль FE (FE^ AB) движется точка по закону 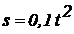м. Ширина пластинки ВС = 0,6 м; 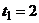с (рис.4.19).

 

З а д а ч а 4.20. Равнобедренный треугольник вращается вокруг гипотенузы АС без начальной угловой скорости с постоянным угловым ускорением 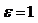рад/с². По катету АВ движется точка по закону 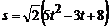м; 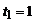с (рис. 4.20).

 

З а д а ч а 4.21. Круглый диск радиусом 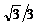м вращается равноускоренно без начальной угловой скорости с угловым ускорением 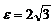рад/с². По стороне АВ вписанного шестиугольника движется точка по закону 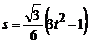м; 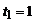с (рис. 4.21).

 

З а д а ч а 4.22. Решить задачу 4.18, предполагая, что точка движется в сторону, противоположную направлению вращения; 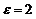рад/с²; R = 1 м; 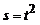м (см. рис.4.18).

З а д а ч а 4.23. Кривошип ОА длиной 0,6 м вращается по закону 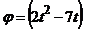рад. Вдоль кривошипа от А к О движется точка по закону 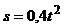м; 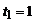с (рис.4.22).

 

З а д а ч а 4.24. Круглый диск радиусом 1,5 м вращается в плоскости чертежа вокруг оси О по закону 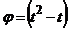рад. По диаметру АВ движется точка по закону 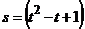м; 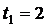с (рис.4.23).

 

З а д а ч а 4.25. Равносторонний треугольник со стороной 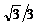м вращается равноускоренно без начальной угловой скорости с угловым ускорением 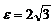рад/с². По стороне АВ движется точка по закону 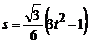м; 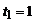с (рис. 4.24).

 

З а д а ч а 4.26. Квадрат со стороной 1 м равноускоренно вращается вокруг своей вершины О с угловым ускорением 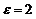рад/с². По стороне АВ движется точка с постоянным относительным ускорением 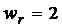м/с². Найти абсолютную скорость и абсолютное ускорение точки в момент, когда она достигнет вершины В, если в этот момент 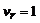м/с, а 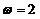рад/с (рис. 4.25).

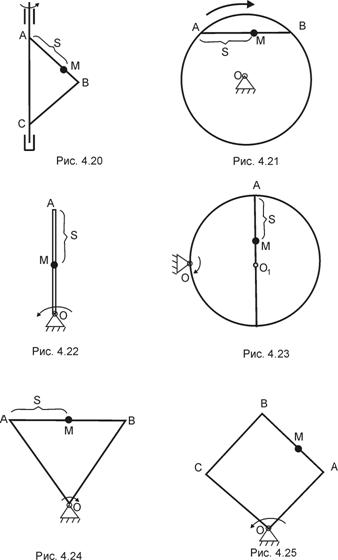
З а д а ч а 4.27. Прямоугольный треугольник вращается вокруг своего катета АС по закону 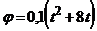рад. По гипотенузе АВ по закону 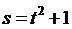м движется точка; 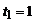с (рис. 4.26).

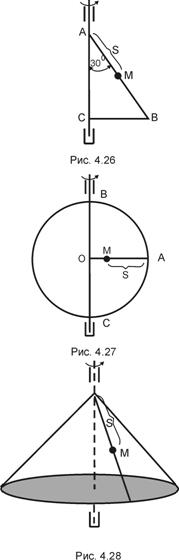
З а д а ч а 4.28. Диск радиусом 0,6 м вращается по закону 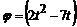рад вокруг своего диаметра. По радиусу ОА диска (АО^ВС) от А к центру движется точка по закону 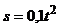м; 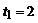с (рис.4.27).

 

З а д а ч а 4.29. Конус, имеющий прямой угол при вершине, вращается вокруг своей оси по закону 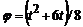рад. По образующей конуса движется точка по закону 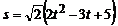м; 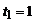с (рис.4.28).

 

З а д а ч а 5.30. Решить задачу 4.24 в предположении, что направление вращения диска изменилось на противоположное (см. рис. 4.23).