2.1. Методические указания к первому занятию по методу наименьших квадратов
Для получения искомой зависимости y=f(x) по имеющимся экспериментальным точкам (xi, yi) обычно пользуются методом наименьших квадратов. В этом случае задача состоит в том, чтобы сумма квадратов отклонений экспериментальных точек от сглаживающей кривой обращалась в минимум *:
. (2.1)
Здесь xi, yi - экспериментальные значения переменных в i-том опыте; N - количество опытов, N>S, где S - число коэффициентов искомой зависимости.
При выборе вида зависимости y=f(x) возможны следующие случаи:
1. Общий вид зависимости y=f(x) известен заранее на основании теоретических предпосылок. Задача состоит в нахождении числовых значений параметров этой зависимости.
2. Зависимость y=f(x) неизвестна и нет никаких предположений о ее математической форме. В этом случае для эмпирического описания исследуемой закономерности в области ее существования, ограниченной пределами изменения аргумента, удобно применить алгебраический полином определенной степени.
Рассмотрим методику определения числовых значений параметров y=f(x), удовлетворяющих условию (2.1). При этом будем считать, что вид функции f(x), зависящей от нескольких параметров a l, l =1, 2, 3... известен. Запишем y как функцию не только аргумента x, но и параметров a1, a2, a3,…, т.е.
y=f(x, a1, a2, a3,…).
Найдем значения al, при которых левая часть выражения (2.1) обращается в минимум. Для этого продифференцируем его по переменной al и приравняем производные к нулю. Тогда получим:
,
 |
* Строго говоря, данное утверждение справедливо при равноточных измерениях и нормальном законе распределения погрешностей.
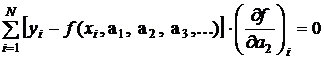; (2.2)
.
и т.д.
Здесь 
- значение частной производной функции f по параметру al в точке х=xi, y=yi.
Система уравнений (2.2) содержит столько же уравнений, сколько и неизвестных коэффициентов a1, a2, a3,…. Решить эту систему в общем виде нельзя – надо знать конкретный вид функции f. В случае, когда эта функция задана в виде алгебраического полинома, система уравнений (2.2) получается линейной относительно искомых коэффициентов полинома. Ее обычно называют нормальной.
Если y является функцией нескольких аргументов, процедура нахождения параметров al в принципе не меняется. В уравнение (2.2) подставляются те сочетания аргументов, которые имели место в i-том опыте.
Рассмотрим методику проведения эксперимента, когда искомая зависимость y=f(x) может быть представлена в линейном виде:
y = a0 + a1x. (2.3)
Для нахождения коэффициентов a0 и a1 воспользуемся методом наименьших квадратов, согласно которому задача вычисления числовых значений коэффициентов сводится к отысканию экстремума функции двух переменных a0 и a1:
. (2.4)
Взяв частные производные от S2 по переменным a0 и a1 и приравняв их к нулю, получим систему нормальных уравнений
;
(2.5)
.
Решение системы (2.4) дает значение искомых коэффициентов.
2.2 Примеры к первому практическому занятию
Пример 2.1. При проведении экспериментальных исследований скоростной характеристики двигателя постоянного тока с независимым возбуждением получены следующие результаты:
| I, A | -10 | -7,5 | -5 | -2,5 | 2,5 | 5,0 | 5,0 | 7,5 | ||
| w, c-1 |
Согласно теоретическим данным зависимость скорости двигателя от тока якоря описывается следующим уравнением
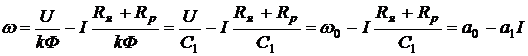. (2.5)
Здесь w, w0 = а0 – угловые значения текущей скорости и скорости идеального холостого хода, с-1; U - напряжение сети, В; I - ток якоря, А; Rя, Rр - сопротивление якоря и дополнительное сопротивление якорной цепи, Ом; Ф - магнитный поток двигателя, Вб; К - конструктивная постоянная машины, В×с/Вб; С1 – коэффициент, В×с (Н×м/А).
При неизменных U, Ф и R (условие проведения эксперимента) эта зависимость линейна, а ее характеристика прямая линия. Определим коэффициенты a0, a1 уравнения (2.5). Для нахождения коэффициентов a0, и a1 воспользуемся методом наименьших квадратов (используем для определения искомых коэффициентов систему уравнений (2.4)). В рассматриваемом случае она примет вид
;
(2.6)
.
Решение системы (2.6) дает значение искомых коэффициентов.
В рассматриваемом случае в соответствии с результатами эксперимента
Подставив эти значения в (2.6), найдем а0=146,5 с-1; и а1=4,262 (А×с)-1. Тогда зависимость w=f(I) примет вид
w = 146,5 - 4,262×I.
Аппроксимирующая прямая и экспериментальные точки приведены на рис. 2.1.
Рисунок 2.1
Пример 2.2. При проведении экспериментальных исследований скоростной характеристики двигателя постоянного тока последовательного возбуждения получены следующие результаты:
| I, A | ||||||||
| w, c-1 |
Скоростная характеристика двигателя описывается уравнением
.
Здесь 
- сопротивление последовательной обмотки возбуждения; а - коэффициент, определяющий наклон начального (до насыщения) участка кривой намагничивания.
Используя результаты эксперимента выразим зависимость w=f(I) в виде:
. (2.7)
Для нахождения коэффициентов а0 и а1 воспользуемся методом наименьших квадратов. Определим частные производные функции (2.7) по переменным аi
; 
.
После подстановки этих значений в систему уравнений (2.2) получим:
;
(2.8)
.
В данной задаче N=8; 
=1237 c-1;
Подставив эти значения в (2.8), найдем
a0 = 46,2 с-1; a1 = 1000 A/c.
Уравнение искомой скоростной характеристики
.
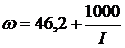Используя полученное уравнение, рассчитаем скоростную характеристику двигателя. При расчете задаемся значениями тока, которые соответствуют эксперименту. После подстановки этих значений в уравнение скоростной характеристики определяем значение угловой скорости. Получены следующие результаты:
| I, A | ||||||||
| w, c-1 | 84,0 |
Аппроксимирующая кривая и экспериментальные точки приведены на рис. 2.2.
Рисунок 2.2
Пример 2.3. При пуске без нагрузки двигателя постоянного тока независимого возбуждения в определенные моменты времени ti была измерена с помощью таховольтметра угловая скорость двигателя. Данные эксперимента приведены ниже:
| ti, c | ||||||||
| w, c-1 |
Требуется определить электромеханическую постоянную времени двигателя.
При пуске двигателя без нагрузки зависимость скорости от времени описывается уравнением:
.
Здесь w0 - установившееся значение скорости, равное скорости идеального холостого хода, w0=100 с-1; Тм - искомый параметр, электромеханическая постоянная времени привода.
При попытке использовать приведенную зависимость w=f(t) для определения электромеханической постоянной времени двигателя с помощью метода наименьших квадратов возникает необходимость решения нелинейного уравнения. Однако в рассматриваемом случае можно исключить решение нелинейного уравнения, преобразовав искомое уравнение. Выполним эти преобразования.
;
или
;
.
Для определения электромеханической постоянной времени воспользуемся рассматриваемой методикой и применим ее для последнего уравнения:
. (2.9)
Здесь 
.
Решение уравнения (2.9) позволяет определить значение электромеханической постоянной времени двигателя
.
В рассматриваемом случае в соответствии с результатами эксперимента получим:
| t, c | ||||||||
| 0,301 | 1,723 | 3,587 | 9,163 | 18,06 | 42,41 | 105,2 | |
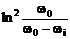
| 0,0227 | 0,186 | 0,357 | 0,84 | 1,45 | 4,5 | 12,3 |
Определим как зависит значение Тм от количества экспериментальных значений исследуемой зависимости. Результаты расчета сведем в следующую таблицу:
| N | |||||||
| 0,301 | 2,024 | 5,611 | 14,774 | 32,834 | 75,244 | 180,444 |
| 0,0227 | 0,2087 | 0,5657 | 1,4057 | 2,8557 | 7,3557 | 19,66 |
| Тм, с | 13,26 | 9,7 | 9,92 | 10,51 | 11,5 | 10,23 | 9,18 |
Таким образом, наилучшим приближением к опытным данным будет уравнение
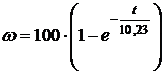, с-1 .
Аппроксимирующая кривая зависимости w=f(t) и экспериментальные точки для N=7, Tм=10,23 с показаны на рис. 2.3.
Рисунок 2.3
Пример 2.4. При отключении обмотки возбуждения генератора постоянного тока от источника питания и замыкании его на разрядный резистор в определенные моменты времени ti была измерена с помощью цифрового прибора сила тока возбуждения ii. Данные эксперимента приведены ниже:
| ti, c | |||||||||||
| ii, A |
Измерение силы тока производилось с погрешностью Di=±5 A.
Зависимость силы тока возбуждения от времени имеет вид:
. (2.10)
Здесь I0 - начальная сила тока, I0=100 А; Тв - искомый параметр, Тв= 
, где rв, rр - электрические сопротивления обмотки возбуждения и разрядного резистора; Lв - индуктивность обмотки возбуждения.
На основе опытных данных определим в первом приближении значение Тв. Известно, что функция e-x при х=3 достигает значения, примерно равного 0,05. Тогда, как видно из данных эксперимента, при t=9¸10 с значение I=0,05I0 и, следовательно, постоянная времени примерно равна Тв=t/3»3-3,3 c. Для уточнения Тв воспользуемся методом наименьших квадратов. Зададимся несколькими значениями Тв, близкими к 3 с. Затем по формуле (2.10) вычислим силу тока Ii в точках t=ti. В соответствии с (2.2) определим значение суммы квадратов отклонений 
= S2 для различных значений Тв. Оформим результаты вычислений:
| Тв, c | 3,03 | 3,125 | 3,226 | 3,33 | 3,45 | 3,57 |
| S2, A | 51,4 | 25,7 | 13,6 | 17,4 | 40,3 | 83,3 |
Построив график функции S2=j(Тв) (рис. 2.4) найдем, что S2=min при Тв=3,22 с.
Таким образом, наилучшим приближением к опытным данным является функция
.
График этой функции и экспериментальные точки показаны на рис. 2.5.
Рисунок 2.4
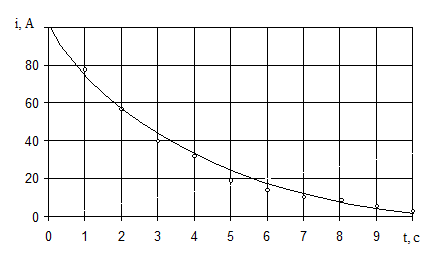
Рисунок 2.5
2.3 Задачи на самостоятельную проработку на первом практическом занятии
Задача 2.1. При проведении экспериментальных исследований скоростной характеристики двигателя постоянного тока с независимым возбуждением получены данные, приведенные в табл. 2.1. Используя метод наименьших квадратов, определить параметры уравнения скоростной характеристики двигателя постоянного тока параллельного возбуждения w=f(t).
Таблица 2.1
| Номер точки экспери-мента | Первая цифра варианта, Ток двигателя, А | Вторая цифра варианта, Угловая скорость, с-1 | ||||||||
| -12 | -16 | -8 | -13 | -5 | ||||||
| -8 | -10 | -5 | -9 | -3 | ||||||
| -4 | -5 | -2,5 | -4,5 | -1,5 | ||||||
| 5,5 | 2,5 | |||||||||
Задача 2.2. При проведении экспериментальных исследований скоростной характеристики двигателя постоянного тока с последовательным возбуждением получены данные, приведенные в табл. 2.2. Используя метод наименьших квадратов, определить параметры уравнения скоростной характеристики двигателя w=f(t).
Таблица 2.2
| Номер точки экспери-мента | Первая цифра варианта, Ток двигателя, А | Вторая цифра варианта, Угловая скорость, с-1 | ||||||||
| 20,1 | 73,5 | |||||||||
| 40,2 | ||||||||||
| 60,3 | ||||||||||
| 80,4 | ||||||||||
| 100,5 | ||||||||||
| 120,6 | ||||||||||
| 140,7 | ||||||||||
| 160,8 |
Задача 2.3. При пуске без нагрузки двигателя постоянного тока независимого возбуждения в определенные моменты времени t была измерена с помощью таховольтметра угловая скорость двигателя. Требуется определить электромеханическую постоянную времени двигателя. Данные эксперимента приведены в табл. 2.3.
Таблица 2.3
| Номер точки экспери-мента | Первая цифра варианта, Моменты времени ti, c | Вторая цифра варианта, Угловая скорость, с-1 | ||||||||
| 0,02 | ||||||||||
| 0,1 | 0,025 | 0,2 | 0,5 | |||||||
| 0,2 | 0,05 | 0,4 | ||||||||
| 0,3 | 0,075 | 0,6 | 1,5 | |||||||
| 0,4 | 0,1 | 0,8 | ||||||||
| 0,5 | 0,125 | |||||||||
| 0,6 | 0,15 | 1,5 | ||||||||
| 0,7 | 0,2 | |||||||||
| 0,8 | 0,25 | 2,5 | ||||||||
| 0,3 |
2.4 Методические указания ко второму занятию по методу наименьших квадратов
Статическая оценка результатов аппроксимации.
1. Дисперсия воспроизводимости.
, (2.11)
где m - число параллельных опытов в i-й точке,
j - порядковый номер параллельного опыта в i-й точке.
Обычно критерием равноточности служит отношение максимальной дисперсии в соответствующей опытной точке Dyмакс к сумме всех дисперсий в N опытных точках:
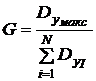. (2.12)
Полученное значение G сравнивается с табличным GT (см. приложение 2), определенным для числа степеней свободы m-1, N при принятом уровне значимости (чаще всего равном 0,05). Если G<GT, то гипотеза о равноточности не отвергается.
Дисперсия опыта (средняя дисперсия математических ожиданий)
. (2.13)
Здесь mN=n - общее число измерений.
2. Оценка адекватности аппроксимирующей зависимости исследуемому объекту обычно производится с помощью критерия Фишера
. (2.14)
Здесь Dya остаточная дисперсия, равная
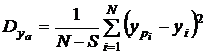, (2.15)
где S - количество искомых параметров аппроксимирующей зависимости; ypi - расчетное значение функции в i-й точке при аппроксимации ее зависимостью вида y=f(x1, x2,..).
Полученное значение F сравнивается с табличным FT (см. приложение 1), определенным для степеней свободы r1=N-S; r2=N(m-1) при принятом уровне значимости. Если F<FT, то гипотеза от адекватности не отвергается. Если погрешность опыта 
известна априори, то при 
£ модель адекватна.
3. Оценка значимости коэффициентов аппроксимирующей зависимости, взятой в виде алгебраического полинома.
Оценку проводят для каждого коэффициента al с помощью критерия Стьюдента
. (2.16)
Здесь 
, где Dal - дисперсия коэффициента регрессии al.
Величины Dal определяем следующим образом. Правые части уравнений (2.4) 
не заменяются их числовыми значениями. В результате решения (2.4) для коэффициентов al находятся линейные зависимости от величины vi. Если в эти уравнения (2.4) подставить вместо vi единицу, а вместо al значение Ml, с помощью которого и находят Dal:
, (2.17)
где определяется по (2.13).
Значение tl, определенное по формуле (2.15), сравнивается с табличным, найденным для числа степеней свободы r =N(m-1) при принятом уровне (см. приложение 3) значимости. Если tl>tT, коэффициент al считается незначимым (т.е. можно принять al=0) и соответствующее слагаемое исключается из уравнения регрессии. При m=1 имеем v=0 и рассматриваемый метод оценки неприменим. В этом случае оценка значимости коэффициента может быть произведена путем сравнения дисперсий адекватности Dya при наличии члена аппроксимирующего полинома с коэффициентом al и при его отсутствии. Если дисперсия для второго варианта близка к дисперсии для первого (или меньше), то рассматриваемый коэффициент можно считать незначимым.
2.5 Примеры ко второму занятию по методу наименьших квадратов
Пример 2.5. Для условий, указанных в примере 2.1, проверить адекватность полученной зависимости w=146,5–4,262I при дисперсии опыта 
=25 1/c2 и числе параллельных измерений в каждой точке m=3.
По данным эксперимента вычислим дисперсию адекватности
.
Так как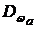 
> 
, для оценки адекватности определим значение критерия Фишера: F= 
=53/25=2,12.
Значение FT, установленное по табл.2.4, при степенях свободы r1= N-S = =10–2=8, r2=N(m-1)=10(3-1)=20 равно 2,45. Следовательно, F<FT и найденная зависимость адекватно описывает исследуемое явление.
Таблица 2.4 - Значения критерия Фишера FT при уровне значимости 0,05
| r2 | r1 | ||||||||
| ¥ | |||||||||
| ¥ | 18,51 10,13 7,71 5,99 5,32 4,96 4,54 4,35 4,24 4,17 3,92 3,84 | 19,00 9,55 6,94 5,14 4,46 4,10 3,68 3,49 3,38 3,32 3,07 2,99 | 19,16 9,28 6,59 4,76 4,07 3,71 3,29 3,10 2,99 2,92 2,68 2,60 | 19,25 9,12 6,39 4,53 3,84 3,48 3,06 2,87 2,76 2,69 2,45 2,37 | 19,33 8,94 6,16 4,28 3,58 3,22 2,79 2,60 2,49 2,42 2,17 2,09 | 19,37 8,84 6,04 4,15 3,44 3,07 2,64 2,45 2,34 2,27 2,02 1,94 | 19,41 8,74 5,91 4,00 3,28 2,91 2,48 2,28 2,16 2,09 1,83 1,75 | 19,45 8,64 5,77 3,84 3,12 2,74 2,29 2,08 1,96 1,89 1,61 1,52 | 19,5 8,53 5,63 3,67 2,93 2,54 2,07 1,84 1,71 1,62 1,25 1,00 |
Пример 2.6. Необходимо на основании минимально возможного числа опытов определить аппроксимирующую зависимость w*=f(M*) относительной угловой скорости 
от величины относительного момента 
искусственной механической характеристики асинхронного двигателя в виде полинома функции.
В соответствии с (2.12) минимальное число опытных точек, при которых можно вычислить дисперсию адекватности 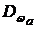, составляет Nмин=S+1. С увеличением N точность описания повышается, но стоимость эксперимента увеличивается. Будем считать достаточным количество опытов, при котором 
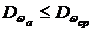, где 
- дисперсия опыта.
В общем случае, когда нет возможности предсказать степень аппроксимирующего полинома, эксперимент проводится в несколько этапов, число которых зависит от конкретного вида получаемой кривой. На этих этапах последовательно проверяется гипотеза о пригодности полиномов первого, второго и более высоких порядков в качестве уравнений, описывающих процесс.
Будем считать, что погрешность задания значений М* пренебрежимо мала, а погрешность измерения величины w* составляет 
=0,01. Величина М* изменяется в пределах Ммин<M<Ммакс, где Ммин=0, Ммакс=3.
В первой серии опытов аппроксимирующую зависимость будем искать в виде
.
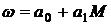При этом Nмин=3; S=2 (определяем 2 коэффициента a0 и a1).
Исследуемую область изменения момента разделим на два участка. Тогда шаг изменения момента
.
Для упрощения вычислений введем относительную величину
,
где М0 - начальное значение измеряемого параметра (момента). Если во всей исследуемой области изменения момента до проведения опыта нет причины предпочесть определенное значение М, то в качестве М0 можно взять среднюю точку М0=(Ммакс–Ммин)/2. В данном случае М0=1,5. Тогда
;
; 
.
Ставим опыты 1 – 3 при этих значениях х и результаты измерений w=wэ заносим в табл.2.5.
Для вычисления коэффициентов a0 и a1 воспользуемся методом наименьших квадратов, решив систему нормальных уравнений
;
.
В рассматриваемом случае 
; 
и, следовательно,
; 
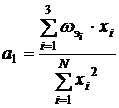. (2.14)
Заметим, что в данном случае коэффициенты а0 и а1 независимы, что резко упрощает вычислительные процедуры и позволяет рассчитать не зависящие друг от друга статистические оценки коэффициентов.
Таблица 2.5 – Данные эксперимента и результаты расчета
| № опыта i | Значение момента М* | Значение х | Экспериме- нтальное значение wэ | Расчетные значения критерия wр | Отклонение Dw=wэ–wр | |||||
| I серия S=2 | II серия | I серия S=2 | II серия | |||||||
| I серия | II серия | S=2 | S=3 | S=2 | S=3 | |||||
| -1 | -2 | 0,927 | 1,083 | 0,964 | 0,073 | -0,083 | 0,036 | |||
| 0,75 | - | -1 | 0,9 | - | 0,887 | 0,948 | - | 0,013 | -0,048 | |
| 1,5 | 0,78 | 0,647 | 0,691 | 0,812 | 0,133 | 0,089 | -0,022 | |||
| 2,25 | - | 0,62 | - | 0,495 | 0,556 | - | 0,125 | 0,064 | ||
| 0,16 | 0,367 | 0,299 | 0,18 | -0,207 | -0,139 | -0,02 |
Исходя из соотношений (2.14) и данных табл. 2.5, получаем а0=0,647; а1=-0,28. Тогда в первом приближении имеем
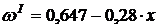. (2.15)
В соответствии с (2.15) определим расчетное значение wр и занесем его в табл. 2.5. Отклонения Dwi служат для проверки вычислений: 
0. Нанесем опытные точки и аппроксимирующую прямую на график (рис. 2.6). Даже визуальный анализ графика показывает, что опытные и расчетные точки значительно отстоят друг от друга.
При этом
,
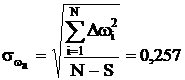и, следовательно, аппроксимация (2.15) неадекватно отражает изучаемую зависимость либо в силу каких-то причин результаты опытов оказались экстенсивными (резко отличающимися от средних). Последняя гипотеза маловероятна, так как Dwмакс<3 , но окончательно ее можно отвергнуть, лишь поставив дополнительные опыты.
Рисунок 2.6
Проведем II серию опытов (опыты 4 – 5), уменьшив шаг изменения параметра М (момента) вдвое, т.е. взяв N=5. Тогда DM=0,75. При заполнении табл. 2.5 учтем, что при изменении шага DM меняются и значения х. Принимая во внимание результаты I серии опытов, дополнительно ставим два опыта в точках М4=0,75 (x4=-1) и М5=2,25 (x=+1). Записав результаты этих опытов, по формулам (2.14) найдем коэффициенты полинома первой степени: а0=0,691 а1=-0,196. Тогда
. (2.16)
Определим в соответствии с уравнением (2.16) расчетные значения wpi для всех значений xi (табл. 2.5). Результаты расчета показывают, что существенного улучшения аппроксимации при увеличении количества опытов не получено (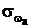
=0,129). В связи с этим перейдем к аппроксимации искомой зависимости полиномом второй степени:
. (2.17)
Отметим, что условие Nмин=S+1£N выполняется (S=3 - количество постоянных уравнения (2.17), N=5 - количество точек эксперимента). Коэффициенты полинома (2.17) вычислим, решив систему нормальных уравнений 2.18.
По данным табл. 2.5 для II серии опытов при S=3 имеем
; 
; 
; 
.
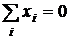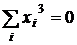В рассматриваемом случае независимым остается только коэффициент а1. Коэффициенты а0 и а2 зависимы.
;
; (2.18)
.
После подстановки данных эксперимента в уравнение (2.18) и решения системы уравнений найдем а0=0,812; а1=-0,196; а2=-0,06 и, следовательно,
. (2.19)
Значения wр, определенные в соответствии с (2.19), приведены в табл. 2.5. Анализ показывает, что аппроксимация искомой зависимости полиномом вида (2.17) дает существенно лучшие результаты. Значение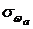 
снизилось до 0,0655, что меньше погрешности опыта =0,1. Это свидетельствует об адекватности расчетной и опытной зависимостей. Таким образом, опыты можно не продолжать.
Сформулируем некоторые общие моменты, вытекающие из последнего примера:
1. Введение относительного значения аргумента позволяет резко упростить вычислительные операции;
2. Каждая последующая серия опытов включает в себя результаты предыдущих опытов;
3. Дробление шага квантования по уровню нужно производить, деля шаг предыдущей серии на два, тогда последовательно обрабатываемые серии будут состоять из N=1+2l опытов, где l - номер серии;
4. На количество серий влияют конкретный вид зависимости и точность аппроксимации, которая, в свою очередь, ограничивается точностью измерения величины w в каждом опыте;
5. Все приведенные выше вычисления могут быть произведены с помощью ЭВМ по стандартным программам, что значительно сокращает объем вычислительных работ.
2.6 Задачи на самостоятельную проработку на втором занятии по методу наименьших квадратов
Задача 2.4. Для условий, указанных в задаче 2.1, проверить адекватность полученной зависимости w=f(I) при дисперсии опыта =10 1/c2 и числе параллельных измерений в каждой точке m=3.
Задача 2.5. На основании минимально возможного числа опытов определить аппроксимирующую зависимость w*=f(M*) относительной угловой скорости 
от величины относительного момента асинхронного двигателя в виде полинома функции w0=а0+а1М+а2М2=..... Погрешность измерения величины принять равной =0,1. Данные, необходимые для расчета, приведены в табл. 2.6.
Указание. Экспериментальную кривую зависимости w*=f(M*) разделить на два интервала:
1-й – w= 0¸wкр; 2-й – w= wкр¸1.
Каждый из этих двух отрезков экспериментальной кривой аппроксимировать с помощью полинома функции w0=а0+а1М+а2М2=..... Порядок полинома функции w0=f(M) определяется из следующего условия: 
(погрешность опыта не меньше погрешности аппроксимации).
Таблица 2.6
| Номер точки экспери-мента | Первая цифра варианта, Относительная угловая скорость двигателя w* | Вторая цифра варианта, Относительный момент М* | ||||||||
| 0,9 | 0,875 | 0,95 | 0,925 | 0,85 | 0,8 | 1,1 | 0,9 | 1,2 | ||
| 0,8 | 0,75 | 0,9 | 0,85 | 0,7 | 2,4 | 2,5 | 2,3 | 2,0 | 2,6 | |
| 0,7 | 0,625 | 0,85 | 0,775 | 0,55 | 2,8 | 2,9 | 2,7 | 2,4 | 2,9 | |
| 0,6 | 0,5 | 0,8 | 0,7 | 0,4 | ||||||
| 0,45 | 0,375 | 0,6 | 0,425 | 0,3 | 2,8 | 2,7 | 2,6 | 2,9 | 2,7 | |
| 0,3 | 0,25 | 0,4 | 0,35 | 0,2 | 2,4 | 2,5 | 2,3 | 2,7 | 2,3 | |
| 0,15 | 0,125 | 0,2 | 0,175 | 0,1 | 2,2 | 2,1 | 2,2 | 2,6 | 2,1 | |
| 2,1 | 2,0 | 2,1 | 2,2 | 2,0 |
МЕТОДЫПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА
3.1 Методические указания к первому занятию
При проведении экспериментальных исследований могут решаться две основные задачи:
1. Выявление количественных закономерностей, устанавливающих отношение между переменными, которые описывают объект исследования.
2. Нахождение значений переменных, обеспечивающих оптимальный (по определенному критерию) режим функционирования объекта.
Планирование эксперимента состоит в выборе числа и условий проведения опытов, позволяющих получить необходимые знания об объекте исследов