Описание лабораторного оборудования

ИЗУЧЕНИЕ ЛАЗЕРНОГО УСТРОЙСТВА,

ОБЕСПЕЧИВАЮЩЕГО РЕГИСТРАЦИЮ РАЗГОВОРОВ,

ВЕДУЩИХСЯ В ПОМЕЩЕНИЯХ

Введение

 

Разработано лазерное устройство, обеспечивающее эффективное обна­ружение, подслушивание и регистрацию (перехват) разговоров, ведущихся в помещениях. Дальность действия устройства - 1000м. Устройство сконстру­ировано на основе гелий-неонового лазера, генерирующего электромагнит­ные колебания с длиной волны 632,8 нм (1000нм=1мкм). Прослушивание и перехват переговоров ведутся благодаря получению отраженного сигнала от обычного оконного стекла, представляющего собой своеобразную мембрану, которая колеблется со звуковой частотой, создавая фонограмму происходя­щего разговора.

В целях упрощения эксплуатации и обслуживания устройства приемник и передатчик выполнены раздельно. Кассетное устройство магнитной записи переговоров и специальный блок компенсации помех устанавлива­ются на телескопических треногах, предусмотренных в комплекте устрой­ства. Вся разведывательная аппаратура размещена в небольшом чемодан­чике. Электропитание от батареи.

Цель работы

 

Целью работы является изучение работы лазера, изучение эффекта пе­редачи речевой информации с помощью отраженного от поверхности окон­ного стекла лазерного излучения, а также изучение возможности противо­действия съему такой информации с помощью звукопоглощающих материа­лов и конструкций.

 

Теоретическая часть

Лазерная разведка является одним из перспективных видов РЭР.

Лазеры были созданы в оптическом диапазоне электромагнитных волн, в который входят инфракрасные (0,75 - 1000 мкм), видимые (0,4 - 0,75 мкм) и ультрафиолетовые (0,1 - 0,4 мкм) волны. Еще в начале века было установ­лено, что в оптическом диапазоне волн мельчайшие частицы материи - моле­кулы и атомы - благодаря сложным процессам, происходящим в них, излу­чают электромагнитные волны и являются носителями энергии. Задача за­ключалась в том, чтобы найти способы управления и накопления электро­магнитной энергии, излучаемой атомами и молекулами, имея в виду, что это излучение может происходить не непрерывно, а квантами и в широком опти­ческом диапазоне частот.

Советские ученые Н. Г. Басов и А. М. Прохоров впервые решили про­блему индуцированного излучения в 1952 году, за что им и американскому ученому Ч.Таунсу была присуждена Нобелевская премия (1964 г.). Это от­крытие явилось началом в создании приборов, генерирующих инфракрасные, видимые и ультрафиолетовые лучи.

Приборы, работающие по новому принципу и генерирующие особые по свойствам лучи, были названы квантово-механическими генераторами оптического диапазона волн. Их называют также оптическими квантовыми генераторами, сокращенно - лазерами.

Рассмотрим работу гелий-неонового лазера непрерывного действия. Гелий-неоновые лазеры излучают монохроматический пучок мощно­стью до нескольких десятков милливатт, работают и в импульсном, и в не­прерывном режимах, прочны и сравнительно безопасны в эксплуатации. Эти лазеры генерируют излучение и в видимой, и в инфракрасной областях спек­тра. В видимой области спектра длина волны их излучения приходится на красную часть спектра ( =632,8 нм), в инфракрасной области спектра они генерируют излучение на длинах волн 1150 и 3390 нм. Приборы такого типа стали наиболее распространенным видом лазера.

Принципиальная схема гелий-неонового лазера изображена на рисунке Здесь 1 - газоразрядная стеклянная трубка диаметром несколько миллиметров и длиной от нескольких десятков сантиметров до 1,5 метра и более. Торцы трубки замкнуты плоскопараллельными пластинками, ориен­тированными под углом Брюстера к оси трубки. Для излучения, распростра­няющегося вдоль оси трубки, поляризованного в плоскости падения света на пластинки, коэффициент отражения от них равен нулю.

Рисунок 1

 

Давление гелия в трубке примерно равно 1 мм рт.ст., давление неона -0,1 мм рт.ст. Трубка имеет катод 2, накаливаемый низковольтным источни­ком питания, и цилиндрический пустотелый анод 3. Между катодом и ано­дом на трубку подается напряжение 1-2,5 кВ. Разрядный ток в ней равен не­скольким десяткам миллиампер. Разрядная трубка гелии - неонового лазера помещается между зеркалами 4 и 5.

Зеркала, обычно сферические, делаются с многослойными диэлектри­ческими покрытиями, имеющими высокие значения коэффициента отраже­ния и почти не обладающими поглощением света.

При нагретом катоде трубки и включенном анодном напряжении труб­ка светится и в ней отчетливо виден газоразрядный столб розового цвета. По внешнему виду включенная трубка вполне аналогична газоразрядным неоновым рекламным трубкам. Если через спектроскоп наблюдать ненаправленное свечение этой трубки, то отчетливо видна совокупность многих спектраль­ных линий неона, расположенных в различных областях видимого спектра, и желтые линии свечения гелия. При правильной ориентации через оба зеркала (но в особенности через зеркало с большим значением коэффициента про­пускания) распространяются хорошо коллимированные интенсивные пучки монохроматического (красного) света с длиной волны 632,8 нм. Эти пучки возникают в результате генерации излучения гелий-неонового лазера.

Кратко рассмотрим процессы, которые обеспечивают инверсную засе­ленность уровней неона.

На рисунке 2 приведена упрощенная схема уровней энергии атома неона (справа). Излучению с длинами волн 632,8 нм и 1150 нм соответствуют переходы и . Помимо уровней Е₄, Е₃, Е₂, Е₁, атом неона имеет еще 28 состояний с энергиями меньше, чем E₃ но они для нас несуществен­ны.

Рисунок 2- Энергетические уровни атомов гелия и неона

 

В результате столкновений с электронами газоразрядной плазмы часть атомов возбуждается, что отмечено на рисунке 1.2 вертикальными пунктир­ными стрелками. При определенных режимах разряда этот процесс оказыва­ется достаточным для образования инверсной заселенности уровней Е₂ и Е₁. Однако уровни Е₃, Е₁ и Е3, Е4 переходы между которыми отвечают =632,8 и =3390 нм, заселены не инверсно. Положение изменяется, если в разрядную трубку ввести гелий. Гелий обладает двумя долгоживущими (метастабильными) состояниями E₂, Е₃, по­казанными на левой части; эти состояния возбуждаются при столкновениях с электронами, и ввиду большой длительности их существования концентра­ция метастабильных атомов гелия в разряде очень велика. Энергия E₃, Е₂ метастабильных состояний гелия очень близка к энергиям E₃, Е₂ неона, что благоприятно для передачи энергии возбуждения от гелия к неону при их столкновениях. Эти процессы показаны горизонтальными стрелками.

В результате концентрация атомов неона, находящихся на уровнях E₃, Е₂, резко увеличивается, и возникает инверсная заселенность уровней Е₃ и Е₁, а разность заселенностей уровней Е₁ и Е₂ увеличивается в несколько раз. Таким образом, добавление гелия к неону (примерно в пропорции 5:1-10:1) весьма существенно для генерации в гелий-неоновом лазере. Точные количе­ственные исследования показали, что степень пространственной когерентно­сти 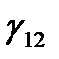излучения гелий-неонового лазера почти равна единице. Например, некогерентная часть потока оказалась порядка для тех точек попе­речного сечения пучка, где интенсивность составляет 0,1% от максимальной, а для точек на оси порядка . Благодаря высокой когерентности гелий-неоновый лазер служит превосходным источником непрерывного монохроматического излучения для исследования всякого рода интерференции и интерференционных явлений. Многочисленные варианты гелий-неонового лазера нашли применение в системах лазерной связи, голографии, в акустоскопии и многих других областях техники.

При использовании лазерного излучения для прослушивания разгово­ров, ведущихся в помещениях, лазерный пучок используется для сканирова­ния (в режиме отражения) поверхности стекла, участки которой испытывают микроперемещения, сопровождающиеся распространением акустической волны.

Опишем простейший случай распространения в помещении плоской монохроматической упругой волны. Амплитуда звукового давления и ско­рость колебаний в этом случае не зависят от расстояния, пройденного волной [2].

Типовое решение волнового уравнения для таких волн, распростра­няющихся в положительном направлении, для скорости колебания

, (1)

где - скорость колебаний частиц воздуха;

U - смещение частиц воздуха под действием звукового давления;

- амплитуда скорости колебаний частиц;

- угловая частота колебаний, ;

f - частота звука;

k - волновое число, ;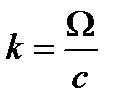

с - скорость распространения звука;

r - радиус-вектор.

Выражение для звукового давления такой волны может быть написано в виде:

 

, (2)

Преломление звуковой волны на границе раздела воздух - стекло при­ведет к тому, что в зависимости от соотношения удельных акустических со­противлений обеих сред часть энергии перейдет из одной среды в другую. Звуковая волна, распространяясь в стекле, может быть описана уравнением движения упругой среды.

Использование закона Р. Гука для изотропного твердого тела (стекла), устанавливающего связь между напряжением () и деформацией , показало, что деформация в упругой плоской волне является функцией одной координаты (например x) и времени [3].

Для анализа распространения упругих волн можно обратиться к общим уравнениям движения упругой среды:

, (3)

где - сила внутренних напряжений среды,

U - ускорение,

р - плотность среды.

Описание плоской монохроматической упругой волны в стекле для вектора смещения такой волны имеет вид:

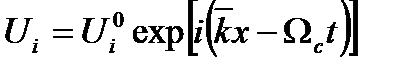, (4)

где - круговая частота.

В [3] подстановкой (4) в (3) для компонент вектора смещения U, были получены следующие выражения:

(5)

где ,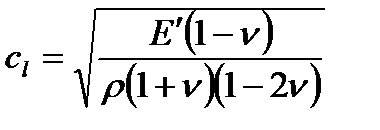

,

Е' - модуль Юнга, ,

S_y - коэффициент упругой податливости,

v - коэффициент Пуассона.

 

Это волновые уравнения в одном измерении, С_l и С_t, - скорости распро­странения волны. Причем из уравнений (5) следует, что скорость распро­странения волны оказывается различной для компонента U₁ и компонентов U₂ и U₃. Таким образом, упругая волна в стекле представляет собой по суще­ству три независимо распространяющиеся в одном направлении волны, в од­ной из которых (U₁) смещение направлено вдоль распространения волны, а в двух других (U₁ и U2) смещение частиц стекла происходит в плоскости, пер­пендикулярной направлению распространения. Первая волна, продольная, распространяется со скоростью с₁, а вторая и третья - поперечные, распро­страняются с одинаковой скоростью с₁, причем с₁ > с_t,

Полученное соотношение справедливо для волн, распространяющихся в среде, неограниченной во всех направлениях.

Поскольку съем информации осуществляется с оконного стекла, по­верхность которого ограничена, толщина стекла мала по сравнению с разме­рами в двух других направлениях, длина акустической волны велика по сравнению с толщиной стекла, за модель следует принять уравнения дефор­мации тонкой пластинки. Сами деформации считаются малыми, критерием малости деформации является малость смещений точек пластины по сравне­нию с ее толщиной.

В [3] получено выражение для полной свободной энергии (F_пл) дефор­мированной пластинки в виде:

(6)

где h - толщина пластинки;

- смещение точек по поверхности вдоль координаты Z, деформация.

Выражение (6) получено из условия, что плоскость х, у совпадает с плоскостью недеформированной пластинки, компоненты смещения точек в плоскости х, у являются величинами второго порядка малости по сравнению с и могут быть положены равными нулю. Вектор смещения точек ней­тральной поверхности:

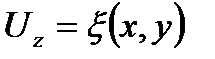, , (7)

Нас интересует форма, принимаемая пластинкой под влиянием прило­женных сил, величина является смещением точек пластинки, рассматри­ваемой как поверхность при ее изгибании.

Уравнение равновесия пластинки, изгибаемой действующими на нее внешними силами [3]:

, (8)

где Р - внешняя сила, отнесенная к единице площади поверхности пластинки и направленная по нормали к ней;

- двухмерный оператор Лапласа;

D - жесткость пластинки.

, (9)

Граничные и краевые условия для уравнения (8) весьма сложны. Для случая, когда пластинка имеет круглую форму и края ее заделаны, эти усло­вия значительно упрощаются, и в [3] определена деформация:

, (10)

где f - приложенная сила;

R - радиус пластинки.

Так, для R = 0,15 м, h = 0,025 м, r = 0,5 м, давления 0,05 Па получено м. Такая деформация соответствует амплитуде давления нормаль­ного разговора на расстоянии 1 м от пластинки.

Волны, распространяющиеся в тонких пластинках, существенно отли­чаются от волн, распространяющихся в неограниченной среде. В пластинках имеют место волны изгиба, при которых колебания происходят в направле­нии, перпендикулярном плоскости пластинки, и сопровождаются ее изгибом [3]. Причем частота свободных колебаний пластинки пропорциональна квадрату волнового вектора, скорость распространения волн изгиба по пла­стинке пропорциональна волновому вектору, а не постоянна, как для волн в неограниченной трехмерной среде: , (11)

где с - групповая скорость в изотропной среде, совпадающая с направлением волнового вектора.

Частота волн изгиба пластинки соответствует частоте вынуждающей силы, т.е. плоская монохроматическая волна акустического поля помещения вызывает периодические, с частотой , упругие деформации по­верхности стекла. Из-за микродеформаций поверхности изменяется с часто­той звука угол падения (и отражения) сканирующего лазерного пучка.

Возможно предположить, что отраженный лазерный пучок из-за пе­риодических изменений угла отражения, попадая на вход фотоумножителя, то в большей, то в меньшей степени перекрывает площадь входного окна фотоумножителя, тем самым изменяя падающий на фотокатод входной поток света, который далее преобразуется в развертку электронного луча.

Установка перед фотоумножителем объектива позволяет сфокусиро­вать отраженный лазерный пучок таким образом, что размер пятна на входе фотоумножителя становится в несколько (~ в 5...6) раз меньше площади его входного окна. С изменением звукового сигнала пятно не смещается на ней. Однако и в этом случае на экране осциллографа фиксируется информация о звуке, переданная отраженным лазерным пучком.

Определим, изменение каких параметров отраженного лазерного излу­чения может передавать информацию об акустическом поле.

Опыты Винера и Айвса [4], связанные с фотографическим действием и фотоэлектрическим эффектом, показали, что они связаны с электрическим вектором электромагнитной волны. Если исходить из электронных представлений, то это легко понять: большинство процессов, наблюдаемых в веществе под действием света, связаны с его воздействием на электроны. Так, при фотоэффекте происходит вырывание электронов из освещаемого металла. Так как электроны представляют собой электрические заряды, то сила, дей­ствующая на них, определяется, в первую очередь, электрическим полем, т.е. электрическим вектором электромагнитной волны, а действие магнитного вектора непосредственно не сказывается [4].

Из вышесказанного вытекает следующая вероятная последователь­ность преобразований информации о звуковом поле [5]:

где - угол падения (отражения) лазерного пучка;

- вектор напряженности электрического поля отраженного пучка;

- круговая частота лазерного излучения;

- интенсивность отраженного пучка;

- переменное напряжение звуковой частоты;

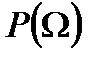- звуковое давление на выходе динамика.

Известно, что излучение лазера является поляризованным. В общем случае эта поляризация эллиптическая. В отличие от геометрических зако­нов, амплитуды отраженной и преломленной волн зависят от поляризации падающей волны. Законы, определяющие направление распространения волн, одни и те же при любой поляризации.

Запишем известные выражения для падающей, отраженной и прелом­ленной волн:

(12)

где С - скорость свет;

, U_j - частоты и скорости волн;

Е_j - амплитуды волн;

n₁, n₂ - показатели преломления граничных сред;

S_j - единичные векто­ры, лежащие в плоскости падения (нормаль к плоскости раздела сред), .

Известны формулы Френеля [4], дающие соотношения между ампли­тудами падающей, отраженной и преломленной волн вектора напряженности электрического поля. Они получены исходя из разложения амплитуд на ком­поненты и , лежащие соответственно в плоскости падения и перпенди­кулярной к ней плоскости отражения:

. (13)

Формулы Френеля позволяют решить задачу отражения и преломления света произвольной поляризации.

(14, 15)

где - угол падения и отражения; - угол преломления.

Поскольку амплитуда вектора напряженности электрического поля па­дающего пучка Е_i не изменяется, а углы и в акустическом поле помещения зависят от , коэффициент Френеля R также будет зависеть от . Сле­довательно, вектор напряженности электрического поля отраженного пучка может быть записан в виде:

. (16)

Изменение амплитуды вектора во времени означает вариацию интен­сивности пучка. Энергия света для отраженной волны, покидающая единицу площади поверхности в единицу времени, выразится соотношением:

. (17)

Из выражения (17) следует, что изменение интенсивности отражен­ного лазерного пучка за счет изменения амплитуды несет информацию об акустическом поле помещения.

Работа фотоумножителя связана с его реакцией на изменение входного потока света. Причем [4]

. (18)

где dФ - изменение светового потока; - площадь окна фотоумножите­ля; - угол между нормалью к плоскости окна и направлением потока; - изменение телесного угла.

Из формулы (18) следует, что изменение потока связано как с изме­нением интенсивности из-за вариации Е_r, так и с изменением диаграммы на­правленности из-за изменения . Расчеты показали, что эти компоненты представляют собой величины одного порядка, сравнимы по абсолютной ве­личине между собой [5].

Таким образом, для создания противодействия такому съему информа­ции необходимо разрабатывать методы, позволяющие уменьшить до нуля R путем создания на стекле специального слоя покрытия.

Для создания препятствия для прослушивания разговоров, ведущихся в помещении, с помощью лазерного излучения возможно использование зву­копоглощающих материалов и конструкций перед оконным стеклом в поме­щении.

Коэффициенты поглощения материалов зависят от частоты. Одни ма­териалы имеют большее поглощение на низких, другие - на высоких, третьи - на средних частотах. Ряд материалов имеет немонотонную зависимость ко­эффициента поглощения от частоты. Все это позволяет подбирать общее по­глощение в помещении оптимальной величины во всем диапазоне частот. Для предотвращения прослушивания в качестве звукопоглощающего материала перед окном можно использовать пористые поглощающие мате­риалы. На рисунке 3 приведены частотные характеристики коэффициентов поглощения пористых материалов: 1 - драпировка на окне, 2 - драпировка на расстоянии 10 см от окна.

Коэффициентом поглощения материала а называется отношение по­глощенной энергии звуковой волны I к падающей энергии I_пад на поверхно­сти этого материала:

.

Для поглощающего материала с размером, сравнимым с длинной зву­ковой волны, коэффициент поглощения зависит от соотношения между ни­ми. Коэффициент поглощения портьеры с небольшими размерами по сравне­нию с длиной звуковой волны больше, чем портьеры с большими размерами. Поэтому лучшее звукопоглощение в помещении обеспечивается, если иметь ряд узких портьер, чем одну широкую (при равной общей ширине).

Из графиков видно, что пористые звукопоглощающие материалы дают преимущественное поглощение в области высоких частот (>1000 Гц) и очень неэффективны в нижней части частотного диапазона.

Рисунок 3 - Частотные характеристики коэффициента поглощения пористых материалов

 

В данном случае может быть использована такая конструкция погло­щающего материала как резонансные поглотители, одним из видов которых является мембранный поглотитель - натянутый холст, прикрывающий окно. Максимум поглощения получается на резонансных частотах. Для натянутого холста с силой P резонансные частоты;

,

где р - плотность материала холста;

l, b, t - длина, ширина и толщина полотна;

k - порядок резонансной частоты.

 

 

Описание лабораторного оборудования

Лабораторная установка для изучения физического эффекта передачи с помощью лазерного пучка информации о звуковой частоте и для изучения влияния звукопоглощающих материалов приведена на рисунке 1.4.

Рисунок 4

 

Установка содержит:

Гелий-неоновый лазер, закрепленный на оптической скамье;

Рейтер с закрепленной в нем стеклянной пластинкой;

Рейтер с закрепленным динамиком, подключенным к генератору звуковой частоты;

Фотоумножитель;

Блок питания лазера;

Источник постоянного тока для питания фотоумножителя;

Осциллограф;

Усилитель;

Динамик;

Генератор низкочастотный ГЗ.

 

Меры безопасности

Подключение к сети источников тока и напряжения осуществляет преподаватель.