Приложение к блоку «Декодер»(ДК) 4 глава

- символ «0» передается импульсом отрицательной полярности. Параметр (или ) может принимать любые значения, например, .

 

 

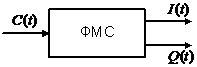
Рис. 1 Формирователь модулирующих символов (ФМС).

Блок ФМС имеет два выхода, на которых формируются выходные

сигналы и .

Фрагмент возможной реализации 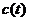случайного процесса , соответствующий заданной последовательности двоичных (бинарных) информационных символов - 1 0 1 1 0, поступающих с выхода кодера (К) представлен на рис. 2б.

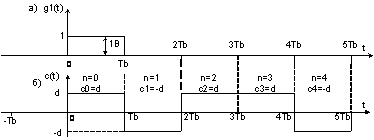
Рис. 2 Импульс и фрагмент реализации .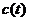

Реализацию 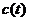случайного процесса

(1)

можно представить в следующей аналитической форме

(2),

где - прямоугольный импульс длительностью (рис. 2а),

при (3).

- прямоугольный импульс такой же формы, как , но сдвинутый вправо относительно импульса на величину , если или влево, если ;

- численный коэффициент, являющийся реализацией случайной величины 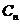на - интервале .

Величина 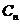принимает два дискретных значения и с вероятностью 0,5 каждое, то есть .

Если в заданной реализации 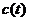на - интервале передается информационный символ «1», то 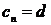, если передается символ «0», то (рис. 2б).

Параметр является величиной безразмерной, принимающей заданное численное значение.

Связь между входным и выходными сигналами блока ФМС характеризует сигнальное созвездие для заданного вида модуляции. Сигнальное созвездие строится в декартовой системе координат и . Каждой точке (звезде) сигнального созвездия будут соответствовать численные значения координат и . Существуют разные формы сигнальных созвездий, но наибольшее практическое применение получили созвездия квадратной формы. Примером таких созвездий являются КАМ-16, КАМ-64, КФМ-4 и другие, где цифры 16, 64 и 4 показывают количество точек в созвездии.

Аббревиатура КАМ и КФМ, соответственно, означает - «квадратурная» амплитудная модуляция и «квадратурная» фазовая модуляция *).

Слово «квадратурная» показывает, что в состав сигнала КАМ или КФМ входит сумма двух сигналов, один из которых зависит от множителя 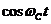, а другой от множителя . Благодаря этим множителям сигналы обладают свойством взаимной ортогональности. Про такие сигналы говорят, что они находятся в «квадратуре».

Количество точек на квадратном созвездии можно представить в виде , где =2,4,6,8, - четное число, то есть задать возможные - битовые блоки или символы. На каждой координатной оси и точкам сигнального созвездия соответствует возможных амплитуд дискретных координатных значений (уровней), которые определяются для каждого значения из выражения

(4),

где возможное количество бит в - битовом блоке (символе).

--------------------------------------------------------------------------------------------

*) В иностранной литературе виды модуляции КАМ-16, КАМ-64, КФМ4 соответственно, обозначают:

QAM - Quadrature Amplitude Modulation,

QPSK – Quadrature Phase Shift Keying.

 

Расстояние между соседними дискретными значениями равно , где

- заданная величина (в частности может быть ). Каждой точке сигнального созвездия соответствует блок из двоичных ИС, которые поступают на вход блока ФМС.

 

Примеры:

1. В случае квадратурной амплитудной модуляции КАМ-16

формируются 16 битовых блоков, каждый из которых несет информацию о четырех битах (квадбите) исходной двоичной последовательности.

Число точек в созвездии равное 16 представляем в виде , где .

Определяем число бит в символе . Используя формулу (4), находим значения (уровни) координат точек созвездия на осях и

-3 , - , , 3 (5).

Итак, сигнальное созвездие для КАМ-16 содержит 16 точек. Существует 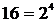различных блоков (последовательностей) из 4-х двоичных символов, отличающихся друг от друга хотя бы одним символом (битом). Отсюда следует, что каждую точку на сигнальном созвездии можно связать с одним из 16-ти символьных блоков. Соответствие между 16 различными блоками из 4-х символов (битов) и 16 точками сигнального созвездия можно осуществлять различными способами.

Наиболее рациональное соответствие получается при использовании

так называемого кода Грея, когда соседним точкам на сигнальном созвездии соответствуют блоки, отличающиеся друг от друга только одним

символом (битом). Приведено сигнальное созвездие для КАМ-16 (рис. 3).

 

Рис. 3 Сигнальное созвездие для КАМ-16.

Действительно, если при передаче сигнала с параметрами и , являющимися координатами какой-либо точки сигнального созвездия, демодулятор, в условиях действия флуктуационной помехи (белого шума),

неверно определит величины передаваемых параметров и , то наиболее вероятные ошибки будут соответствовать координатам и тех точек сигнального созвездия, которые находятся на наименьшем евклидовом расстоянии от точки сигнального созвездия с координатами и .

В этом случае при обратном переходе от принятых параметров и к возможным блокам из 4-х двоичных символов, ошибка будет только в одном символе (бите) из 4-х передаваемых, что важно при декодировании с исправлением ошибок.

Графики на рис. 4 иллюстрируют пример, когда по заданной реализации 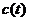входного случайного процесса с использованием сигнального созвездия КАМ-16 строятся реализации и 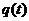выходных случайных процессов и . Процессы и можно представить в виде

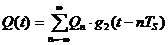; (6),

где - прямоугольный импульс длительностью (рис. 4б);

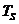- символьный интервал, бинарный интервал.

при (7).

- прямоугольный импульс такой же формы как импульс , но сдвинутый вправо относительно импульса на величину , если или влево, если ;

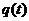Рис. 4 Реализации и случайных процессов и для КАМ-16.

и - независимые случайные величины, заданные на символьном интервале с номером , которые согласно сигнальному созвездию (рис. 3) принимают четыре дискретных значения , , , 3 с вероятностью 0,25 каждое, то есть

(8).

На рис. 4а изображен фрагмент возможной реализации ,

поступающей на вход блока ФМС, соответствующий последовательности двоичных ИС – 1011001001110110. Реализации и 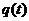в соответствии с выражением (6) можно представить в форме

, (9),

где и - реализации случайных величин и на символьном интервале с номером (рис. 4в,г), входящих в (6).

Пользуясь сигнальным созвездием (рис. 3) для входной реализации 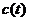(рис. 4а) по 4-м символьным блокам двоичных символов определяются численные значения и на символьном интервале длительностью 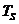с номером , где , , , .

Первые четыре символа (биты) 1 0 1 1 из заданной последовательности 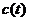расположены над символьным интервалом 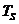с номером . На сигнальном созвездии находим точку, которой соответствует блок из четырех бит 1 0 1 1. Значения реализаций и случайных величин и 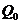будут равны значениям координат найденной точки, то есть и .

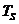Аналогично находим численные значения реализаций и для интервалов с номерами

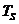Отметим, что сигналы и на рис. 4в и рис. 4г должны быть сдвинуты по оси времени вправо на величину относительно сигнала 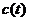на рис. 4а. Чтобы было легче проследить за соответствием между графиком сигнала 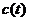и графиками реализаций и , графики рис. 4в и рис. 4г выполнены без указанного сдвига.

2. Сигнальное созвездие КФМ-4 представлено на рис. 5.

 

Рис. 5 Сигнальное созвездие квадратурной фазовой модуляции КФМ-4.

Формально этот вид модуляции можно обозначить как КАМ-4. Поскольку точки (звезды) созвездия (рис. 5) находятся на одинаковом расстоянии от начала координат, то колебания, соответствующие этим точкам, будут иметь одинаковые амплитуды, но разные фазы. Так как сигналы, соответствующие разным точкам созвездия (рис. 5) различаются только фазами, правильнее такие сигналы назвать сигналами «квадратурной» фазовой модуляции КФМ-4. Четырехфазная КФМ-4 основана на передаче четырех сигналов, каждый из которых содержит информацию о двух битах (дибите) исходной двоичной последовательности (00,01,10,11). Соответственно, фаза сигнала может принимать значения (возможно ).

На выходах блока ФМС для КФМ-4 также появляются сигналы и , представленные в виде формул (6),

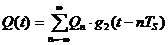; (10),

где и - независимые случайные величины согласно сигнальному созвездию (рис. 5), которые принимают два дискретных значения , и , с вероятностью 0,5 каждое

(11),

где - прямоугольный импульс длительностью с амплитудой (рис. 6б).

- прямоугольный импульс такой же формы, как импульс , но сдвинутый относительно импульса на величину ;

Фрагменты реализаций и случайных процессов и , соответствующие заданной реализации 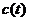входного процесса , представлены на рис. 6.

Рис. 6 Реализации и случайных процессов и для КФМ.

Методика изображения реализаций для КФМ полностью соответствует методике построения реализаций и на рис. 4.

Нетрудно показать, что полученные аналитические выражения (15), (22) для корреляционных функций , являются частными случаями более общего аналитического выражения (26) при соответствующем задании процесса .

Если в качестве случайного процесса выбрать случайные процессы или , задаваемыми, соответственно, в «П4 ФМС формулами (1) и (6)», тогда получим для корреляционных функций этих процессов, соответственно, формулы (15) или (22).

В «П6 к блоку Демодулятор» дается обоснование структурной схемы демодулятора для КАМ-16. Учитывая, что КФМ-4 является КАМ-4, разобраться в материале для КАМ-16 и самостоятельно составить структурную схему демодулятора для КФМ-4.

 

 

«П5 - Модулятор - перемножители, инвертор и сумматор»

 

На структурной схеме системы связи сигнал c выхода

нижнего перемножителя ПМ2 поступает на вход инвертора, который изменяет знак перед этим сигналом с плюса на минус. С учетом этого на выходе сумматора получаем сигнал

(1)

Этот сигнал в зависимости от заданного вида модуляции является сигналом квадратурной амплитудной или квадратурной фазовой модуляции. Множител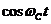и и обеспечивают ортогональность сигналов и . Поэтому говорят, что эти сигналы находятся в квадратуре.

Сигналы, входящие в (1) передаются одновременно, в одной и той же полосе частот и по одной линии связи. Свойство ортогональности

обеспечивает линейную независимость этих сигналов, а значит и возможность их разделения на приемном конце канала. Возможность резделения этих сигналов позволяет независимо производить оценку информационных параметров (модулирующих символов) и в составе сигналов и .

Используя полученные ранее выражения (6) из «П4 к блоку ФМС» для сигналов и , формулу (1) запишем в виде

(2)

Выделим из правой части (2) сигнал 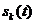, которому соответствует

слагаемое с индексом 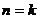, где - произвольное фиксированное целое

число =

(3).

С помощью сигнала (3) по каналу передаются информационные (модулирующие) символы 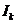и 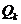. Сигнал (3) появляется на выходе модулятора, начиная с момента и его длительность равна длительности импульса .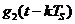

Из «П4 блока ФМС» следует, что символы 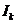и 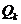являются декартовыми координатами точки 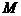на сигнальном созвездии (рис. 1), которая соответствует выделенным слагаемым из выражения (2).

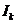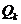Рис. 1 Координаты и точки 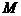на сигнальном созвездии.