Приложение к блоку «Декодер»(ДК) 7 глава

Имея в виду на интервале интегрирования, и , тогда .

Используя (17), получим .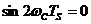

Окончательно, имеем

(27).

Подставляя (27) в (26), получим

; ; (28).

Если одновременно будут выполняться все три неравенства (28), то РУ1 вынесет правильное решение о том, что в соответствии с (19) значение ИС будет равно .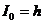

Если хотя бы одно из неравенств (28) выполняться не будет, тогда демодулятор примет ошибочное решение. На рис. 4 штриховкой обозначены те области на оси , на которых выполняются соответствующие неравенства из системы (28).

 

Рис. 4 Интервал , на котором одновременно выполняются неравенства (28).

На рис. 4 определяем, что случайная величина будет удовлетворять неравенству

(29),

если одновременно выполняются три неравенства из (28).

Отсюда следует, что вероятность выполнения неравенства (29) равна вероятности правильного решения , которое принимает РУ1 при передаче значения ИС равного 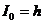. Вероятность невыполнения неравенства (29) равна вероятности ошибочного решения . Чтобы найти численные значения и , необходимо определить плотность вероятности , которая характеризует случайную величину равной выражению (23). Интегралу (23) соответствует линейный оператор, воздействующий на гауссовский случайный процесс 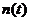в составе подынтегральной функции. Известно, что воздействие любого линейного оператора на гауссовский процесс сохраняет гауссовское свойство, то есть - гауссовская случайная величина. Поскольку - гауссовская плотность вероятности, то ее характеризуют два параметра – математическое ожидание и дисперсия . Определим эти параметры

(30), Так как математическое ожидание белого шума , а - центрированная случайная величина, поэтому ее дисперсия определяется

. Делаем замену правой частью (23). Получим

, где - корреляционная функция белого шума 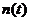, то есть ;

- заданная односторонняя спектральная плотность мощности белого шума; 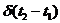- дельта функция.

Таким образом, .

Используя фильтрующее свойство 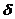- функции, а также (17) и , получим . Используя (27) будем иметь

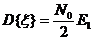(31).

Одномерную плотность вероятности (рис. 5), имея в виду (30) и (31), можно представить в виде

(32).

 

Рис. 5 График , где заштрихованная площадь

есть вероятность правильного решения при значении .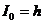

Вероятность правильного решения

= (33),

есть вероятность выполнения неравенства (29) и равна величине заштрихованной площади (рис. 5).

Используя (32), получим = = .

Произведем замену на переменную интегрирования по формуле

, откуда , при , а при .

В результате получим интеграл

(34).

В математических справочниках [6] можно найти специальную функцию, которая называется «интегралом вероятности» или функцией Крампа, ее аргументом является верхний предел интеграла

(35), Эта функция табулирована. Сравним (34) и (35), получим

(36)

Используя (31) можно написать

(37).

Вероятность ошибочного решения, принимаемого РУ1 будет равна

(38).

2. Пусть значения переданных информационных символов (ИС) равны

; (39).

Повторяя по аналогии выкладки, рассмотренные в случае 1, получим следующие напряжения на соответствующих входах РУ1 в момент окончания символьного интервала длительностью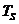

На 1-м входе ; на 2-м входе ;

на 3-м входе ; на 4-м входе (40),

Значение означает, что теперь в составе информационной части входного сигнала 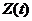содержится сигнал из (6). Поэтому при правильном решении, принимаемым РУ1, наибольшее напряжение будет на его третьем входе, то есть должны одновременно выполняться три неравенства

> ; > ;

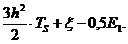> .Три неравенства после элементарных преобразований, с учетом (27) примут вид

; ; (41).

Три неравенства (41) одновременно будут выполняться, если случайная величина удовлетворяет неравенству

(42)

Вероятность правильного решения, принимаемого РУ1, будет равна вероятности выполнения неравенства (42), то есть

, (43)

где определяется из (32).

Рис. 6 Величина заштрихованной площади равна вероятности

правильного решения РУ1 при

При сравнении рис. 5 и рис. 6 видно, что вероятность ошибки при 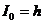равна площади двух незаштрихованных «хвостов», создаваемых кривой , которые, соответственно, уходят в и в . Из рис. 5 видно, что вероятность ошибки при равна площади только одного «хвоста» от до величины . Отсюда следует

(44).

Используя (38), получим из (44)

(45).

Аналогично выше изложенному определяются вероятности ошибок при и , а также вероятности ошибок в работе РУ2.

Вероятности ошибок в работе РУ1 и РУ2, при различных значениях передаваемых ИС и , представлены в таблице 1 и таблице 2.

Таблица 1

Передаваемая величина ИС	Вероятность ошибки в работе РУ1

Таблица 2

Передаваемая величина ИС	Вероятность ошибки в работе РУ2

 

Решения, принимаемые РУ1 и РУ2 о значениях передаваемых символов и в виде соответствующих сигналов, поступают на входы преобразователя параллельного кода в последовательный код.

Ошибки на выходе этого преобразователя происходят в трех случаях:

1. Когда значение передаваемого символа определено ошибочно (будем считать, что произошло случайное событие А).

2. Когда значение передаваемого символа определено ошибочно (будем считать, что произошло случайное событие В).

3. Когда значение обоих передаваемых символов и определены ошибочно.

Из теории вероятности есть известные определения:

Суммой двух случайных событий А и B называется такое третье событие С=А+В, которое состоит в наступлении или события А, или события В, или в наступлении обоих событий А и В. Для обозначения суммы применяется запись С=А+В. При этом вероятность суммы определяется по формуле

Р(С)=Р(А+В)=Р(А)+Р(В)-Р(А*В), (46)

Где через А*В обозначено произведение событий А и В, которое состоит в осуществлении и события А и события В. Вероятность произведении А*В определяется по формуле

Р(А*В)=Р(А)*Р(В/А)=Р(В)*Р(А/В), (47),

где Р(В/А) и Р(А/В) – условные вероятности.

Если события А и В независимы, то

Р(А*В)=Р(А)*Р(В) (48).

И формула(46) примет вид

Р(С)=Р(А+В)=Р(А)+Р(В)-Р(А)*Р(В) (49).

Нетрудно определить вероятность ошибки на выходе преобразователя, когда ошибки на выходах РУ1 и РУ2 происходят независимо. Пусть, например, на -м интервале передаются значения ИС и , тогда, используя (49), можно определить вероятность ошибки на выходе преобразователя

= + - . (50)

В правую часть формулы (50) входят вероятности ошибки на выходах РУ1 и РУ2.

Для четырех точек сигнального созвездия КАМ-16, координаты которых

и могут иметь следующие значения, приведены в таблице 1

и таблице 2.

Таблица 1.

Таблица 2

 

В соответствии с таблицами 1 и 2 вероятности ошибок на выходе преобразователя будут одинаковыми и их величину можно рассчитать по формуле (50).

Для других четырех точек сигнального созвездия, у которых координаты и равны значениям по таблице 2, в соответствии с таблицами 1 и 2 вероятности ошибок на выходе преобразователя также будут одинаковыми и их величину можно рассчитать по формуле, приведенную ниже, вероятности ошибки

= + - . (51)

Для остальных восьми точек сигнального созвездия, координаты равны значениям и по следующей таблице 3

Таблица 3.

 

и вероятности ошибок на выходе преобразователя также будут одинаковыми и их величину можно рассчитать по формуле, приведенную ниже

= + - . (52)

Учитывая, что всего на сигнальном созвездии КАМ-16 содержится 16 точек, среднюю величину вероятности ошибки на выходе преобразователя можно определить

=( + + )/ 16. (53)

 

П7 – к блоку ДЕКОДЕР

Приложение к блоку «Декодер»(ДК)

Рассмотрим выполнение задания по блоку «Декодер» на конкретном примере. Пусть m – номер варианта курсовой работы равен m=71.

1)В соответствии с таблицей (полученной для этого варианта) выписываем из 2-й строки численные значения принятых кодовых символов, которые образуют последовательность

(Крестиком отмечен кодовый символ, который был принят ошибочно).

2)Строим решетчатую диаграмму декодера с учетом полученной последовательности