Напомним, что в блоке АЦП передающего устройства точному отсчету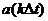 
аналогового сигнала 
в момент времени 
сопоставляется ближайший номер уровня квантования в виде целого положительного числа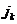 
. Величине 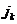соответствует последовательность определенного числа двоичных информационных символов (ИС), передаваемых по каналу связи. Предполагается, что возможные ошибки, которые могли произойти на выходе демодулятора, исправлены в декодере и на вход ЦАП поступает цифровой сигнал ИС, соответствующий уровню квантования .
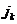В момент времени в ЦАП генерируется прямоугольный импульс длительностью 
с амплитудой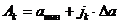 
, где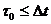 
.
Изображена последовательность таких прямоугольных импульсов в зависимости от длительности , начиная с момента времени 
на рис. 1а,б.
Рис. 1 Последовательность прямоугольных импульсов в ЦАП пр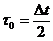и 
и 
.
Последовательность прямоугольных импульсов (рис. 1) поступает на вход ФНЧ, входящего в цифроаналоговый преобразователь (ЦАП). На выходе ФНЧ формируется аналоговый сигнал 
, изображенный в виде сплошной жирной кривой на рис. 1а, б. С достаточной для практики и степенью точности сигнал 
должен воспроизводить исходный аналоговый сигнал , который по структурной схеме поступает с выхода источника сообщений на вход АЦП. Разностный сигнал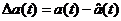 
или шаг квантования является погрешностью (ошибкой) квантования, так как не превышает половины шага квантования и называют шумом квантования.
Во-первых, теоретически погрешность 
возникает в результате того, что точные отсчеты 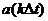аналогового сигнала , получаемые в АЦП, меняются на значения ближайших уровней квантования 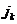. Шум квантования не связан с помехами в канале и определяется выбором числа уровней квантования. Его можно сделать сколь угодно малым, если увеличивать число уровней. При этом придется увеличивать разрядность, то есть увеличивать число кодовых символов, приходящихся на каждый отсчет.
Следовательно, во-вторых, нужно сокращать длительность символа и расширять спектр сигнала в канале. Таким образом, снижение шума квантования достигается за счет расширения спектра сигнала.
В разделе курса ТЭС «Дискретизация непрерывных сигналов» [ ] отмечалось, что из непрерывного сигнала с финитным спектром можно сформировать новый сигнал 
в виде последовательности
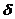- импульсов (рис. 2б).
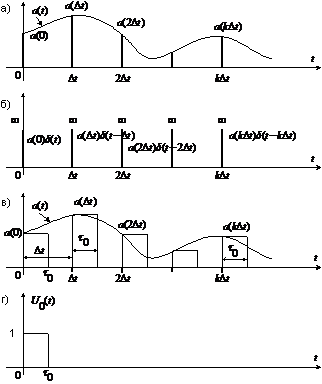
Рис. 2 а) аналоговый сигнал ; б) и в) – возможные импульсные сигналы, сформированные на основе аналогового сигнала .
На рис. 2 изображены следующие величины:
- величины отсчетов - 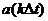сигнала в моменты времени кратные 
, то есть , 
(рис. 2а);
- - интервал дискретизации, удовлетворяющий условию 
, где
- верхняя (наибольшая) частота в спектре сигнала .
Если подать сигнал (рис. 2б) на вход идеального ФНЧ, то на выходе ФНЧ получим сигнал, форма которого в точности соответствует форме исходного аналогового сигнала .
Теперь выясним влияние конечной длительности прямоугольных импульсов (рис. 2в) на величину погрешности .
Обозначив через 
прямоугольный импульс длительностью с амплитудой 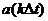на рис. 2в. Этот импульс можно представить в виде свертки прямоугольного импульса 
(рис. 2г) с импульсом (рис. 2б)
(1).
Тогда 
(2). Действительно, подставив (1) в (2)
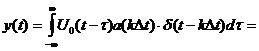
и, используя «фильтрующее свойство 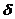- функции *), получим
(3).
Отсюда следует, что форма импульса определяется формой импульса , смещенного по оси времени 
вправо на интервал 
. Амплитуда импульса равна 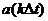, так как согласно рис. 2г амплитуда импульса 
равна единице.
Таким образом, свертка (3) определяет прямоугольный импульс изображенный на рис. 2в. длительностью с амплитудой 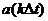. Полученный результат позволяет всю последовательность прямоугольных импульсов (рис. 2в) представить в виде свертки импульса с последовательностью 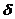- импульсов на рис. 2б, тогда
(4).
Функции соответствует спектральная плотность
(5),
а функции 
соответствует периодическая спектральная
________________________________________________________________
*) «Фильтрующее свойство 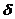- функции » определяется равенством
, где 
- произвольная функция .
плотность с периодом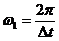 
.
(6),
где 
- финитная спектральная плотность аналогового сигнала (рис. 3а).
Рис. 3
Свертка (4) является функцией аргумента и имеет спектральную плотность 
, равную произведению спектральных плотностей сворачиваемых функций, то есть произведению функций, определяемых равенствами (5) и (6)
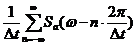(7).
- 
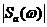- модуль финитной спектральной плотности аналогового сигнала (рис. 3а);
- 
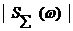- модуль, соответствующий сигналу в виде последовательности 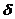- функций (рис. 2б);
- 
- графики модулей спектральной плотности 
прямоугольного импульса для значений и 
, соответственно, для рис. 3в и рис. 3г.
- - график модуля спектральной плотности, определяемой (7), как результат перемножения графиков рис. 3б и рис. 3в.
Аналогично – результат перемножения графиков рис. 3б и рис. 3г.
График модуля передаточной функции идеального ФНЧ с частотой среза 
(рис. 3ж).
График модуля спектральной плотности восстановленного сигнала , который получим на выходе ФНЧ в соответствии с выражением,
как результат перемножения графиков рис. 3д и рис. 3ж, или рис. 3е и рис. 3ж в зависимости от величины длительности .
Рис. 4
Под входным сигналом 
(рис. 4) понимается сигнал в виде последовательности прямоугольных импульсов на рис. 2в.
Учитывая форму графика на рис. 3ж рассмотрим два варианта:
1. Спектральная плотность 
будет равна участку на графике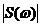 
на рис. 3д между частот 
и 
.
2. Спектральная плотность будет равна участку на графике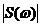
на рис. 3е между частот и .
Рассматривая 1 - й случай, убеждаемся, что спектральная плотность 
будет заметно отличаться от спектральной плотности 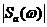на рис. 3а. Делаем вывод, что погрешность восстановления 
исходного аналогового сигнала будет достаточно большой.
Во 2 - м случае спектральная плотность будет меньше
отличаться от спектральной плотности 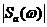на рис. 3а. Делаем вывод, что при уменьшении длительности прямоугольных импульсов на рис. 2в, величина погрешности восстановления уменьшается.
Литература.
1. А.Г.Зюко, Д.Д.Кловский, М.В.Назаров, Л.М.Финк Теория передачи сигналов Изд. 2-е, перераб. и дополнен. М.: «Радио и связь»,1986 304с.: ил.
2. А.Г.Зюко, Д.Д.Кловский, Коржик В.И., М.В.Назаров Теория электрической связи.: Учебник для вузов – М.: Радио и связь, 1998.
3. Скляр Бернард Цифровая связь. Теоретические основы и практическое применение. Изд.2-2, испр.: Пер. с англ. – М.: Издательский дом «Вильямс», 2003.- 1104с.: ил. Парал тит.англ.
4. Дж.Кларк, мл.Дж.Кейн «Кодирование с исправлением ошибок в системах цифровой связи» Пер.с англ. С.И.Гельфонда под ред. Б.С.Цыбакова вып.28 – М.Б»Радио и связь» 1987, 392 с.: ил.
5. Л.Ф. Григоровский, В.И.Коржик, В.Г.Красов, В.Ф.Кушнир «Теория электрической связи. Модели сигналов и методы их преобразования в системах связи»: учеб. Пособие, ЛЭИС. – Л.,1990.
6. В.И.Тихонов «Статистическая радиотехника» Изд. 2-е, перераб. и дополнен. М.: «Радио и связь»,1982 624с.
7. Л.Н Куликов, М.Н Москалец, Теория электрической связи. Основы сверточного кодирования» Учеб. пособие, СПб. – Л., 2006.
Дополнительная литература.
8. Р.Р.Биккенин, М.Н.Чесноков «Теория электрической связи»: учеб. Пособие, ЛЭИС. – Л.,2010.
9. Прокис Дж. Цифровая связь Перевод с англ./ под ред. Д.Д.Кловского, М.: Радио и связь. 2000. – 800 с.: ил.
10. И.Н.Бронштейн, К.А.Семендяев. Справочник по математике для инженеров и учащихся втузов. М. – «Наука»,1964.