Метод Эйлера
Пусть дано дифференциальное уравнение 
(I), с начальными условиями y(
Пусть y=y(x) искомое точное решение. Интегральная кривая проходит через точку (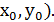
Найдем приближенные значения функции в точках 
. Построим систему равноотстоящих точек узлов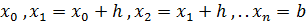 
Проведем прямые 
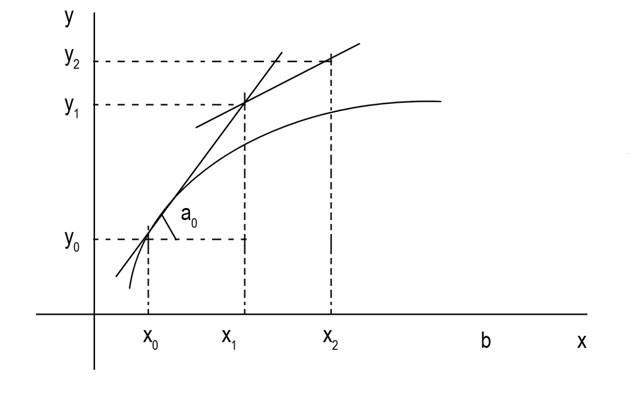
Рассмотрим отрезок [ 
]
На этом отрезке есть одна точка, которая принадлежат искомой кривой - это точка А 
Заменим дугу искомой кривой y=y(x) на отрезке [ ] касательной к ней, проведенной в точке ()
В качестве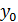 
возьмем ординату точки пересечения прямой x= 
с касательной.
Очевидно 
. Но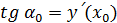 
,
т.е. 
.
Но из уравнения (I) следует, чтo 
Итак, получаем 
.
Предположим теперь, что точка 
принадлежит искомой кривой. В этой точке опять проведем касательную к графику функции до пересечения с прямой х = 
.
Тогда аналогично:
.
Продолжая и так далее, получим систему значений 
которые и будут приближенными значениями функции y=y(x) в точках
Итак, расчетные формулы метода Зилера:
.
Для системы дифференциальных уравнений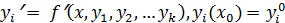 
i= I,…,k
расчетные формулы записываются аналогично
здесь i - номер уравнения в системе, n - номер шага.
Метод Эйлера является грубым методом, ошибка, которую мы допус каем ка каждом шаге пропорциональна 
, т.е. 
.
Чтобы повысить точность вычислений, использует некоторые усовершенствованные методы.
Метод Эйлера-Коши
Пусть опять решаем уравнение y’=f(x,y), y(
Решение ищем на отрезке [ 
].
Пусть нам известны координаты некоторой точки, принадлежащей искомому решению (
). Найдем средний тангенс угла наклона касательной для двух точек: () и (
).
Последняя точка, есть та самая, которую в методе Эйлера мы обозначаем (
), но здесь точка будет вспомогательной.
Итак, сначала по методу Эйлера находится точка А, лежащая на прямой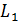 
, тангенс угла наклона которой 
В этой точке снова вычисляется тангенс угла наклона касательной 
Затем через точку () проводим прямую L, тангенс угла наклона которой равен
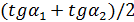
Точка, в которой L пересечется с прямой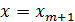 
,будет искомой(). Таким образом, 
есть искомое приближение значения функции на данном шаге интегрирования.
Расчетные формулы метода Эйлера-Коша следующие:
Аналогично, для системы дифференциальных уравнений:
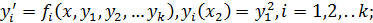
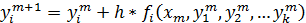
Здесь i - номер уравнения системы, m - номер шага.
Пример.
Задано:
Уравнение у¢×у + 2х2 = 0 на интервале [1,2] при условии у(1) = 3. Представим уравнение в виде у¢ = -2х2/у. Разобьем интервал [1,2] на десять шагов с шагом h = 0,1.
Расчетные формулы метода Эйлера-Коши:
Первый шаг (i = 0):
х1 = х0 + h = 1 + 0,1 = 1,1;
1= y0 + h × f(y0, x0) = 3 + 0,1(-2×12)/3 = 2,93.
х2 = х1 + h = 1,1 + 0,1 = 1,2;
y2 = y1 + (h/2) × (f(y0, x0)+ f( 1, x1)) = 2,93 + (0,1/2)*((-2×1,12)/2,93+(- 2*1,1^2/2.93)) = 2,85633.
Аналогично можно найти значения искомой величины на всём интервале.
Полученные данные позволяют построить график искомой функции на заданном интервале изменения аргумента:
Метод Рунге-Кутта 2-го порядка
Пусть имеем дифференциальное уравнение 
с начальными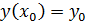 
.
Ищем решение на отрезке [ ].
Пусть имеем точку () принадлежащую искомому решению. Для
того, чтобы найти следующую точку проведем касательную к кривой в точке (
)
До пересечения с прямой 
где 
Тогда, получим координату (по формуле Эйлера)
Теперь найдем тангенс угла наклона касательной в т.В (
(прямая L).
Через точку А про ведем прямую I ||L. Ординату точки пересечения прямых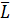 
и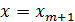
возьмем в качестве 
Таким образом
для системы дифференциальных уравнений
расчетные формулы имеют вид:
Пример.
Задано:
Уравнение у¢×у + 2х2 = 0 на интервале [1,2] при условии у(1) = 3. Представим уравнение в виде у¢ = -2х2/у. Разобьем интервал [1,2] на десять шагов с шагом h = 0,1.
Расчетные формулы метода Рунге-Кутта 2-го порядка:
Пример вычисления (первый шаг):
x0+1/2 = х0 + h/2 = 1 + 0,1/2 = 1,05;
y1+1/2 = y0 + h/2 × f(y0, x0) = 3 + (0,1/2)(-2×12)/3 = 2,9666.
x1 = х0 + h = 1 + 0,1 = 1,1;
y1 = y0 + h × f(y0+1/2, x0+1/2) = 2,96+(0,1)*(-2*1,05^2/2,96)=2,885506.
Аналогично можно найти значения искомой величины на всём интервале.
Полученные данные позволяют построить график искомой функции на заданном интервале изменения аргумента:
ПРОГРАММА МЕТОДА РУНГЕ-КУТТА 2-ГО ПОРЯДКА