Задание
Для курсового проекта по дисциплине
Технология разработки программного обеспечения
Вариант № 11
Темы:
1)Структурное программирование
2)Стиль программирования
3)Надёжность программного обеспечения
4)Тестирование и отладка программ
5)Документирование программ
6)Этапы жизненного цикла программы
Порядок выполнения проекта:
1)Постановка задачи
2)Разработка эскизного проекта
3)Разработка технического проекта
4)Проектирование тестовых примеров
5)Разработка модулей программы
6)Отладка и тестирование программного продукта
7)Разработка программной документации
8)Оформление пояснительной записки и графической части проекта
Условие задачи:
1) Реализовать шифры: сдвига, афинную систему подстановок Цезаря, систему Цезаря с ключевым словом, простую замену. Для передачи ключа использовать одну из ассиметричных криптосистем (Диффи-Хеллмана, RSA, Шамира, Эль-Гамаля)
Пользуясь изложенным способом
1. Зашифровать данный текст;
2. Расшифровать данный текст.
| Содержание
Введение…………………………………………………………………………………….
1.ТЕОРЕТИЧЕСКАЯ ЧАСТЬ………………………………………………………………………
1.1 Что такое криптография…………………………………………………………………
1.2 Передача ключа методом Диффи-Хеллмана…………………………………………..
1.3 Шифр сдвига………………………………………………………………………………
1.4 Шифр «Афинная система подстановок Цезаря»……………………………………….
1.5 Шифр «Система Цезаря с ключевым словом»…………………………………………..
1.6 Шифр простой замены…………………………………………………………………….
2.ПРАКТИЧЕСКИЙ РАЗДЕЛ……………………………………………………………………….
2.1 Расширенная постановка задачи………………………………………………………….
2.2 Эскизный проект…………………………………………………………………………..
2.3 Технический проект алгоритма…………………………………………………………..
3.ИНСТРУКЦИЯ ПОЛЬЗОВАТЕЛЯ………………………………………………………………..
Заключение…………………………………………………………………………………………….
Список использованной литературы…………………………………………………………………
ПРИЛОЖЕНИЕ А Листинг программы……………………………………………………………..
ПРИЛОЖЕНИЕ Б Результат работы программы……………………………………………………
|
| Введение
Разные люди понимают под шифрованием разные вещи. Дети играют в игрушечные шифры и секретные языки. Это, однако, не имеет ничего общего с настоящей криптографией. Настоящая криптография (strongcryptography) должна обеспечивать такой уровень секретности, чтобы можно было надёжно защитить критическую информацию от расшифровки крупными организациями – такими как мафия, транснациональные организации и крупные государства. Настоящая криптография в прошлом использовалась лишь в военных целях. Однако сейчас, со становлением информационного общества, она становится центральным инструментом для обеспечения конфиденциальности. По мере образования информационного общества, крупным государствам становятся доступны технологические средства тотального надзора за миллионами людей. Поэтому криптография становится одним из основных инструментов обеспечивающих конфиденциальность, доверие, авторизацию, электронные платежи, корпоративную безопасность и бесчисленное множество других вещей.
Базовая терминология.
Представьте, что вам надо отправить сообщение адресату. Вы хотите, чтобы никто кроме адресата не мог прочитать отправленную информацию. Однако всегда есть вероятность, что кто-либо вскроет конверт или перехватит электронное послание.
В криптографической терминологии исходное послание именуют открытым текстом. Изменение исходного текста так, чтобы скрыть от прочих его содержание, называют шифрованием. Зашифрованное сообщение называют шифротекстом. Процесс, при котором из шифротекста извлекается открытый текст, называют дешифровкой. Обычно в процессе шифровки и дешифровки используется некий ключ и алгоритм обеспечивает, что дешифрование можно сделать лишь зная этот ключ.
|
| 1.ТЕОРЕТИЧЕСКИЙ РАЗДЕЛ
1.1Что такое криптография?
Криптография (от др.-греч.κρυπτός — скрытый и γράφω — пишу) — наука о методах обеспечения конфиденциальности (невозможности прочтения информации посторонним) и аутентичности (целостности и подлинности авторства, а также невозможности отказа от авторства) информации.
Изначально криптография изучала методы шифрования информации — обратимого преобразования открытого (исходного) текста на основе секретного алгоритма или ключа в шифрованный текст (шифротекст). Традиционная криптография образует раздел симметричных криптосистем, в которых зашифрование и расшифрование проводится с использованием одного и того же секретного ключа. Помимо этого раздела современная криптография включает в себя асимметричные криптосистемы, системы электронной цифровой подписи (ЭЦП), хеш-функции, управление ключами, получение скрытой информации, квантовую криптографию.
Криптография не занимается: защитой от обмана, подкупа или шантажа законных абонентов, кражи ключей и других угроз информации, возникающих в защищенных системах передачи данных.
Криптография — одна из старейших наук, её история насчитывает несколько тысяч лет.
|
| 1.2 Передача ключа методом Диффи-Хеллмана
Протокол Диффи-Хеллмана — криптографический протокол, позволяющий двум и более сторонам получить общий секретный ключ, используя незащищенный от прослушивания канал связи. Полученный ключ используется для шифрования дальнейшего обмена с помощью алгоритмов симметричного шифрования.
Схема открытого распределения ключей, предложенная Диффи и Хеллманом, произвела настоящую революцию в мире шифрования, так как снимала основную проблему классической криптографии — проблему распределения ключей
В чистом виде алгоритм Диффи-Хеллмана уязвим для модификации данных в канале связи, в том числе для атаки «Человек посередине», поэтому схемы с его использованием применяют дополнительные методы односторонней или двусторонней аутентификации.
При работе алгоритма каждая сторона:
1. генерирует случайное натуральное число a — закрытый ключ
2. совместно с удалённой стороной устанавливает открытые параметры p и g (обычно значения p и g генерируются на одной стороне и передаются другой), где
p является случайным простым числом
(p-1)/2 также должно быть случайным простым числом (для повышения безопасности)[7]
g является первообразным корнемпо модулю p
3. вычисляет открытый ключ A, используя преобразование над закрытым ключом
A = ga mod p
4. обменивается открытыми ключами с удалённой стороной
5. вычисляет общий секретный ключ K, используя открытый ключ удаленной стороны B и свой закрытый ключ a
K = Ba mod p
К получается равным с обеих сторон, потому что:
Ba mod p = (gb mod p) a mod p = gab mod p= (ga mod) b mod p = Ab mod p
|
1.3 Шифр сдвига
Шифр Цезаря, также известный как шифр сдвига, код Цезаря или сдвиг Цезаря — один из самых простых и наиболее широко известных методов шифрования.
Шифр Цезаря — это вид шифра подстановки, в котором каждый символ в открытом тексте заменяется символом, находящимся на некотором постоянном числе позиций левее или правее него в алфавите. Например, в шифре со сдвигом вправо на 3, А была бы заменена на Г, Б станет Д, и так далее.
Шифр назван в честь римского императора Гая Юлия Цезаря, использовавшего его для секретной переписки со своими генералами.
Шаг шифрования, выполняемый шифром Цезаря, часто включается как часть более сложных схем, таких как шифр Виженера, и все ещё имеет современное приложение в системе ROT13. Как и все моноалфавитные шифры, шифр Цезаря легко взламывается и не имеет практически никакого применения на практике.
 Рисунок 1- пример шифрования сдвигом
Шифр Цезаря со сдвигом на 3: A заменяется на D B заменяется на E и так далее Z заменяется на С
Если сопоставить каждому символу алфавита его порядковый номер (нумеруя с 0), то шифрование и дешифрование можно выразить формулами модульной арифметики:
Рисунок 1- пример шифрования сдвигом
Шифр Цезаря со сдвигом на 3: A заменяется на D B заменяется на E и так далее Z заменяется на С
Если сопоставить каждому символу алфавита его порядковый номер (нумеруя с 0), то шифрование и дешифрование можно выразить формулами модульной арифметики:
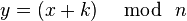
 где
где 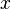 — символ открытого текста, — символ открытого текста, 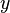 — символ шифрованного текста, — символ шифрованного текста,  — мощность алфавита, а — мощность алфавита, а 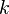 — ключ. — ключ.
|
1.4 Шифр «Афинная система подстановок Цезаря»
Аффинный шифр — это частный случай более общего моноалфавитного шифра подстановки. К шифрам подстановки относятся также шифр Цезаря, ROT13 и Атбаш. Поскольку аффинный шифр легко дешифровать, он обладает слабыми криптографическими свойствами.
В аффинном шифре каждой букве алфавита размера 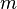 ставится в соответствие число из диапазона ставится в соответствие число из диапазона 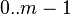 . Затем при помощи модульной арифметики для каждого числа, соответствующего букве исходного алфавита, вычисляется новое число, которое заменит старое в шифротексте. Функция шифрованиядля каждой буквы: . Затем при помощи модульной арифметики для каждого числа, соответствующего букве исходного алфавита, вычисляется новое число, которое заменит старое в шифротексте. Функция шифрованиядля каждой буквы:
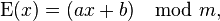 где модуль m– размер алфавита,а пара a иb - ключ шифра. Значение должно быть выбрано таким, что a и m - взаимно простые числа. Функция расшифрования:
где модуль m– размер алфавита,а пара a иb - ключ шифра. Значение должно быть выбрано таким, что a и m - взаимно простые числа. Функция расшифрования:
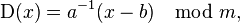 где
где 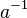 — обратное к aчисло по модулю m.
Примеры шифрования и расшифрования
В следующих примерах используются латинские буквы от A до Z, соответствующие им численные значения приведены в таблице. — обратное к aчисло по модулю m.
Примеры шифрования и расшифрования
В следующих примерах используются латинские буквы от A до Z, соответствующие им численные значения приведены в таблице.
| A
| B
| C
| D
| E
| F
| G
| H
| I
| J
| K
| L
| M
| N
| O
| P
| Q
| R
| S
| T
| U
| V
| W
| X
| Y
| Z
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
Шифрование
В этом примере необходимо зашифровать сообщение "ATTACK AT DAWN", используя упомянутое выше соответствие между буквами и числами, и значения 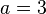 ,
, 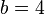 и
и 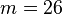 , так как в используемом алфавите 26 букв. Только на число
, так как в используемом алфавите 26 букв. Только на число  наложены ограничения, так как оно должно быть взаимно простым с 26. Значение
наложены ограничения, так как оно должно быть взаимно простым с 26. Значение 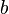 может быть любым, только если
может быть любым, только если  не равно единице, так как это сдвиг шифра.
не равно единице, так как это сдвиг шифра.
Итак, для нашего примера функция шифрования  . Первый шаг шифрования — запись чисел, соответствующих каждой букве сообщения.
. Первый шаг шифрования — запись чисел, соответствующих каждой букве сообщения.
Теперь, для каждого значения 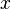 найдем значение
найдем значение  . После нахождения значения
. После нахождения значения  для каждого символа возьмем остаток от деления
для каждого символа возьмем остаток от деления  на 26.
на 26.
Последний шаг процесса шифрования заключается в подстановке вместо каждого числа соответствующей ему буквы.
 Рисунок 1- пример шифрования сдвигом
Шифр Цезаря со сдвигом на 3: A заменяется на D B заменяется на E и так далее Z заменяется на С
Если сопоставить каждому символу алфавита его порядковый номер (нумеруя с 0), то шифрование и дешифрование можно выразить формулами модульной арифметики:
Рисунок 1- пример шифрования сдвигом
Шифр Цезаря со сдвигом на 3: A заменяется на D B заменяется на E и так далее Z заменяется на С
Если сопоставить каждому символу алфавита его порядковый номер (нумеруя с 0), то шифрование и дешифрование можно выразить формулами модульной арифметики:
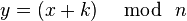
 где
где 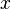 — символ открытого текста,
— символ открытого текста, 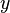 — символ шифрованного текста,
— символ шифрованного текста,  — мощность алфавита, а
— мощность алфавита, а 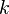 — ключ.
— ключ.
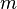 ставится в соответствие число из диапазона
ставится в соответствие число из диапазона 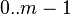 . Затем при помощи модульной арифметики для каждого числа, соответствующего букве исходного алфавита, вычисляется новое число, которое заменит старое в шифротексте. Функция шифрованиядля каждой буквы:
. Затем при помощи модульной арифметики для каждого числа, соответствующего букве исходного алфавита, вычисляется новое число, которое заменит старое в шифротексте. Функция шифрованиядля каждой буквы:
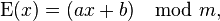 где модуль m– размер алфавита,а пара a иb - ключ шифра. Значение должно быть выбрано таким, что a и m - взаимно простые числа. Функция расшифрования:
где модуль m– размер алфавита,а пара a иb - ключ шифра. Значение должно быть выбрано таким, что a и m - взаимно простые числа. Функция расшифрования:
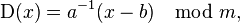 где
где 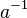 — обратное к aчисло по модулю m.
Примеры шифрования и расшифрования
В следующих примерах используются латинские буквы от A до Z, соответствующие им численные значения приведены в таблице.
— обратное к aчисло по модулю m.
Примеры шифрования и расшифрования
В следующих примерах используются латинские буквы от A до Z, соответствующие им численные значения приведены в таблице.
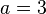 ,
, 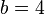 и
и 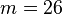 , так как в используемом алфавите 26 букв. Только на число
, так как в используемом алфавите 26 букв. Только на число  наложены ограничения, так как оно должно быть взаимно простым с 26. Значение
наложены ограничения, так как оно должно быть взаимно простым с 26. Значение 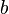 может быть любым, только если
может быть любым, только если  не равно единице, так как это сдвиг шифра.
не равно единице, так как это сдвиг шифра. . Первый шаг шифрования — запись чисел, соответствующих каждой букве сообщения.
. Первый шаг шифрования — запись чисел, соответствующих каждой букве сообщения.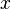 найдем значение
найдем значение  . После нахождения значения
. После нахождения значения  для каждого символа возьмем остаток от деления
для каждого символа возьмем остаток от деления  на 26.
на 26.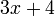
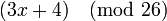
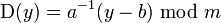 , где
, где 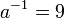 ,
, 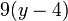 и взять остаток от деления этого числа на 26.
и взять остаток от деления этого числа на 26.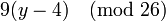
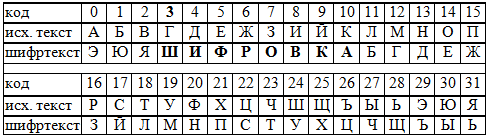 Таблица 4. Таблица замен символов для системы шифрования Цезаря при K=3, M=32 и ключевом слове «ШИФРОВКА»
Далее с помощью табл. 4 шифруем побуквенно слово «НЕПТУН». В результате получаем шифротекст: «ДФЖЛМД».
Для расшифрования получателю отправляют ключевое слово и ключ К, при помощи которого он создаёт шифротекст и расшифровывает посланную информацию.
Таблица 4. Таблица замен символов для системы шифрования Цезаря при K=3, M=32 и ключевом слове «ШИФРОВКА»
Далее с помощью табл. 4 шифруем побуквенно слово «НЕПТУН». В результате получаем шифротекст: «ДФЖЛМД».
Для расшифрования получателю отправляют ключевое слово и ключ К, при помощи которого он создаёт шифротекст и расшифровывает посланную информацию.