Примеры выполнение заданий курсовой работы по теме «Сила давления жидкости на плоские поверхности».

Пример 1. Прямоугольная крышка AB (рис. 2.11), расположенная под углом a = 60^o к горизонту, перекрывает патрубок закрытого резервуара с водой. Высота патрубка h = 600 мм, ширина b = 400 мм. Крышка может поворачиваться вокруг шарнира A. Высота уровня воды над шарниромa a = 200 мм. Давление на поверхности воды соответствует показанию U-образного ртутного манометра h _рт =80 мм.

Определить силу натяжения троса T для удержания крышки AB в закрытом положении. Угол натяжения троса b = 45^o. Принять плотность воды r = 10³ кг/м³.

 

Решение.

 

Для определения силы натяжения троса T для удержания крышки AB в закрытом положении необходимо определить силу от внешнего давления R ₀ и силу давления воды R _ж.

Рассмотрим аналитический способ расчета давления и центра давления. Расчет проведем в следующей последовательности:

- рассчитывается сила давления жидкости и сила внешнего давления, при этом на чертеже обозначаются центральные оси плоской стенки и глубина погружения центра тяжести стенки от свободной поверхности (h _C);

- определяются точки приложения сил, на чертеже обозначается точка приложения силы давления жидкости (центр давления) и глубина погружения центра давления h _D;

- показывается направление действия сил, при этом сила давления направлена по нормали к поверхности.

Определим силу от внешнего давления R ₀. Значение давления p₀ по показанию U-образного манометра получим из условия равновесия жидкости относительно плоскости уровня 0-0. Давление p₀ является избыточным:

; .

Значение p₀ можно получить другим способом – перевести показание манометра 80 мм. рт. ст. в Па:

.

 

Сила от внешнего давления есть , где A – площадь крышки в м². Из чертежа . Тогда .

Покажем линию действия и точку приложения силы R ₀. Эпюра давления p ₀ представляет собой равномерно распределенную прямоугольную нагрузку; равнодействующая от такой нагрузки проходит через центр тяжести эпюры и приложена в центре тяжести стенки на глубина. h _C (рис. 2.11б). Сила R ₀ направлена по нормали из жидкости на стенку, как сила внешнего, избыточного давления.

Определим силу давления жидкости , где ; глубину погружения центра тяжести стенки в жидкость h _C отсчитываем от свободной поверхности (рис. 2.11а). То есть .

Подставляя числовые значения, получаем

.

Рассчитаем глубину погружения центра давления h _D (точки приложения силы R _ж).

, где - центральный момент инерции прямоугольной крышки относительно горизонтальной оси. Подставляя числовые значения, получаем h _D = 0,56 м.

Эксцентриситет (понижение центра давления относительно центра тяжести) (рис. 2.11а).

Рассчитаем силу натяжения троса T. Для этого составим уравнение моментов относительно точки A . В этом случае Отсюда находим

Ответ: для удержания крышки в закрытом положении необходима сила натяжения троса

 

Пример 2. В торцевой стенке цистерны, заполненной бензином, предусмотрена плоская круглая крышка диаметром d = 1,6 м, укрепленная при помощи болтов. Определить силу давления бензина на крышку и точку приложения силы, если высота уровня бензина над нижней кромкой крышки H = 2,0 м. На поверхности бензина действует вакуумметрическое давление p _вак = 0,2 ат. Принять плотность бензина r_бенз = 720 кг/м³ (рис. 2.12).

 

 

Решение.

 

Для определения равнодействующей воспользуемся аналитическим методом. В этом случае , или .

Определим силу внешнего вакуумметрического давления , где A – площадь крышки;

Тогда .

Данная сила приложена в центре тяжести крышки (т. С) и направлена по нормали внутрь жидкости, как сила отрицательного вакуумметрического давления.

Определим силу давления бензина на крышку , где h _C – глубина погружения центра тяжести крышки, отсчитанная от свободной поверхности. Согласно геометрии чертежа h _C = H - d/2 =1,2 м. Тогда

Сила давления приложена в центре давления на глубине h _D и направлена по нормали из жидкости. При этом глубина погружения центра давления есть . Подставив числовые значения получаем h _D = 1,2+0,13 = 1,33 м. Эксцентриситет при этом .

Определим величину и положение равнодействующей путем векторного сложения 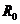и . В числовом виде R _равн = R ₀ – R _ж = 22,5 кН.

Положение равнодействующей определи исходя из теоремы Вариньона: момент от равнодействующей равен сумме моментов составляющих. Таким образом:

;

; отсюда

Равнодействующая направлена по нормали внутрь жидкости.

Ответ. R _равн = 22,5 кН,

 

Пример 3. Определить равнодействующую давления воды и положение центра давления на грани напорной грани плотины ABC, удерживающей напоры: H ₁ = 3,0 м; H ₂ = 2,0 м. Угол наклона наклонной грани плотины a = 60^°. Длина плотины в плоскости, перпендикулярной плоскости чертежа, l = 10 м (рис. 2.13). Решение выполнить графо-аналитическим методом.

 

 

Решение.

 

Графо-аналитический метод решения предусматривает выполнение чертежа в масштабе. Представим в в удобном выбранном масштабе сечение плотины и действующие напоры. Равнодействующая давления воды на грани плотины определяется путем векторного сложения сил, действующих на наклонную (R _AB) и вертикальную (R _BC) грани плотины:

Расчет силы давления на плоские поверхности графо-аналитическим методом проведем по следующей методике.

- Определим давление воды в характерных точках плотины ABC:

; ; ;

;

.

- Строим эпюры гидростатического давления воды. В выбранном масштабе откладываем величину давления в точках A, B, и C. Давление действует нормально к поверхности (рис. 2.13).

Эпюра давления на наклонную грань плотины представляет собой равномерную нагрузку в виде треугольника. Основание треугольника соответствует давлению отложенному по нормали к наклонной грани.

При построении эпюры давления на вертикальную грань, то же давление в точке B откладывается нормально к вертикальной грани плотины. В точке C откладываем давление . Для вертикальной грани эпюра давления представляет равномерную нагрузку в виде трапеции (рис. 2.13).

Рассчитаем силы давления воды на грани плотины:

;

.

Определим линию действия сил и . Сила давления жидкости проходит через центр тяжести эпюры гидростатического давления. Центр тяжести эпюры в виде треугольной нагрузки расположен на расстоянии 2/3 высоты треугольника, т.е. на расстоянии . Находим в масштабе центр тяжести треугольника и показываем линию действия силы . Сила проходит через центр тяжести треугольника и приложена нормально к наклонной грани плотины в центре давления (точка D₁). Отмечаем на чертеже глубину погружения центра давления .

Для определения положения центра тяжести эпьры в виде трапеции рассмотрим геометрический способ определения центра тяжести трапеции:

· к меньшему основанию трапеции на его продолжение в любую сторону добавляем большее основание трапеции;

· к большему основанию в противоположную сторону прибавляем меньшее основание;

· полученные точки соединяются прямой;

· через середины оснований трапеции проводится дополнительная линия;

· точка пересечения двух линий построения является центром тяжести эпюры давления в виде трапеции.

Согласно данному методу показываем центр тяжести трапеции и через данную точку проводим силу по нормали к вертикальной грани. С учетом масштаба действующих напоров .

Определим величину и линию действия равнодействующей сил давления R путем векторного сложения сил и . Для данного случая точка пересечения составляющих сил (т. К) вынесена за пределы чертежа, а точка действия равнодействующей (т. D) перенесена по линии действия силы R до ее пересечения с гранью плотины. Глубину погружения центра давления h_D определяем по масштабу. В данном случае h _D = 3,5 м.

Числовое значение равнодействующей найдем по теореме косинусов .

Ответ. Сила давления воды на напорную грань плотины R = 1251,2 кН, глубина погружения центра давления h _D = 3,5 м.

 

Тема № 3. «Сила давления жидкости на криволинейные поверхности».

 

Задание 1. Определить величину и угол наклона силы давления бензина на полусферическую крышку закрытого резервуара (рис. 3.1), если радиус полусферы r, а показания пьезометра выведенного на уровень нижней кромки крышки H. Принять плотность бензина r_бенз=800 кг/м³. Требуемые числовые значения берутся из таблицы 3.

 

 

Задание 2. Определить силу давления масла на цилиндрическую стенку резервуара AB (рис. 3.2), угол наклона силы и глубину погружения центра давления, если глубина заполнения резервуара H, радиус цилиндрической части r, секторальный угол равен 90^°; длина образующей цилиндрической поверхности L. Принять плотность масла r_масл=860 кг/м³. Требуемые числовые значения берутся из таблицы 3

 

Задание 3. Определить величину и угол наклона к горизонту равнодействующей давления воды на криволинейную стенку AB резервуара (рис. 3.3), если ширина резервуара B, напоры воды H₁, H₂. Требуемые числовые значения берутся из таблицы 3.

 

 

Задание 4. Определить силу давления бензина на полусферическое дно цилиндрического резервуара (рис. 3.4) радиусом r, если показание манометра, установленного на расстоянии h от дна резервуара p_ман. Принять плотность бензина r_бенз=720 кг/м³. Требуемые числовые значения берутся из таблицы 3.

 

 

Задание 5. Определить усилие F, которое нужно приложить к полусферической крышке резервуара с водой (рис. 3.5) для удержания ее в закрытом положении, если радиус сферы r. Крышка поворачивается вокруг шарнира в точке A. Показание пьезометра, установленного на уровне шарнира равно h. Требуемые числовые значения берутся из таблицы 3.

 

Задание 6. Определить силу давления воды на верхнюю и нижнюю половины сферического резервуара радиусом r, полностью заполненного водой, а также растягивающие усилие в болтах фланцевого соединения (количество болтов N), если показание манометра установленного под углом 45^° в нижней части резервуара равно p_ман (рис. 3.6). Требуемые числовые значения берутся из таблицы 3.

 

 

Задание 7. Определить величину, угол наклона и глубину центра давления для равнодействующей давления воды на криволинейную стенку AB (рис. 3.7) длиной L. Действующий напор H. Криволинейная стенка представляет собой часть цилиндрической поверхности с секторным углом j. Требуемые числовые значения берутся из таблицы 3.

 

 

Задание 8. Определить величину, угол наклона к горизонту и глубину центра давления воды на криволинейную стенку AB (рис. 3.8) длиной L, удерживающую напор H. Криволинейная стенка представляет собой часть цилиндрической поверхности с секторным углом j. Требуемые числовые значения берутся из таблицы 3.

 

Задание 9. Определить равнодействующую сил давления воды, угол наклона ее к горизонту и глубину погружения центра давления для цилиндрической поверхности AB с секторным углом j. Длина поверхности L. Действующий напор слева H, справа h = H /2 (рис. 3.9). При решении представить чертеж в виде вертикального сечения криволинейной поверхности. Требуемые числовые значения берутся из таблицы 3.

 

 

Задание 10. Определить величину и угол наклона к горизонту равнодействующей сил давления воды на устройство в виде цилиндрического затвора (рис. 3.10), если диаметр цилиндра D, действующий напор слева H, справа h = H /2. Длина цилиндрического затвора L.

 

Таблица 3.

Величины	Последняя цифра зачетной книжки
	r, м	0,10	0,15	0,20	0,25	0,3	0,35	0,4	0,45	0,5	0,55
H, м	0,70	0,75	0,80	0,85	0,90	0,95	1,00	1,05	1,10	1,15
	H, м	0,6	0,65	0,7	0,75	0,8	0,85	0,9	0,95	1,00	1,1
r, м	0,4	0,45	0,5	0,55	0,6	0,65	0,70	0,75	0,80	0,85
L, м	0,8	0,9	1,0	1,1	1,2	1,3	1,4	1,5	1,6	1,7
	B, м	2,2	2,4	2,6	2,8	3,0	3,2	3,4	3,6	3,8	4,0
H1, м	1,6	1,7	1,8	1,9	2,0	2,1	2,2	2,3	2,4	2,5
H2, м	0,80	0,85	0,90	0,95	1,0	1,05	1,10	1,15	1,20	1,25
	r, м	0,20	0,25	0,30	0,35	0,4	0,45	0,50	0,55	0,60	0,65
h, м	0,60	0,65	0,70	0,75	0,8	0,85	0,90	0,95	1,00	1,1
pман, ат	0,08	0,09	0,10	0,11	0,12	0,13	0,14	0,15	0,16	0,17
	r, м	0,1	0,15	0,2	0,25	0,3	0,35	0,4	0,45	0,5	0,55
h, м	0,4	0,45	0,5	0,55	0,6	0,65	0,7	0,75	0,8	0,85
	r, м	0,15	0,20	0,25	0,30	0,35	0,40	0,45	0,50	0,55	0,60
N
pман, ат	0,07	0,08	0,09	0,10	0,11	0,12	0,13	0,14	0,15	0,16
	L, м
H, м					4,0
j, град
	L, м	1,5	2,0	2,5	3,0	3,5	4,0	4,5	5,0	5,5	6,0
H, м	0,75	1,00	1,25	1,5	1,75	2,00	2,25	2,50	2,75	3,00
j, град
	j, град
L, м	2,4	2,6	2,8	3,0	3,2	3,4	3,6	3,8	4,0	4,2
H, м	1,2	1,3	1,4	1,5	1,6	1,7	1,8	1,9	2,0	2,2
	D, м	0,5	0,6	0,7	0,8	0,9	1,0	1,1	1,2	1,3	1,4
H, м	0,8	0,9	1,0	1,1	1,2	1,3	1,4	1,5	1,6	1,7
L, м	2,0	2,5	3,0	3,5	4,0	4,5	5,0	5,5	6,0	7,0