 Все чаще и чаще в научной литературе отмечается плодотворное влияние на человека конструкций, пропорционированных по золотому сечению. Причём, имеются в виду любые конструкции и предметы, созданные человеком. От примитивной ложки до грандиозного дворца.
Становится ясно, что пропорционирование частей зданий и сооружений, соответствующее природным пропорциям и пропорциям человека, его восприятию действительности и ощущениям, является важнейшим фактором нормального функционирования человеческого организма. Но как вычислять «золотые размеры»? Из-за того, что в золотых пропорциях все числа иррациональные, вычислять их в уме или даже на калькуляторе сложно или невозможно. Тут справится только современный компьютер. Но программу для компьютера пока составить невозможно, поскольку принципы применения золотой пропорции ещё только начинают выступать из тумана. Но как выходили из ситуации наши предки? Анализ абсолютно всех древних сооружений, начиная с египетских пирамид, показывает присутствие Золотой пропорции, и многовариантность её применения сбивает с толку. А самые «свежие» из уцелевших золотосечённых сооружений – древнерусские церкви и храмы!!! Издавна и аж до 18-го века на Руси строили согласно золотым пропорциям! Только Пётр I положил конец «беспорядку», приравняв казённую сажень (217,6см) к 7 английским футам (213,360 см). В 1835г. Николай I вообще запретил остальные сажени, а в 1924 г. была введена метрическая система.
Значит, гораздо проще попробовать восстановить древнерусскую измерительную систему, чем сочинять навороченные программы для компьютера и таскать его с собой. Непонятно ещё, чем закончится такое «изобретение велосипеда».
Чтобы понять суть и смысл измерения в древнерусских саженях, придётся немного окунуться в математику и геометрию. Совсем немного, просмотрите хоть по диагонали все формулы.
Давно установлено существование загадочного «Золотого числа» Ф.
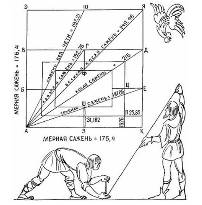
Практическое знакомство с Золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки. Из точки В восставляется перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции. Все чаще и чаще в научной литературе отмечается плодотворное влияние на человека конструкций, пропорционированных по золотому сечению. Причём, имеются в виду любые конструкции и предметы, созданные человеком. От примитивной ложки до грандиозного дворца.
Становится ясно, что пропорционирование частей зданий и сооружений, соответствующее природным пропорциям и пропорциям человека, его восприятию действительности и ощущениям, является важнейшим фактором нормального функционирования человеческого организма. Но как вычислять «золотые размеры»? Из-за того, что в золотых пропорциях все числа иррациональные, вычислять их в уме или даже на калькуляторе сложно или невозможно. Тут справится только современный компьютер. Но программу для компьютера пока составить невозможно, поскольку принципы применения золотой пропорции ещё только начинают выступать из тумана. Но как выходили из ситуации наши предки? Анализ абсолютно всех древних сооружений, начиная с египетских пирамид, показывает присутствие Золотой пропорции, и многовариантность её применения сбивает с толку. А самые «свежие» из уцелевших золотосечённых сооружений – древнерусские церкви и храмы!!! Издавна и аж до 18-го века на Руси строили согласно золотым пропорциям! Только Пётр I положил конец «беспорядку», приравняв казённую сажень (217,6см) к 7 английским футам (213,360 см). В 1835г. Николай I вообще запретил остальные сажени, а в 1924 г. была введена метрическая система.
Значит, гораздо проще попробовать восстановить древнерусскую измерительную систему, чем сочинять навороченные программы для компьютера и таскать его с собой. Непонятно ещё, чем закончится такое «изобретение велосипеда».
Чтобы понять суть и смысл измерения в древнерусских саженях, придётся немного окунуться в математику и геометрию. Совсем немного, просмотрите хоть по диагонали все формулы.
Давно установлено существование загадочного «Золотого числа» Ф.
Практическое знакомство с Золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки. Из точки В восставляется перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции.
 Точное значение Ф находится математическим путём как корень квадратного уравнения, получаемого при делении отрезка в крайнем и среднем отношениях, то есть в соотшонении золотой пропорции:
Точное значение Ф находится математическим путём как корень квадратного уравнения, получаемого при делении отрезка в крайнем и среднем отношениях, то есть в соотшонении золотой пропорции:
 (a+c)/c=c/a=Ф Это золотая пропорция. Решений для чисел a и c бесконечное множество, и все они будут иррациональными (хотя одно число может быть и целым). А вот решение для числа Ф всего одно:
Ф=(1 + V5)/2 =1,6180339887498948482045868343656…(V5-это квадратный корень из5)
Правда, у вышеупомянутого квадратного уравнения есть ещё один корень (1- V5)/2 = - 1/Ф, но поскольку он отрицательный, а оба числа a и c у нас положительные, это решение отбрасываем.
Ф-число иррациональное бесконечное.
Обратная величина 1/Ф=0,6180339887498948482045868343656…
Квадрат Ф2= 2,6180339887498948482045868343656…
Все знаки после запятой одинаковые… Вот загадочное число, не правда ли? Но это ещё не всё.
Известный числовой ряд Фибоначчи (открыт в XIII веке), где каждый последующий член ряда равен сумме двух предыдущих, имеет вид:
1,2,3,5,8,13,21,34, 55, 89,... 377, 610,987,1598,2885,...
Нетрудно заметить, что с увеличением порядковых номеров членов деление последующего члена на предыдущий всё более приближается к золотому числу Ф:
3:2=1,5; 5:3=1,666; 21:13=1,615; 55:34=1,617;...610:377= 1,618037....
Золотое иррациональное число Ф было известно еще в Древней Греции как основа образования бесконечного ряда величин, обладающего свойствами чисел Фибоначчи, получаемых в результате умножения или деления базисной единицы 1 на золотое число Ф. Ветвь ряда, образуемая последовательным умножением на Ф, называется восходящей: 1; 1,618; 2,618; 4,236; 6,854; 11,090; 17,944; 29,034... а другая часть ряда, образуемая последовательным делением на Ф, называется нисходящей: 1; 0,618; 0,382; 0,236; 0,146; 0,090; 0,056; 0,034....
Само число 1, первые три члена восходящего ряда и семь членов ряда нисходящего составляют греческий ряд чисел, получивших название "золотая пропорция" или "золотое сечение".
Золотая пропорция — единственная геометрическая прогрессия (конечно, можно взять любое базисное число вместо 1 и будет другой ряд, но множитель 1.618… единственный), у которой есть и свойства ряда Фибоначчи: каждый последующий член ряда получается, как и числа Фибоначчи, сложением двух предыдущих членов, а весь ряд, за исключением базисной 1, состоит из иррациональных чисел. Причём, ряд бесконечен в обе стороны, в отличие от классических рядов Фибоначчи, имеющих начало.
Откуда возникли представления о делении отрезков в крайнем и среднем отношениях, позволяющем получать золотое число Ф и пропорцию, названную Леонардо да Винчи «золотым сечением», нам неизвестно.
Итак, загадочное число Ф вычислено. Но зачем оно нам понадобилось?
Оказывается, всё в природе, включая человека, создано согласно пропорциям золотого сечения.
Мы любим красоту. Наше тело интуитивно чувствует золотую пропорцию. Всё, что нам кажется красивым, обладает свойствами золотого сечения. Будь то природный ландшафт, картина художника или тело человека. Почему это так, пока однозначного ответа нет. Эзотерики сразу приводят в качестве доказательства «частоту вибраций», создаваемых разными телами, и у золотосечённых тел она вроде-бы одинаковая. Некоторые утверждают, что золотосечённые тела наоборот поглощают (или пропускают) все частоты одинаково, благодаря чему имеют сбалансированную информацию. Встречалось и такое выражение про современные простройки: «порождают стоячие волны, губительно действующие на сознание и организм человека». Учёные от науки пока совсем молчат по этому поводу.
За последние десятилетия многочисленными исследователями были установлены повсеместные проявления закона золотых пропорций от Космоса до Микромира.
Во Вселенной все известные человечеству галактики и все тела в них существуют в форме спирали, соответствующей формуле золотого сечения. Русский астроном Бутусов в 1978 г. установил, что отношение периодов обращения соседних планет вокруг Солнца равны либо золотой пропорции 1,618, либо ее квадрату 2,618.
Соотношения золотой пропорции исследователи находят в морфологической структуре растений, птиц, животных, человека.
Закономерности золотой пропорции обнаруживаются и в организации неорганической природы, например, структура талой воды, практически соответствует треугольнику золотой пропорции.
Таким образом, проявление принципа золотых пропорций наблюдается повсеместно в природе от бесконечно больших галактик до бесконечно малых клеток и атомов.
Фигура человека, исследованная немецким исследователем проф. Цейзингом в 1855 г. явилась ярким примером золотых пропорций.
Дальше придётся ещё бегло познакомиться с понятием вурфных соотношений.
Для блока, состоящего из трех элементов с длинами а, b, c вурфное отношение W(а, b, с) вычисляется по формуле:
W(a,b,с)=(а+b)(b+с)/b(a+b+с).
При этом другой блок — с другими размерами и другими соотношениями элементов — а', b', с' будет ему конформно симметричен, если величины их вурфов будут равны, т.е. если: W(a, b, с)=W(a', b',с').
Путем преобразований такие блоки могут быть совмещены один с другим с полным совпадением всех их точек.
В процессе роста размеры частей тела человека и их соотношения все время меняются. Причём, эти изменения следуют принципам конформно-симметричных преобразований. Например, если взять соотношения стопы, голени и бедра в возрасте 1 года, 10 и 20 лет, то изменения выглядят так: 1:1,27:1,40; 1:1,34:1,55; 1:1,39:1,68.
Рост различных частей тела не протекает равномерно. Голень и бедро увеличиваются значительно больше, нежели стопа, пропорции тела человека все время меняются. Вурфные же соотношения для любого возраста вычисляются с одним и тем же значением (W(1;1,27;1,40)=1,30; W(1;1,34;1,55)=1,30; W(1;1,39;1,68)=1,30) и оказываются неизменными на протяжении всего времени роста. Постоянная и неизменная величина вурфа свидетельствует о преобразовании форм нашего тела по принципам конформной симметрии. Такая же картина открывается и для других блоков: плеча — предплечья — кисти; фаланг пальцев; туловища, верхней и нижней конечностей тела и т.д.
Значения вурфов немного варьируются, составляя в среднем величину W = 1,31. В идеальном случае В.Петухов указывает W = 1,309, что при выражении через величину золотого сечения равно Ф2/2. Он называет его "золотым вурфом".
Вурфные пропорции позволяют, следовательно, выявить конформно-симметричные группы, иными словами, группы родственных отношений с единым исходным началом. Обычные двучленные пропорции показывают лишь различия, вурфные — общность некоторого множества трехчленных соотношений.
Если пропорции окружающих нас произведений архитектуры, принадлежат к случайным группам, как в большинстве современных сооружений, то человек оказывается в среде, пропорциональная структура которой по своей симметрии ему не свойственна. Такая Среда, не обладающая ни одной из характеристических групп симметрии человека, чаще всего не воспринимается им, а нередко отвергается. Вот где корень неблагоприятного психофизического воздействия Среды на человека, а не только в том, что жилые дома представляют собой набор однотипных "коробок". Тоже самое можно сказать и про притягательность и красоту любых объектов, нас окружающих.
Многие ученые уже 100 лет усердно бьются над расшифровкой и восстановлением утерянных русских саженей. Значительный прорыв произошёл после 1970г, когда в Новгороде у церкви Параскевы Пятницы был найден обломок мерила новгородского зодчего. В процессе исследований мерила сначала Пилецкому А.А., а потом Черняеву А.Ф, удалось не только восстановить его полностью, но и показать, что оно являлось одновременно измерительным и соизмерительным инструментом. На одной грани были нанесены мерки всех саженей, а остальные три грани в комплексе с первой представляли собой своеобразную логарифмическую линейку, позволяющую очень просто подбирать золотые пропорции! Заодно были вычислены недостающие сажени и уточнены размеры известных. Список саженей приведён ниже. Многие названия восстановить не удалось, многие имели по нескольку названий, поэтому придуманы новые или использовано одно из старых названий.
Также существовали более мелкие измерительные величины: полсажени (1/2 сажени), локоть (1/4 сажени), пядь (1/8 сажени), пясть (1/16 сажени), вершок (1/32 сажени). На основе саженей и их долей, а также последовательным умножением на 2 всех саженей, составлена матрица, названная «Русский Всемер»:
(a+c)/c=c/a=Ф Это золотая пропорция. Решений для чисел a и c бесконечное множество, и все они будут иррациональными (хотя одно число может быть и целым). А вот решение для числа Ф всего одно:
Ф=(1 + V5)/2 =1,6180339887498948482045868343656…(V5-это квадратный корень из5)
Правда, у вышеупомянутого квадратного уравнения есть ещё один корень (1- V5)/2 = - 1/Ф, но поскольку он отрицательный, а оба числа a и c у нас положительные, это решение отбрасываем.
Ф-число иррациональное бесконечное.
Обратная величина 1/Ф=0,6180339887498948482045868343656…
Квадрат Ф2= 2,6180339887498948482045868343656…
Все знаки после запятой одинаковые… Вот загадочное число, не правда ли? Но это ещё не всё.
Известный числовой ряд Фибоначчи (открыт в XIII веке), где каждый последующий член ряда равен сумме двух предыдущих, имеет вид:
1,2,3,5,8,13,21,34, 55, 89,... 377, 610,987,1598,2885,...
Нетрудно заметить, что с увеличением порядковых номеров членов деление последующего члена на предыдущий всё более приближается к золотому числу Ф:
3:2=1,5; 5:3=1,666; 21:13=1,615; 55:34=1,617;...610:377= 1,618037....
Золотое иррациональное число Ф было известно еще в Древней Греции как основа образования бесконечного ряда величин, обладающего свойствами чисел Фибоначчи, получаемых в результате умножения или деления базисной единицы 1 на золотое число Ф. Ветвь ряда, образуемая последовательным умножением на Ф, называется восходящей: 1; 1,618; 2,618; 4,236; 6,854; 11,090; 17,944; 29,034... а другая часть ряда, образуемая последовательным делением на Ф, называется нисходящей: 1; 0,618; 0,382; 0,236; 0,146; 0,090; 0,056; 0,034....
Само число 1, первые три члена восходящего ряда и семь членов ряда нисходящего составляют греческий ряд чисел, получивших название "золотая пропорция" или "золотое сечение".
Золотая пропорция — единственная геометрическая прогрессия (конечно, можно взять любое базисное число вместо 1 и будет другой ряд, но множитель 1.618… единственный), у которой есть и свойства ряда Фибоначчи: каждый последующий член ряда получается, как и числа Фибоначчи, сложением двух предыдущих членов, а весь ряд, за исключением базисной 1, состоит из иррациональных чисел. Причём, ряд бесконечен в обе стороны, в отличие от классических рядов Фибоначчи, имеющих начало.
Откуда возникли представления о делении отрезков в крайнем и среднем отношениях, позволяющем получать золотое число Ф и пропорцию, названную Леонардо да Винчи «золотым сечением», нам неизвестно.
Итак, загадочное число Ф вычислено. Но зачем оно нам понадобилось?
Оказывается, всё в природе, включая человека, создано согласно пропорциям золотого сечения.
Мы любим красоту. Наше тело интуитивно чувствует золотую пропорцию. Всё, что нам кажется красивым, обладает свойствами золотого сечения. Будь то природный ландшафт, картина художника или тело человека. Почему это так, пока однозначного ответа нет. Эзотерики сразу приводят в качестве доказательства «частоту вибраций», создаваемых разными телами, и у золотосечённых тел она вроде-бы одинаковая. Некоторые утверждают, что золотосечённые тела наоборот поглощают (или пропускают) все частоты одинаково, благодаря чему имеют сбалансированную информацию. Встречалось и такое выражение про современные простройки: «порождают стоячие волны, губительно действующие на сознание и организм человека». Учёные от науки пока совсем молчат по этому поводу.
За последние десятилетия многочисленными исследователями были установлены повсеместные проявления закона золотых пропорций от Космоса до Микромира.
Во Вселенной все известные человечеству галактики и все тела в них существуют в форме спирали, соответствующей формуле золотого сечения. Русский астроном Бутусов в 1978 г. установил, что отношение периодов обращения соседних планет вокруг Солнца равны либо золотой пропорции 1,618, либо ее квадрату 2,618.
Соотношения золотой пропорции исследователи находят в морфологической структуре растений, птиц, животных, человека.
Закономерности золотой пропорции обнаруживаются и в организации неорганической природы, например, структура талой воды, практически соответствует треугольнику золотой пропорции.
Таким образом, проявление принципа золотых пропорций наблюдается повсеместно в природе от бесконечно больших галактик до бесконечно малых клеток и атомов.
Фигура человека, исследованная немецким исследователем проф. Цейзингом в 1855 г. явилась ярким примером золотых пропорций.
Дальше придётся ещё бегло познакомиться с понятием вурфных соотношений.
Для блока, состоящего из трех элементов с длинами а, b, c вурфное отношение W(а, b, с) вычисляется по формуле:
W(a,b,с)=(а+b)(b+с)/b(a+b+с).
При этом другой блок — с другими размерами и другими соотношениями элементов — а', b', с' будет ему конформно симметричен, если величины их вурфов будут равны, т.е. если: W(a, b, с)=W(a', b',с').
Путем преобразований такие блоки могут быть совмещены один с другим с полным совпадением всех их точек.
В процессе роста размеры частей тела человека и их соотношения все время меняются. Причём, эти изменения следуют принципам конформно-симметричных преобразований. Например, если взять соотношения стопы, голени и бедра в возрасте 1 года, 10 и 20 лет, то изменения выглядят так: 1:1,27:1,40; 1:1,34:1,55; 1:1,39:1,68.
Рост различных частей тела не протекает равномерно. Голень и бедро увеличиваются значительно больше, нежели стопа, пропорции тела человека все время меняются. Вурфные же соотношения для любого возраста вычисляются с одним и тем же значением (W(1;1,27;1,40)=1,30; W(1;1,34;1,55)=1,30; W(1;1,39;1,68)=1,30) и оказываются неизменными на протяжении всего времени роста. Постоянная и неизменная величина вурфа свидетельствует о преобразовании форм нашего тела по принципам конформной симметрии. Такая же картина открывается и для других блоков: плеча — предплечья — кисти; фаланг пальцев; туловища, верхней и нижней конечностей тела и т.д.
Значения вурфов немного варьируются, составляя в среднем величину W = 1,31. В идеальном случае В.Петухов указывает W = 1,309, что при выражении через величину золотого сечения равно Ф2/2. Он называет его "золотым вурфом".
Вурфные пропорции позволяют, следовательно, выявить конформно-симметричные группы, иными словами, группы родственных отношений с единым исходным началом. Обычные двучленные пропорции показывают лишь различия, вурфные — общность некоторого множества трехчленных соотношений.
Если пропорции окружающих нас произведений архитектуры, принадлежат к случайным группам, как в большинстве современных сооружений, то человек оказывается в среде, пропорциональная структура которой по своей симметрии ему не свойственна. Такая Среда, не обладающая ни одной из характеристических групп симметрии человека, чаще всего не воспринимается им, а нередко отвергается. Вот где корень неблагоприятного психофизического воздействия Среды на человека, а не только в том, что жилые дома представляют собой набор однотипных "коробок". Тоже самое можно сказать и про притягательность и красоту любых объектов, нас окружающих.
Многие ученые уже 100 лет усердно бьются над расшифровкой и восстановлением утерянных русских саженей. Значительный прорыв произошёл после 1970г, когда в Новгороде у церкви Параскевы Пятницы был найден обломок мерила новгородского зодчего. В процессе исследований мерила сначала Пилецкому А.А., а потом Черняеву А.Ф, удалось не только восстановить его полностью, но и показать, что оно являлось одновременно измерительным и соизмерительным инструментом. На одной грани были нанесены мерки всех саженей, а остальные три грани в комплексе с первой представляли собой своеобразную логарифмическую линейку, позволяющую очень просто подбирать золотые пропорции! Заодно были вычислены недостающие сажени и уточнены размеры известных. Список саженей приведён ниже. Многие названия восстановить не удалось, многие имели по нескольку названий, поэтому придуманы новые или использовано одно из старых названий.
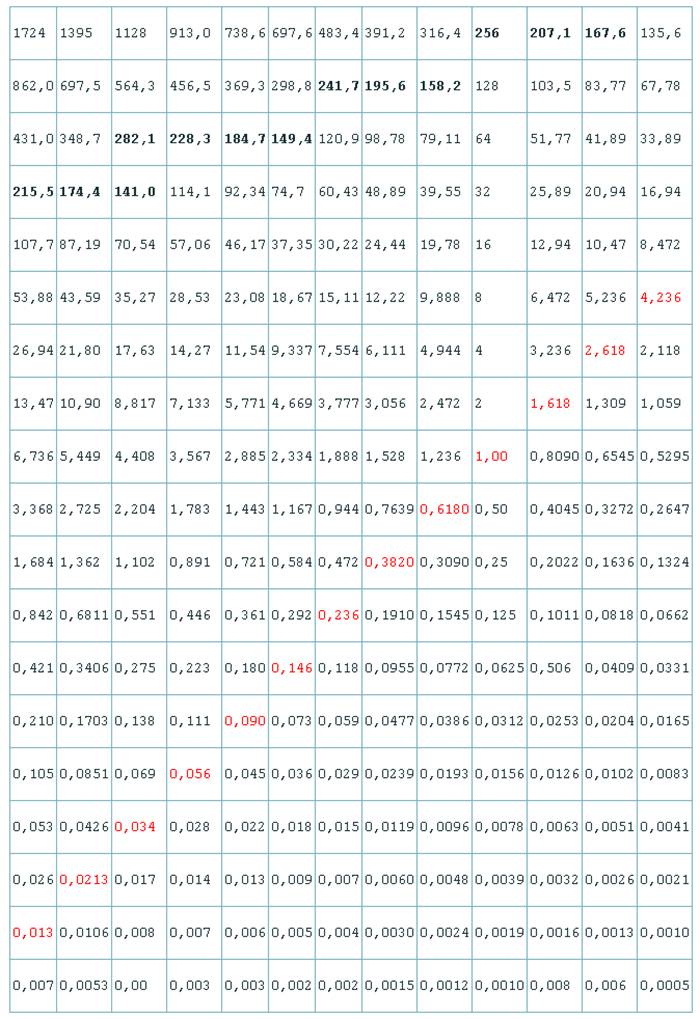
Также существовали более мелкие измерительные величины: полсажени (1/2 сажени), локоть (1/4 сажени), пядь (1/8 сажени), пясть (1/16 сажени), вершок (1/32 сажени). На основе саженей и их долей, а также последовательным умножением на 2 всех саженей, составлена матрица, названная «Русский Всемер»:
 Размеры всех саженей даны в см, выделены красным. Вверху таблицы-названия саженей. Оказалось, что все диагонали слева направо снизу вверх представляют собой ряды Фибоначчи и Золотую пропорцию одновременно. Для примера возьмём диагональ Народной сажени:
67,2+108,8=176,0; 176/108,8=1,618; 108,8/67,2=1,618.
По строкам коэффициент везде 2/Ф = 2/1,618 = 1,236.
Если расположить сажени в порядке возрастания длины, то соседние будут относиться друг к другу с одинаковым коэффициентом 1,059… – так же, как частоты соседних полутонов в музыкальном ряду.
Идея! Поскольку сажени соотносятся между собой так же, как частоты нот, можно попробовать «проиграть» проект дома, предварительно согласовав таблицу саженей с нотами, а размеры дома с длительностью нот. Возможно, дом с гармоничными размерами будет «звучать» приятно. Музыканты, проверяйте!
Матрица может быть продолжена до бесконечности во все стороны - влево и вправо, вверх и вниз.
Легко заметить, что более логичной (с нашей точки зрения) выглядела бы матрица, содержащая диагональ греческого ряда, золотую пропорцию:
…0,382; 0,618; 1; 1,618; 2,618; 11,090; 17,944; 29,034 …122,97; 198,96…
Размеры всех саженей даны в см, выделены красным. Вверху таблицы-названия саженей. Оказалось, что все диагонали слева направо снизу вверх представляют собой ряды Фибоначчи и Золотую пропорцию одновременно. Для примера возьмём диагональ Народной сажени:
67,2+108,8=176,0; 176/108,8=1,618; 108,8/67,2=1,618.
По строкам коэффициент везде 2/Ф = 2/1,618 = 1,236.
Если расположить сажени в порядке возрастания длины, то соседние будут относиться друг к другу с одинаковым коэффициентом 1,059… – так же, как частоты соседних полутонов в музыкальном ряду.
Идея! Поскольку сажени соотносятся между собой так же, как частоты нот, можно попробовать «проиграть» проект дома, предварительно согласовав таблицу саженей с нотами, а размеры дома с длительностью нот. Возможно, дом с гармоничными размерами будет «звучать» приятно. Музыканты, проверяйте!
Матрица может быть продолжена до бесконечности во все стороны - влево и вправо, вверх и вниз.
Легко заметить, что более логичной (с нашей точки зрения) выглядела бы матрица, содержащая диагональ греческого ряда, золотую пропорцию:
…0,382; 0,618; 1; 1,618; 2,618; 11,090; 17,944; 29,034 …122,97; 198,96…
 Тогда один из вертикальных столбцов имел бы такой «красивый» вид:
…0,25; 0,5; 1; 2; 4; 8; 16; 32; 64; 128; 256; 512; 1024…
И можно было б выбрать очень похожий набор саженей, в том же диапазоне. Они выделены жирным.
Разгадка в том, что матрицы такой в Древней Руси не знали, и более логично им было выбрать соответствие саженей размерам человека. Если принять народную сажень равной росту зодчего, то каждый мог пропорционально ей вычислить остальные сажени. Делалось это разными очень простыми методами, вообще без применения цифр и вычислений (геометрически). Несколько таких методов можно найти в источниках (ссылки в конце статьи). Ну а нам ближе цифры, будем опираться на них.
Видимо, со временем для удобства приняли единую саженную систему, ориентированную на рост среднего человека – 176см, ему приравняли сажень народную. Вот только как хранили этот «эталон», пока неизвестно. Не исключено, что это была одна их царских реликвий в виде жезла или трости. Чтобы не наломать дров, пока и мы будем опираться на этот «саженный стандарт».
Система русских саженей – наследие древней цивилизации, развивавшейся по принципам взаимосвязи всего вокруг. Нам, потомкам технократической цивилизации, потерявшим связь с Природой, невозможно понять суть и смысл тонких процессов, происходящих во Вселенной, а также устройства её самой. Мы привыкли всё делить на составляющие, разбирать, чтобы понять устройство. А нужно наоборот объединять, чтобы понять целое, создать гармонию. Система русских саженей позволяет вычислять гармоничные для Природы пропорции и творить гармонию, не вникая в процесс пропорционирования по Золотой пропорции. На данный момент восстановлены не все принципы строительства по саженям. Но того, что уже есть, вполне достаточно для сооружения несложных строений.
Итак, общие правила применения русских саженей (в основном касаемо строительства домов):
1. Делить сажень и получающиеся доли для вычисления более мелких размеров можно только на 2. При строительстве домов минимальная доля – 1/32 – вершок. Дальше сажень не делится. Вершок можно делить на любое число. Если делать в саженях мелкие предметы, можно делить на 2 до бесконечности.
2. Любой объект проектировался с использованием минимум 3-х разных гармонично связанных саженей: отдельно по высоте, ширине и длине. Чаще всего их число было 5-7, то есть внутренние размеры делались по другим гармонично связанным саженям.
3. Все параметры объектов замерялись только целым, как бы квантованным, числом измерительных инструментов - саженей, локтей, вершков и т.д. Например, длина здания равнялась 12 саженям малым по 142,4 см, что в измерении метром равно 17,088 м. Ширина равна четырем полуторным простым саженям по 150,8 х 1,5 = 2,262х4 м, а в измерении метром 9,048 м. Наконец, высота равна двум простым саженям по 150,8 см или 3,016 м. Таким образом, параметры объектов, отмеренные целым числом саженей, всегда оказываются дробными при измерении стандартным метром. Эта особенность систематически фиксируется при замерах метром всех древнеегипетских сооружений. А потому можно повториться, что достигнуть понимания структуры полуразрушенных пирамид без знания гармонии измерительных инструментов, их породивших, невозможно.
4. Допустимо вводить коэффициенты 1,5; 2; 2,5 к значению сажени, и измерять все оси соответственно полуторными, двойными, двух с половинными саженями, но этот метод не применяется в жилом строительстве.
5. При строительстве жилых зданий по всем осям снаружи берётся четное целое количество саженей, для сакральных сооружений (храмы, часовни, церкви, гробницы) нечетное, и желательно кратное 7 или 11.
6. Внутри зданий допустимо мерить дробными частями саженей, соответственно чётным или нечётным количеством.
7. Сначала подбирается высота, потом гармоничная ей ширина, потом гармоничная высоте и ширине длина (о методах подбора ниже).
8. Все размеры измеряются по выступающим частям: пристройка, ступени, козырёк, водосточная система, крест на храме, флюгер на крыше и т.д. – всё учитывается. Высота определяется по самой высокой точке дома, например конёк, а если в торце конька сооружён петух, - то по нему. Если к дому примыкает башня, высота которой превышает высоту дома, то высота Творения определяется по самой верхней точке башни. Дымоходы и вентиляционные трубы в расчёт не принимаются.
Если цоколь более 20 см, то высота меряется 2-мя разными саженями: отдельно от цоколя и отдельно от земли. Если дом на склоне, то с обоих сторон высота меряется по разным саженям. Если перепад высот менее 3%-не обращать внимания. Внутренняя высота меряется от чистового пола до потолка. При наклонном потолке-до наивысшей точки.
Длину ската крыши также лучше сделать по сажени. На изменения в расчетах она не влияет. Но при вылете свеса кровли более чем на 1/3 от высоты здания, ширину здания уже нужно мерить по ширине свесов, а также учитывать по сажени расстояние от свеса до земли (нулевой отметки здания, фундамента или цоколя).
9. Погрешности и изменения размера до 1/32 (3%) по отношению к данному размеру – не имеют значения. Например, при длине дома 6 саженей царских 6х197,4см=1184,4см, выступающие части и погрешности в пределах 37 см можно не учитывать.
10. Внутренние высоты этажей и чердака делаются разными, но гармоничными друг другу саженями, могут совпадать с применёнными для наружных измерений. Если внутренних высот 3, например, 1-й, 2-й этажи и чердак, то проверка гармоничности проводится по вурфному соотношению: а-1-й этаж, b-2-й этаж, с-3-й этаж. W(a,b,с)=(а+b)(b+с)/b(a+b+с)=1.3-1.33 Проверка наружных размеров по вурфному соотношению не производится.
11. В строениях круглых (шести-восьми-многогранных) – саженью меряется диаметр (окружности, в которую вписан многогранник). И высота, конечно.
12. Если свесы крыши до 30 см, размер берётся по свесам крыши. Если более 30 см, используются 2 разные сажени - одной измеряются стены, второй полная ширина (длина) вместе со свесами.
13. Вообще, абсолютно во всех не указанных выше вариантах нужно всё измерять в саженях, метром пользоваться только для удобства перенесения саженных размеров в реальность. Это касается дверей, окон, расстояний между окнами, толщины стен.
14. Двери и окна по верху в пределах одного помещения должны быть на одном уровне.
Теперь подробно о вычислении гармоничных друг другу саженей.
Вот весь список восстановленных древнерусских саженей:
1-я группа:
1 Пилецкого 205,5 см
2 Египетская 166,3 см
3 Меньшая 134,5 см
2-я группа:
4 Казенная 217,6 см
5 Народная 176,0 см
6 Малая 142,4 см
3-я группа:
7 Греческая 230,4 см
8 Церковная 186,4 см
9 Простая 150,8 см
4-я группа:
10 Великая 244,0 см
11 Царская 197,4 см
12 Кладочная 159,7 см
5-я группа:
13 Большая 258,4 см
14 Фараона 209,1 см
15 Черняева 169,1 см
Без группы:
16 Городовая 284,8 см (равна удвоенной малой 2х142,4см)
Основные правила пользования саженями:
1. Сажени, находящиеся в одной группе (всего 5 групп по 3 сажени), друг другу негармоничны, и использовать их вместе нельзя. То есть при определении тройки высота-ширина-длина не допустимы даже 2 сажени из одной группы. Либо, если любой размер измеряется более чем одной саженью одновременно (например, высоты дома на склоне), также нужно брать сажени из разных групп.
2. Сажень Городовая как самостоятельная при строительстве домов не используется.
3. Сажень церковную не рекомендуется использовать в жилом строительстве.
4. Если расположить сажени по возрастанию длины, то они группируются в 3 ряда по 5 шт:
малые сажени: меньшая, малая, простая, кладочная, черняева;
средние сажени: египетская, народная, церковная, царская, фараона;
большие сажени: пилецкого, казённая, греческая, великая, большая.
Это как раз сначала первые в каждой из 5 групп, потом вторые и третьи. Сажени в одном ряду гармоничны друг другу, и пользоваться ими можно без ограничений.
Пользуясь этими правилами, уже можно вычислять гармоничные сочетания пропорций. Но этих сочетаний часто бывает недостаточно, и тут на помощь приходит Русский Всемер – тот самый восстановленный соизмерительный инструмент новгородского зодчего.
Конструкция и методика изготовления Русского всемера.
Русский всемер представляет собой деревянный брусок сечением 20х40 – 35х70мм и длиной в городовую сажень – 2848мм.
Тогда один из вертикальных столбцов имел бы такой «красивый» вид:
…0,25; 0,5; 1; 2; 4; 8; 16; 32; 64; 128; 256; 512; 1024…
И можно было б выбрать очень похожий набор саженей, в том же диапазоне. Они выделены жирным.
Разгадка в том, что матрицы такой в Древней Руси не знали, и более логично им было выбрать соответствие саженей размерам человека. Если принять народную сажень равной росту зодчего, то каждый мог пропорционально ей вычислить остальные сажени. Делалось это разными очень простыми методами, вообще без применения цифр и вычислений (геометрически). Несколько таких методов можно найти в источниках (ссылки в конце статьи). Ну а нам ближе цифры, будем опираться на них.
Видимо, со временем для удобства приняли единую саженную систему, ориентированную на рост среднего человека – 176см, ему приравняли сажень народную. Вот только как хранили этот «эталон», пока неизвестно. Не исключено, что это была одна их царских реликвий в виде жезла или трости. Чтобы не наломать дров, пока и мы будем опираться на этот «саженный стандарт».
Система русских саженей – наследие древней цивилизации, развивавшейся по принципам взаимосвязи всего вокруг. Нам, потомкам технократической цивилизации, потерявшим связь с Природой, невозможно понять суть и смысл тонких процессов, происходящих во Вселенной, а также устройства её самой. Мы привыкли всё делить на составляющие, разбирать, чтобы понять устройство. А нужно наоборот объединять, чтобы понять целое, создать гармонию. Система русских саженей позволяет вычислять гармоничные для Природы пропорции и творить гармонию, не вникая в процесс пропорционирования по Золотой пропорции. На данный момент восстановлены не все принципы строительства по саженям. Но того, что уже есть, вполне достаточно для сооружения несложных строений.
Итак, общие правила применения русских саженей (в основном касаемо строительства домов):
1. Делить сажень и получающиеся доли для вычисления более мелких размеров можно только на 2. При строительстве домов минимальная доля – 1/32 – вершок. Дальше сажень не делится. Вершок можно делить на любое число. Если делать в саженях мелкие предметы, можно делить на 2 до бесконечности.
2. Любой объект проектировался с использованием минимум 3-х разных гармонично связанных саженей: отдельно по высоте, ширине и длине. Чаще всего их число было 5-7, то есть внутренние размеры делались по другим гармонично связанным саженям.
3. Все параметры объектов замерялись только целым, как бы квантованным, числом измерительных инструментов - саженей, локтей, вершков и т.д. Например, длина здания равнялась 12 саженям малым по 142,4 см, что в измерении метром равно 17,088 м. Ширина равна четырем полуторным простым саженям по 150,8 х 1,5 = 2,262х4 м, а в измерении метром 9,048 м. Наконец, высота равна двум простым саженям по 150,8 см или 3,016 м. Таким образом, параметры объектов, отмеренные целым числом саженей, всегда оказываются дробными при измерении стандартным метром. Эта особенность систематически фиксируется при замерах метром всех древнеегипетских сооружений. А потому можно повториться, что достигнуть понимания структуры полуразрушенных пирамид без знания гармонии измерительных инструментов, их породивших, невозможно.
4. Допустимо вводить коэффициенты 1,5; 2; 2,5 к значению сажени, и измерять все оси соответственно полуторными, двойными, двух с половинными саженями, но этот метод не применяется в жилом строительстве.
5. При строительстве жилых зданий по всем осям снаружи берётся четное целое количество саженей, для сакральных сооружений (храмы, часовни, церкви, гробницы) нечетное, и желательно кратное 7 или 11.
6. Внутри зданий допустимо мерить дробными частями саженей, соответственно чётным или нечётным количеством.
7. Сначала подбирается высота, потом гармоничная ей ширина, потом гармоничная высоте и ширине длина (о методах подбора ниже).
8. Все размеры измеряются по выступающим частям: пристройка, ступени, козырёк, водосточная система, крест на храме, флюгер на крыше и т.д. – всё учитывается. Высота определяется по самой высокой точке дома, например конёк, а если в торце конька сооружён петух, - то по нему. Если к дому примыкает башня, высота которой превышает высоту дома, то высота Творения определяется по самой верхней точке башни. Дымоходы и вентиляционные трубы в расчёт не принимаются.
Если цоколь более 20 см, то высота меряется 2-мя разными саженями: отдельно от цоколя и отдельно от земли. Если дом на склоне, то с обоих сторон высота меряется по разным саженям. Если перепад высот менее 3%-не обращать внимания. Внутренняя высота меряется от чистового пола до потолка. При наклонном потолке-до наивысшей точки.
Длину ската крыши также лучше сделать по сажени. На изменения в расчетах она не влияет. Но при вылете свеса кровли более чем на 1/3 от высоты здания, ширину здания уже нужно мерить по ширине свесов, а также учитывать по сажени расстояние от свеса до земли (нулевой отметки здания, фундамента или цоколя).
9. Погрешности и изменения размера до 1/32 (3%) по отношению к данному размеру – не имеют значения. Например, при длине дома 6 саженей царских 6х197,4см=1184,4см, выступающие части и погрешности в пределах 37 см можно не учитывать.
10. Внутренние высоты этажей и чердака делаются разными, но гармоничными друг другу саженями, могут совпадать с применёнными для наружных измерений. Если внутренних высот 3, например, 1-й, 2-й этажи и чердак, то проверка гармоничности проводится по вурфному соотношению: а-1-й этаж, b-2-й этаж, с-3-й этаж. W(a,b,с)=(а+b)(b+с)/b(a+b+с)=1.3-1.33 Проверка наружных размеров по вурфному соотношению не производится.
11. В строениях круглых (шести-восьми-многогранных) – саженью меряется диаметр (окружности, в которую вписан многогранник). И высота, конечно.
12. Если свесы крыши до 30 см, размер берётся по свесам крыши. Если более 30 см, используются 2 разные сажени - одной измеряются стены, второй полная ширина (длина) вместе со свесами.
13. Вообще, абсолютно во всех не указанных выше вариантах нужно всё измерять в саженях, метром пользоваться только для удобства перенесения саженных размеров в реальность. Это касается дверей, окон, расстояний между окнами, толщины стен.
14. Двери и окна по верху в пределах одного помещения должны быть на одном уровне.
Теперь подробно о вычислении гармоничных друг другу саженей.
Вот весь список восстановленных древнерусских саженей:
1-я группа:
1 Пилецкого 205,5 см
2 Египетская 166,3 см
3 Меньшая 134,5 см
2-я группа:
4 Казенная 217,6 см
5 Народная 176,0 см
6 Малая 142,4 см
3-я группа:
7 Греческая 230,4 см
8 Церковная 186,4 см
9 Простая 150,8 см
4-я группа:
10 Великая 244,0 см
11 Царская 197,4 см
12 Кладочная 159,7 см
5-я группа:
13 Большая 258,4 см
14 Фараона 209,1 см
15 Черняева 169,1 см
Без группы:
16 Городовая 284,8 см (равна удвоенной малой 2х142,4см)
Основные правила пользования саженями:
1. Сажени, находящиеся в одной группе (всего 5 групп по 3 сажени), друг другу негармоничны, и использовать их вместе нельзя. То есть при определении тройки высота-ширина-длина не допустимы даже 2 сажени из одной группы. Либо, если любой размер измеряется более чем одной саженью одновременно (например, высоты дома на склоне), также нужно брать сажени из разных групп.
2. Сажень Городовая как самостоятельная при строительстве домов не используется.
3. Сажень церковную не рекомендуется использовать в жилом строительстве.
4. Если расположить сажени по возрастанию длины, то они группируются в 3 ряда по 5 шт:
малые сажени: меньшая, малая, простая, кладочная, черняева;
средние сажени: египетская, народная, церковная, царская, фараона;
большие сажени: пилецкого, казённая, греческая, великая, большая.
Это как раз сначала первые в каждой из 5 групп, потом вторые и третьи. Сажени в одном ряду гармоничны друг другу, и пользоваться ими можно без ограничений.
Пользуясь этими правилами, уже можно вычислять гармоничные сочетания пропорций. Но этих сочетаний часто бывает недостаточно, и тут на помощь приходит Русский Всемер – тот самый восстановленный соизмерительный инструмент новгородского зодчего.
Конструкция и методика изготовления Русского всемера.
Русский всемер представляет собой деревянный брусок сечением 20х40 – 35х70мм и длиной в городовую сажень – 2848мм.
 На рисунке представлен всемер в развёрнутом виде.
На рисунке представлен всемер в развёрнутом виде.
 А это увеличенная центральная часть.
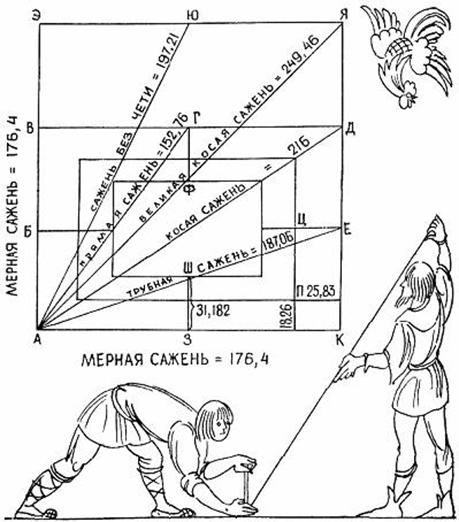
Сторона С делится на 34 равные части, сторона А на 48 частей, сторона Б на 39 частей. На четвёртой стороне наносятся длины всех саженей (на рисунке не хватает сажени Черняева из малого ряда - 1691мм). Длины саженей проводятся через все стороны всемера.
Поскольку мы всемером всё равно не будем пользоваться как измерительным инструментом, а лишь как соизмерительным – для поиска гармоничной пропорции, то можно для удобства уменьшить все размеры на коэффициент 2-4. Я уменьшил на 2. В итоге длина всемера вышла 1424мм, равной малой сажени. Далее выясняем длины клеток всех сторон. 1424/34=41,882мм – длина клеток по стороне С, 1424/39=36,513мм – Б; 1424/48=29,667мм – А. Не желательно откладывать длину клетки последовательно по шаблону. Будет накапливаться погрешность, которая в конце может составить треть клетки. Гораздо точнее будет прибавлять размер клетки последовательно со всеми знаками на калькуляторе, и отмечать на Всемере, не отнимая рулетки. Например, для стороны С это будет ряд 41,882; 83,76; 125,6; 167,5; 209,4; 251,3…1382,1; 1424,0 мм.
Вот фото Русского Всемера, который я сделал:
А это увеличенная центральная часть.
Сторона С делится на 34 равные части, сторона А на 48 частей, сторона Б на 39 частей. На четвёртой стороне наносятся длины всех саженей (на рисунке не хватает сажени Черняева из малого ряда - 1691мм). Длины саженей проводятся через все стороны всемера.
Поскольку мы всемером всё равно не будем пользоваться как измерительным инструментом, а лишь как соизмерительным – для поиска гармоничной пропорции, то можно для удобства уменьшить все размеры на коэффициент 2-4. Я уменьшил на 2. В итоге длина всемера вышла 1424мм, равной малой сажени. Далее выясняем длины клеток всех сторон. 1424/34=41,882мм – длина клеток по стороне С, 1424/39=36,513мм – Б; 1424/48=29,667мм – А. Не желательно откладывать длину клетки последовательно по шаблону. Будет накапливаться погрешность, которая в конце может составить треть клетки. Гораздо точнее будет прибавлять размер клетки последовательно со всеми знаками на калькуляторе, и отмечать на Всемере, не отнимая рулетки. Например, для стороны С это будет ряд 41,882; 83,76; 125,6; 167,5; 209,4; 251,3…1382,1; 1424,0 мм.
Вот фото Русского Всемера, который я сделал:




 На четвётрой грани отмечаем все 15 саженей, учитывая коэффициент (если он есть). В моём случае все сажени нужно делить на 2. Возле метки каждой сажени пишем её название и настоящую длину в метрах с точностью до 4-го знака. Метки саженей переносим на все грани. Возле названий саженей также пишем номер её группы (1-5). И любым способом обозначаем сажени, принадлежащие одному ряду (всего 3 ряда). Я соединил их дугами на сторонах В и С. На одной стороне получается запутанно – ряды пересекаются. У начала всемера надпишем буквенные обозначения сторон. Далее покрываем готовый Всемер бесцветным лаком в 2 слоя. Для разметки клеток и надписей лучше использовать простой карандаш, он самый светостойкий. Метки саженей можно цветным тёмным карандашом, чтобы отличались. Метки маркером, фломастером, шариковой ручкой исчезают со временем, особенно на солнце.
Алгоритмы подбора гармоничных саженей с помощьюРусского Всемера.
Всё начинается с выбора высоты дома. Например, у нас 2-х этажный дом с чердаком. Цоколь 0.5м, этажи по 3м (с учётом перекрытий), чердак 2.5 м. Итого выходит порядка 9 метров.
Примерно 9 метров мы можем получить несколькими способами: 4 сажени греческих 2,304х4=9,216м; 4 сажени казённых 2,176х4=8,704м; 6 саженей простых 1,508х6=9,048м; 6 саженей малых 1,424х6=8,544м; 6 саженей кладочных 1,597х6=9,582м. Вариантов много. Мы выберем 6 простых саженей (9,048м), это ближе всего к 9 метрам. И поскольку высоту без цоколя нужно мерить другой саженью, берём малую сажень (8,544м). Малая и простая сажени в одном ряду, гармонично связаны. Высота цоколя получится 9,048-8,544=0,504м. Пока всё в точку попало.
Дальше требуется подобрать ширину (меньший размер), а по ней - длину дома(больший размер).
Вот несколько алгоритмов:
1. Смотрим, в какой клетке на стороне С находится исходная сажень. Это клетка с номером D. Смотрим, какая сажень находится в клетке с номером D на стороне B. Это и будет искомая сажень.
2. Исходная сажень на стороне С в клетке D. В клетке D на стороне А находится искомая сажень.
3. Исходная сажень на стороне С в клетке D, а на стороне В в клетке F. В клетке с номером F на стороне С ищем искомую сажень.
4. Исходная сажень на стороне С в клетке D. Клетка D на стороне В соответствует клетке E на стороне А. В клетке Е на стороне С находится искомая сажень.
5. Исходная сажень на стороне А в клетке Е. В клетке Е на стороне С искомая сажень.
Список алгоритмов пока не полный, веду поиск недостающих. Поэтому для некоторых саженей нельзя подобрать гармоничные. Буду признателен за помощь, если кто знает другие алгоритмы.
Итак, простая сажень находится на стороне С ровно на границе 18 и 19 клеток. Поэтому выбираем алгоритм 3. На стороне В простая сажень попадает в 21 клетку. 21 клетка на стороне С это сажень Черняева – 1.691м. Выберем ширину в 4 сажени Черняева 4х1,691=6,764м.
Ищем сажень длины. По алгоритму 3 сажени черняева соответствует царская сажень 1,974м. А по алгоритму 4 получается казённая сажень, но она в одной группе с малой саженью, которой измерена высота без цоколя. Значит, казённую сажень применять нельзя. Оставляем для длины царскую сажень, берём 6 саженей. Итого 6х1,974=11,844м – длина нашего дома.
Для измерения наружных размеров мы подобрали 4 сажени: малую, простую, черняева, царскую. Все они из разных групп, главное правило соблюдено.
Особенности пропорционирования земельных участков.
Ещё не так давно по всей России замерялась земля не метром, а саженями. Существовал квадратный сажень, нечто большее, чем квадратный метр. Существовала десятна, равная 109 соткам, или 10900 квадратных метров. Есть сведения, что в десятине укладывалось 2400 квадратных саженей.
Исходя из этих сведений, узнаем размер квадратной сажени.
10900: 2400 =4,542 – точнее 4,548 кв.м.
Следует иметь в виду, что длина и ширина земельного участка замеряется различными саженями. Исходя их этого, определим, какие сажени участвовали в образовании квадратного саженя. Для этого разделим квадратный сажень последовательно на все сажени, начиная с больших. Итак:
Таблица определения участия саженей в образовании квадратного саженя
На четвётрой грани отмечаем все 15 саженей, учитывая коэффициент (если он есть). В моём случае все сажени нужно делить на 2. Возле метки каждой сажени пишем её название и настоящую длину в метрах с точностью до 4-го знака. Метки саженей переносим на все грани. Возле названий саженей также пишем номер её группы (1-5). И любым способом обозначаем сажени, принадлежащие одному ряду (всего 3 ряда). Я соединил их дугами на сторонах В и С. На одной стороне получается запутанно – ряды пересекаются. У начала всемера надпишем буквенные обозначения сторон. Далее покрываем готовый Всемер бесцветным лаком в 2 слоя. Для разметки клеток и надписей лучше использовать простой карандаш, он самый светостойкий. Метки саженей можно цветным тёмным карандашом, чтобы отличались. Метки маркером, фломастером, шариковой ручкой исчезают со временем, особенно на солнце.
Алгоритмы подбора гармоничных саженей с помощьюРусского Всемера.
Всё начинается с выбора высоты дома. Например, у нас 2-х этажный дом с чердаком. Цоколь 0.5м, этажи по 3м (с учётом перекрытий), чердак 2.5 м. Итого выходит порядка 9 метров.
Примерно 9 метров мы можем получить несколькими способами: 4 сажени греческих 2,304х4=9,216м; 4 сажени казённых 2,176х4=8,704м; 6 саженей простых 1,508х6=9,048м; 6 саженей малых 1,424х6=8,544м; 6 саженей кладочных 1,597х6=9,582м. Вариантов много. Мы выберем 6 простых саженей (9,048м), это ближе всего к 9 метрам. И поскольку высоту без цоколя нужно мерить другой саженью, берём малую сажень (8,544м). Малая и простая сажени в одном ряду, гармонично связаны. Высота цоколя получится 9,048-8,544=0,504м. Пока всё в точку попало.
Дальше требуется подобрать ширину (меньший размер), а по ней - длину дома(больший размер).
Вот несколько алгоритмов:
1. Смотрим, в какой клетке на стороне С находится исходная сажень. Это клетка с номером D. Смотрим, какая сажень находится в клетке с номером D на стороне B. Это и будет искомая сажень.
2. Исходная сажень на стороне С в клетке D. В клетке D на стороне А находится искомая сажень.
3. Исходная сажень на стороне С в клетке D, а на стороне В в клетке F. В клетке с номером F на стороне С ищем искомую сажень.
4. Исходная сажень на стороне С в клетке D. Клетка D на стороне В соответствует клетке E на стороне А. В клетке Е на стороне С находится искомая сажень.
5. Исходная сажень на стороне А в клетке Е. В клетке Е на стороне С искомая сажень.
Список алгоритмов пока не полный, веду поиск недостающих. Поэтому для некоторых саженей нельзя подобрать гармоничные. Буду признателен за помощь, если кто знает другие алгоритмы.
Итак, простая сажень находится на стороне С ровно на границе 18 и 19 клеток. Поэтому выбираем алгоритм 3. На стороне В простая сажень попадает в 21 клетку. 21 клетка на стороне С это сажень Черняева – 1.691м. Выберем ширину в 4 сажени Черняева 4х1,691=6,764м.
Ищем сажень длины. По алгоритму 3 сажени черняева соответствует царская сажень 1,974м. А по алгоритму 4 получается казённая сажень, но она в одной группе с малой саженью, которой измерена высота без цоколя. Значит, казённую сажень применять нельзя. Оставляем для длины царскую сажень, берём 6 саженей. Итого 6х1,974=11,844м – длина нашего дома.
Для измерения наружных размеров мы подобрали 4 сажени: малую, простую, черняева, царскую. Все они из разных групп, главное правило соблюдено.
Особенности пропорционирования земельных участков.
Ещё не так давно по всей России замерялась земля не метром, а саженями. Существовал квадратный сажень, нечто большее, чем квадратный метр. Существовала десятна, равная 109 соткам, или 10900 квадратных метров. Есть сведения, что в десятине укладывалось 2400 квадратных саженей.
Исходя из этих сведений, узнаем размер квадратной сажени.
10900: 2400 =4,542 – точнее 4,548 кв.м.
Следует иметь в виду, что длина и ширина земельного участка замеряется различными саженями. Исходя их этого, определим, какие сажени участвовали в образовании квадратного саженя. Для этого разделим квадратный сажень последовательно на все сажени, начиная с больших. Итак:
Таблица определения участия саженей в образовании квадратного саженя
 Как видим квадратный сажень можно измерять пятью разными парами саженей. Простая сажень участвует одна но в образовании половины квадратного саженя.
Полученные сажени рекомендуем использовать при пропорционировании и определении размеров выделенных земельных участков следующим образом:
Ширина Длина
Городовая Кладочная
Большая Народная
Великая Церковная
Греческая Царская
Казённая Фараона
Полученный размер квадратного саженя и сама десятина обладают Золотосечённой, причём наиболее точной святостью, "сакральностью", для тех жителей Земли, которые её обрабатывают. Следует ожидать, что участки, размеренные квадратной саженью будут давать больший урожай, чем размеренные метром, ибо они формируют пространство объёма урожая. Примеры повышения урожая уже отмечены в поселениях Кировской и Красноярской областей.
Автор: Андрей Кравчик.
Как видим квадратный сажень можно измерять пятью разными парами саженей. Простая сажень участвует одна но в образовании половины квадратного саженя.
Полученные сажени рекомендуем использовать при пропорционировании и определении размеров выделенных земельных участков следующим образом:
Ширина Длина
Городовая Кладочная
Большая Народная
Великая Церковная
Греческая Царская
Казённая Фараона
Полученный размер квадратного саженя и сама десятина обладают Золотосечённой, причём наиболее точной святостью, "сакральностью", для тех жителей Земли, которые её обрабатывают. Следует ожидать, что участки, размеренные квадратной саженью будут давать больший урожай, чем размеренные метром, ибо они формируют пространство объёма урожая. Примеры повышения урожая уже отмечены в поселениях Кировской и Красноярской областей.
Автор: Андрей Кравчик.


 Сакральное древней Руси... (А.Ф Черняев)
Сакральное древней Руси... (А.Ф Черняев)
|
 Все чаще и чаще в научной литературе отмечается плодотворное влияние на человека конструкций, пропорционированных по золотому сечению. Причём, имеются в виду любые конструкции и предметы, созданные человеком. От примитивной ложки до грандиозного дворца.
Становится ясно, что пропорционирование частей зданий и сооружений, соответствующее природным пропорциям и пропорциям человека, его восприятию действительности и ощущениям, является важнейшим фактором нормального функционирования человеческого организма. Но как вычислять «золотые размеры»? Из-за того, что в золотых пропорциях все числа иррациональные, вычислять их в уме или даже на калькуляторе сложно или невозможно. Тут справится только современный компьютер. Но программу для компьютера пока составить невозможно, поскольку принципы применения золотой пропорции ещё только начинают выступать из тумана. Но как выходили из ситуации наши предки? Анализ абсолютно всех древних сооружений, начиная с египетских пирамид, показывает присутствие Золотой пропорции, и многовариантность её применения сбивает с толку. А самые «свежие» из уцелевших золотосечённых сооружений – древнерусские церкви и храмы!!! Издавна и аж до 18-го века на Руси строили согласно золотым пропорциям! Только Пётр I положил конец «беспорядку», приравняв казённую сажень (217,6см) к 7 английским футам (213,360 см). В 1835г. Николай I вообще запретил остальные сажени, а в 1924 г. была введена метрическая система.
Значит, гораздо проще попробовать восстановить древнерусскую измерительную систему, чем сочинять навороченные программы для компьютера и таскать его с собой. Непонятно ещё, чем закончится такое «изобретение велосипеда».
Чтобы понять суть и смысл измерения в древнерусских саженях, придётся немного окунуться в математику и геометрию. Совсем немного, просмотрите хоть по диагонали все формулы.
Давно установлено существование загадочного «Золотого числа» Ф.
Практическое знакомство с Золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки. Из точки В восставляется перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции.
Все чаще и чаще в научной литературе отмечается плодотворное влияние на человека конструкций, пропорционированных по золотому сечению. Причём, имеются в виду любые конструкции и предметы, созданные человеком. От примитивной ложки до грандиозного дворца.
Становится ясно, что пропорционирование частей зданий и сооружений, соответствующее природным пропорциям и пропорциям человека, его восприятию действительности и ощущениям, является важнейшим фактором нормального функционирования человеческого организма. Но как вычислять «золотые размеры»? Из-за того, что в золотых пропорциях все числа иррациональные, вычислять их в уме или даже на калькуляторе сложно или невозможно. Тут справится только современный компьютер. Но программу для компьютера пока составить невозможно, поскольку принципы применения золотой пропорции ещё только начинают выступать из тумана. Но как выходили из ситуации наши предки? Анализ абсолютно всех древних сооружений, начиная с египетских пирамид, показывает присутствие Золотой пропорции, и многовариантность её применения сбивает с толку. А самые «свежие» из уцелевших золотосечённых сооружений – древнерусские церкви и храмы!!! Издавна и аж до 18-го века на Руси строили согласно золотым пропорциям! Только Пётр I положил конец «беспорядку», приравняв казённую сажень (217,6см) к 7 английским футам (213,360 см). В 1835г. Николай I вообще запретил остальные сажени, а в 1924 г. была введена метрическая система.
Значит, гораздо проще попробовать восстановить древнерусскую измерительную систему, чем сочинять навороченные программы для компьютера и таскать его с собой. Непонятно ещё, чем закончится такое «изобретение велосипеда».
Чтобы понять суть и смысл измерения в древнерусских саженях, придётся немного окунуться в математику и геометрию. Совсем немного, просмотрите хоть по диагонали все формулы.
Давно установлено существование загадочного «Золотого числа» Ф.
Практическое знакомство с Золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки. Из точки В восставляется перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции.
 Точное значение Ф находится математическим путём как корень квадратного уравнения, получаемого при делении отрезка в крайнем и среднем отношениях, то есть в соотшонении золотой пропорции:
Точное значение Ф находится математическим путём как корень квадратного уравнения, получаемого при делении отрезка в крайнем и среднем отношениях, то есть в соотшонении золотой пропорции:
 (a+c)/c=c/a=Ф Это золотая пропорция. Решений для чисел a и c бесконечное множество, и все они будут иррациональными (хотя одно число может быть и целым). А вот решение для числа Ф всего одно:
Ф=(1 + V5)/2 =1,6180339887498948482045868343656…(V5-это квадратный корень из5)
Правда, у вышеупомянутого квадратного уравнения есть ещё один корень (1- V5)/2 = - 1/Ф, но поскольку он отрицательный, а оба числа a и c у нас положительные, это решение отбрасываем.
Ф-число иррациональное бесконечное.
Обратная величина 1/Ф=0,6180339887498948482045868343656…
Квадрат Ф2= 2,6180339887498948482045868343656…
Все знаки после запятой одинаковые… Вот загадочное число, не правда ли? Но это ещё не всё.
Известный числовой ряд Фибоначчи (открыт в XIII веке), где каждый последующий член ряда равен сумме двух предыдущих, имеет вид:
1,2,3,5,8,13,21,34, 55, 89,... 377, 610,987,1598,2885,...
Нетрудно заметить, что с увеличением порядковых номеров членов деление последующего члена на предыдущий всё более приближается к золотому числу Ф:
3:2=1,5; 5:3=1,666; 21:13=1,615; 55:34=1,617;...610:377= 1,618037....
Золотое иррациональное число Ф было известно еще в Древней Греции как основа образования бесконечного ряда величин, обладающего свойствами чисел Фибоначчи, получаемых в результате умножения или деления базисной единицы 1 на золотое число Ф. Ветвь ряда, образуемая последовательным умножением на Ф, называется восходящей: 1; 1,618; 2,618; 4,236; 6,854; 11,090; 17,944; 29,034... а другая часть ряда, образуемая последовательным делением на Ф, называется нисходящей: 1; 0,618; 0,382; 0,236; 0,146; 0,090; 0,056; 0,034....
Само число 1, первые три члена восходящего ряда и семь членов ряда нисходящего составляют греческий ряд чисел, получивших название "золотая пропорция" или "золотое сечение".
Золотая пропорция — единственная геометрическая прогрессия (конечно, можно взять любое базисное число вместо 1 и будет другой ряд, но множитель 1.618… единственный), у которой есть и свойства ряда Фибоначчи: каждый последующий член ряда получается, как и числа Фибоначчи, сложением двух предыдущих членов, а весь ряд, за исключением базисной 1, состоит из иррациональных чисел. Причём, ряд бесконечен в обе стороны, в отличие от классических рядов Фибоначчи, имеющих начало.
Откуда возникли представления о делении отрезков в крайнем и среднем отношениях, позволяющем получать золотое число Ф и пропорцию, названную Леонардо да Винчи «золотым сечением», нам неизвестно.
Итак, загадочное число Ф вычислено. Но зачем оно нам понадобилось?
Оказывается, всё в природе, включая человека, создано согласно пропорциям золотого сечения.
Мы любим красоту. Наше тело интуитивно чувствует золотую пропорцию. Всё, что нам кажется красивым, обладает свойствами золотого сечения. Будь то природный ландшафт, картина художника или тело человека. Почему это так, пока однозначного ответа нет. Эзотерики сразу приводят в качестве доказательства «частоту вибраций», создаваемых разными телами, и у золотосечённых тел она вроде-бы одинаковая. Некоторые утверждают, что золотосечённые тела наоборот поглощают (или пропускают) все частоты одинаково, благодаря чему имеют сбалансированную информацию. Встречалось и такое выражение про современные простройки: «порождают стоячие волны, губительно действующие на сознание и организм человека». Учёные от науки пока совсем молчат по этому поводу.
За последние десятилетия многочисленными исследователями были установлены повсеместные проявления закона золотых пропорций от Космоса до Микромира.
Во Вселенной все известные человечеству галактики и все тела в них существуют в форме спирали, соответствующей формуле золотого сечения. Русский астроном Бутусов в 1978 г. установил, что отношение периодов обращения соседних планет вокруг Солнца равны либо золотой пропорции 1,618, либо ее квадрату 2,618.
Соотношения золотой пропорции исследователи находят в морфологической структуре растений, птиц, животных, человека.
Закономерности золотой пропорции обнаруживаются и в организации неорганической природы, например, структура талой воды, практически соответствует треугольнику золотой пропорции.
Таким образом, проявление принципа золотых пропорций наблюдается повсеместно в природе от бесконечно больших галактик до бесконечно малых клеток и атомов.
Фигура человека, исследованная немецким исследователем проф. Цейзингом в 1855 г. явилась ярким примером золотых пропорций.
Дальше придётся ещё бегло познакомиться с понятием вурфных соотношений.
Для блока, состоящего из трех элементов с длинами а, b, c вурфное отношение W(а, b, с) вычисляется по формуле:
W(a,b,с)=(а+b)(b+с)/b(a+b+с).
При этом другой блок — с другими размерами и другими соотношениями элементов — а', b', с' будет ему конформно симметричен, если величины их вурфов будут равны, т.е. если: W(a, b, с)=W(a', b',с').
Путем преобразований такие блоки могут быть совмещены один с другим с полным совпадением всех их точек.
В процессе роста размеры частей тела человека и их соотношения все время меняются. Причём, эти изменения следуют принципам конформно-симметричных преобразований. Например, если взять соотношения стопы, голени и бедра в возрасте 1 года, 10 и 20 лет, то изменения выглядят так: 1:1,27:1,40; 1:1,34:1,55; 1:1,39:1,68.
Рост различных частей тела не протекает равномерно. Голень и бедро увеличиваются значительно больше, нежели стопа, пропорции тела человека все время меняются. Вурфные же соотношения для любого возраста вычисляются с одним и тем же значением (W(1;1,27;1,40)=1,30; W(1;1,34;1,55)=1,30; W(1;1,39;1,68)=1,30) и оказываются неизменными на протяжении всего времени роста. Постоянная и неизменная величина вурфа свидетельствует о преобразовании форм нашего тела по принципам конформной симметрии. Такая же картина открывается и для других блоков: плеча — предплечья — кисти; фаланг пальцев; туловища, верхней и нижней конечностей тела и т.д.
Значения вурфов немного варьируются, составляя в среднем величину W = 1,31. В идеальном случае В.Петухов указывает W = 1,309, что при выражении через величину золотого сечения равно Ф2/2. Он называет его "золотым вурфом".
Вурфные пропорции позволяют, следовательно, выявить конформно-симметричные группы, иными словами, группы родственных отношений с единым исходным началом. Обычные двучленные пропорции показывают лишь различия, вурфные — общность некоторого множества трехчленных соотношений.
Если пропорции окружающих нас произведений архитектуры, принадлежат к случайным группам, как в большинстве современных сооружений, то человек оказывается в среде, пропорциональная структура которой по своей симметрии ему не свойственна. Такая Среда, не обладающая ни одной из характеристических групп симметрии человека, чаще всего не воспринимается им, а нередко отвергается. Вот где корень неблагоприятного психофизического воздействия Среды на человека, а не только в том, что жилые дома представляют собой набор однотипных "коробок". Тоже самое можно сказать и про притягательность и красоту любых объектов, нас окружающих.
Многие ученые уже 100 лет усердно бьются над расшифровкой и восстановлением утерянных русских саженей. Значительный прорыв произошёл после 1970г, когда в Новгороде у церкви Параскевы Пятницы был найден обломок мерила новгородского зодчего. В процессе исследований мерила сначала Пилецкому А.А., а потом Черняеву А.Ф, удалось не только восстановить его полностью, но и показать, что оно являлось одновременно измерительным и соизмерительным инструментом. На одной грани были нанесены мерки всех саженей, а остальные три грани в комплексе с первой представляли собой своеобразную логарифмическую линейку, позволяющую очень просто подбирать золотые пропорции! Заодно были вычислены недостающие сажени и уточнены размеры известных. Список саженей приведён ниже. Многие названия восстановить не удалось, многие имели по нескольку названий, поэтому придуманы новые или использовано одно из старых названий.
Также существовали более мелкие измерительные величины: полсажени (1/2 сажени), локоть (1/4 сажени), пядь (1/8 сажени), пясть (1/16 сажени), вершок (1/32 сажени). На основе саженей и их долей, а также последовательным умножением на 2 всех саженей, составлена матрица, названная «Русский Всемер»:
(a+c)/c=c/a=Ф Это золотая пропорция. Решений для чисел a и c бесконечное множество, и все они будут иррациональными (хотя одно число может быть и целым). А вот решение для числа Ф всего одно:
Ф=(1 + V5)/2 =1,6180339887498948482045868343656…(V5-это квадратный корень из5)
Правда, у вышеупомянутого квадратного уравнения есть ещё один корень (1- V5)/2 = - 1/Ф, но поскольку он отрицательный, а оба числа a и c у нас положительные, это решение отбрасываем.
Ф-число иррациональное бесконечное.
Обратная величина 1/Ф=0,6180339887498948482045868343656…
Квадрат Ф2= 2,6180339887498948482045868343656…
Все знаки после запятой одинаковые… Вот загадочное число, не правда ли? Но это ещё не всё.
Известный числовой ряд Фибоначчи (открыт в XIII веке), где каждый последующий член ряда равен сумме двух предыдущих, имеет вид:
1,2,3,5,8,13,21,34, 55, 89,... 377, 610,987,1598,2885,...
Нетрудно заметить, что с увеличением порядковых номеров членов деление последующего члена на предыдущий всё более приближается к золотому числу Ф:
3:2=1,5; 5:3=1,666; 21:13=1,615; 55:34=1,617;...610:377= 1,618037....
Золотое иррациональное число Ф было известно еще в Древней Греции как основа образования бесконечного ряда величин, обладающего свойствами чисел Фибоначчи, получаемых в результате умножения или деления базисной единицы 1 на золотое число Ф. Ветвь ряда, образуемая последовательным умножением на Ф, называется восходящей: 1; 1,618; 2,618; 4,236; 6,854; 11,090; 17,944; 29,034... а другая часть ряда, образуемая последовательным делением на Ф, называется нисходящей: 1; 0,618; 0,382; 0,236; 0,146; 0,090; 0,056; 0,034....
Само число 1, первые три члена восходящего ряда и семь членов ряда нисходящего составляют греческий ряд чисел, получивших название "золотая пропорция" или "золотое сечение".
Золотая пропорция — единственная геометрическая прогрессия (конечно, можно взять любое базисное число вместо 1 и будет другой ряд, но множитель 1.618… единственный), у которой есть и свойства ряда Фибоначчи: каждый последующий член ряда получается, как и числа Фибоначчи, сложением двух предыдущих членов, а весь ряд, за исключением базисной 1, состоит из иррациональных чисел. Причём, ряд бесконечен в обе стороны, в отличие от классических рядов Фибоначчи, имеющих начало.
Откуда возникли представления о делении отрезков в крайнем и среднем отношениях, позволяющем получать золотое число Ф и пропорцию, названную Леонардо да Винчи «золотым сечением», нам неизвестно.
Итак, загадочное число Ф вычислено. Но зачем оно нам понадобилось?
Оказывается, всё в природе, включая человека, создано согласно пропорциям золотого сечения.
Мы любим красоту. Наше тело интуитивно чувствует золотую пропорцию. Всё, что нам кажется красивым, обладает свойствами золотого сечения. Будь то природный ландшафт, картина художника или тело человека. Почему это так, пока однозначного ответа нет. Эзотерики сразу приводят в качестве доказательства «частоту вибраций», создаваемых разными телами, и у золотосечённых тел она вроде-бы одинаковая. Некоторые утверждают, что золотосечённые тела наоборот поглощают (или пропускают) все частоты одинаково, благодаря чему имеют сбалансированную информацию. Встречалось и такое выражение про современные простройки: «порождают стоячие волны, губительно действующие на сознание и организм человека». Учёные от науки пока совсем молчат по этому поводу.
За последние десятилетия многочисленными исследователями были установлены повсеместные проявления закона золотых пропорций от Космоса до Микромира.
Во Вселенной все известные человечеству галактики и все тела в них существуют в форме спирали, соответствующей формуле золотого сечения. Русский астроном Бутусов в 1978 г. установил, что отношение периодов обращения соседних планет вокруг Солнца равны либо золотой пропорции 1,618, либо ее квадрату 2,618.
Соотношения золотой пропорции исследователи находят в морфологической структуре растений, птиц, животных, человека.
Закономерности золотой пропорции обнаруживаются и в организации неорганической природы, например, структура талой воды, практически соответствует треугольнику золотой пропорции.
Таким образом, проявление принципа золотых пропорций наблюдается повсеместно в природе от бесконечно больших галактик до бесконечно малых клеток и атомов.
Фигура человека, исследованная немецким исследователем проф. Цейзингом в 1855 г. явилась ярким примером золотых пропорций.
Дальше придётся ещё бегло познакомиться с понятием вурфных соотношений.
Для блока, состоящего из трех элементов с длинами а, b, c вурфное отношение W(а, b, с) вычисляется по формуле:
W(a,b,с)=(а+b)(b+с)/b(a+b+с).
При этом другой блок — с другими размерами и другими соотношениями элементов — а', b', с' будет ему конформно симметричен, если величины их вурфов будут равны, т.е. если: W(a, b, с)=W(a', b',с').
Путем преобразований такие блоки могут быть совмещены один с другим с полным совпадением всех их точек.
В процессе роста размеры частей тела человека и их соотношения все время меняются. Причём, эти изменения следуют принципам конформно-симметричных преобразований. Например, если взять соотношения стопы, голени и бедра в возрасте 1 года, 10 и 20 лет, то изменения выглядят так: 1:1,27:1,40; 1:1,34:1,55; 1:1,39:1,68.
Рост различных частей тела не протекает равномерно. Голень и бедро увеличиваются значительно больше, нежели стопа, пропорции тела человека все время меняются. Вурфные же соотношения для любого возраста вычисляются с одним и тем же значением (W(1;1,27;1,40)=1,30; W(1;1,34;1,55)=1,30; W(1;1,39;1,68)=1,30) и оказываются неизменными на протяжении всего времени роста. Постоянная и неизменная величина вурфа свидетельствует о преобразовании форм нашего тела по принципам конформной симметрии. Такая же картина открывается и для других блоков: плеча — предплечья — кисти; фаланг пальцев; туловища, верхней и нижней конечностей тела и т.д.
Значения вурфов немного варьируются, составляя в среднем величину W = 1,31. В идеальном случае В.Петухов указывает W = 1,309, что при выражении через величину золотого сечения равно Ф2/2. Он называет его "золотым вурфом".
Вурфные пропорции позволяют, следовательно, выявить конформно-симметричные группы, иными словами, группы родственных отношений с единым исходным началом. Обычные двучленные пропорции показывают лишь различия, вурфные — общность некоторого множества трехчленных соотношений.
Если пропорции окружающих нас произведений архитектуры, принадлежат к случайным группам, как в большинстве современных сооружений, то человек оказывается в среде, пропорциональная структура которой по своей симметрии ему не свойственна. Такая Среда, не обладающая ни одной из характеристических групп симметрии человека, чаще всего не воспринимается им, а нередко отвергается. Вот где корень неблагоприятного психофизического воздействия Среды на человека, а не только в том, что жилые дома представляют собой набор однотипных "коробок". Тоже самое можно сказать и про притягательность и красоту любых объектов, нас окружающих.
Многие ученые уже 100 лет усердно бьются над расшифровкой и восстановлением утерянных русских саженей. Значительный прорыв произошёл после 1970г, когда в Новгороде у церкви Параскевы Пятницы был найден обломок мерила новгородского зодчего. В процессе исследований мерила сначала Пилецкому А.А., а потом Черняеву А.Ф, удалось не только восстановить его полностью, но и показать, что оно являлось одновременно измерительным и соизмерительным инструментом. На одной грани были нанесены мерки всех саженей, а остальные три грани в комплексе с первой представляли собой своеобразную логарифмическую линейку, позволяющую очень просто подбирать золотые пропорции! Заодно были вычислены недостающие сажени и уточнены размеры известных. Список саженей приведён ниже. Многие названия восстановить не удалось, многие имели по нескольку названий, поэтому придуманы новые или использовано одно из старых названий.
Также существовали более мелкие измерительные величины: полсажени (1/2 сажени), локоть (1/4 сажени), пядь (1/8 сажени), пясть (1/16 сажени), вершок (1/32 сажени). На основе саженей и их долей, а также последовательным умножением на 2 всех саженей, составлена матрица, названная «Русский Всемер»:
 Размеры всех саженей даны в см, выделены красным. Вверху таблицы-названия саженей. Оказалось, что все диагонали слева направо снизу вверх представляют собой ряды Фибоначчи и Золотую пропорцию одновременно. Для примера возьмём диагональ Народной сажени:
67,2+108,8=176,0; 176/108,8=1,618; 108,8/67,2=1,618.
По строкам коэффициент везде 2/Ф = 2/1,618 = 1,236.
Если расположить сажени в порядке возрастания длины, то соседние будут относиться друг к другу с одинаковым коэффициентом 1,059… – так же, как частоты соседних полутонов в музыкальном ряду.
Идея! Поскольку сажени соотносятся между собой так же, как частоты нот, можно попробовать «проиграть» проект дома, предварительно согласовав таблицу саженей с нотами, а размеры дома с длительностью нот. Возможно, дом с гармоничными размерами будет «звучать» приятно. Музыканты, проверяйте!
Матрица может быть продолжена до бесконечности во все стороны - влево и вправо, вверх и вниз.
Легко заметить, что более логичной (с нашей точки зрения) выглядела бы матрица, содержащая диагональ греческого ряда, золотую пропорцию:
…0,382; 0,618; 1; 1,618; 2,618; 11,090; 17,944; 29,034 …122,97; 198,96…
Размеры всех саженей даны в см, выделены красным. Вверху таблицы-названия саженей. Оказалось, что все диагонали слева направо снизу вверх представляют собой ряды Фибоначчи и Золотую пропорцию одновременно. Для примера возьмём диагональ Народной сажени:
67,2+108,8=176,0; 176/108,8=1,618; 108,8/67,2=1,618.
По строкам коэффициент везде 2/Ф = 2/1,618 = 1,236.
Если расположить сажени в порядке возрастания длины, то соседние будут относиться друг к другу с одинаковым коэффициентом 1,059… – так же, как частоты соседних полутонов в музыкальном ряду.
Идея! Поскольку сажени соотносятся между собой так же, как частоты нот, можно попробовать «проиграть» проект дома, предварительно согласовав таблицу саженей с нотами, а размеры дома с длительностью нот. Возможно, дом с гармоничными размерами будет «звучать» приятно. Музыканты, проверяйте!
Матрица может быть продолжена до бесконечности во все стороны - влево и вправо, вверх и вниз.
Легко заметить, что более логичной (с нашей точки зрения) выглядела бы матрица, содержащая диагональ греческого ряда, золотую пропорцию:
…0,382; 0,618; 1; 1,618; 2,618; 11,090; 17,944; 29,034 …122,97; 198,96…
 Тогда один из вертикальных столбцов имел бы такой «красивый» вид:
…0,25; 0,5; 1; 2; 4; 8; 16; 32; 64; 128; 256; 512; 1024…
И можно было б выбрать очень похожий набор саженей, в том же диапазоне. Они выделены жирным.
Разгадка в том, что матрицы такой в Древней Руси не знали, и более логично им было выбрать соответствие саженей размерам человека. Если принять народную сажень равной росту зодчего, то каждый мог пропорционально ей вычислить остальные сажени. Делалось это разными очень простыми методами, вообще без применения цифр и вычислений (геометрически). Несколько таких методов можно найти в источниках (ссылки в конце статьи). Ну а нам ближе цифры, будем опираться на них.
Видимо, со временем для удобства приняли единую саженную систему, ориентированную на рост среднего человека – 176см, ему приравняли сажень народную. Вот только как хранили этот «эталон», пока неизвестно. Не исключено, что это была одна их царских реликвий в виде жезла или трости. Чтобы не наломать дров, пока и мы будем опираться на этот «саженный стандарт».
Система русских саженей – наследие древней цивилизации, развивавшейся по принципам взаимосвязи всего вокруг. Нам, потомкам технократической цивилизации, потерявшим связь с Природой, невозможно понять суть и смысл тонких процессов, происходящих во Вселенной, а также устройства её самой. Мы привыкли всё делить на составляющие, разбирать, чтобы понять устройство. А нужно наоборот объединять, чтобы понять целое, создать гармонию. Система русских саженей позволяет вычислять гармоничные для Природы пропорции и творить гармонию, не вникая в процесс пропорционирования по Золотой пропорции. На данный момент восстановлены не все принципы строительства по саженям. Но того, что уже есть, вполне достаточно для сооружения несложных строений.
Итак, общие правила применения русских саженей (в основном касаемо строительства домов):
1. Делить сажень и получающиеся доли для вычисления более мелких размеров можно только на 2. При строительстве домов минимальная доля – 1/32 – вершок. Дальше сажень не делится. Вершок можно делить на любое число. Если делать в саженях мелкие предметы, можно делить на 2 до бесконечности.
2. Любой объект проектировался с использованием минимум 3-х разных гармонично связанных саженей: отдельно по высоте, ширине и длине. Чаще всего их число было 5-7, то есть внутренние размеры делались по другим гармонично связанным саженям.
3. Все параметры объектов замерялись только целым, как бы квантованным, числом измерительных инструментов - саженей, локтей, вершков и т.д. Например, длина здания равнялась 12 саженям малым по 142,4 см, что в измерении метром равно 17,088 м. Ширина равна четырем полуторным простым саженям по 150,8 х 1,5 = 2,262х4 м, а в измерении метром 9,048 м. Наконец, высота равна двум простым саженям по 150,8 см или 3,016 м. Таким образом, параметры объектов, отмеренные целым числом саженей, всегда оказываются дробными при измерении стандартным метром. Эта особенность систематически фиксируется при замерах метром всех древнеегипетских сооружений. А потому можно повториться, что достигнуть понимания структуры полуразрушенных пирамид без знания гармонии измерительных инструментов, их породивших, невозможно.
4. Допустимо вводить коэффициенты 1,5; 2; 2,5 к значению сажени, и измерять все оси соответственно полуторными, двойными, двух с половинными саженями, но этот метод не применяется в жилом строительстве.
5. При строительстве жилых зданий по всем осям снаружи берётся четное целое количество саженей, для сакральных сооружений (храмы, часовни, церкви, гробницы) нечетное, и желательно кратное 7 или 11.
6. Внутри зданий допустимо мерить дробными частями саженей, соответственно чётным или нечётным количеством.
7. Сначала подбирается высота, потом гармоничная ей ширина, потом гармоничная высоте и ширине длина (о методах подбора ниже).
8. Все размеры измеряются по выступающим частям: пристройка, ступени, козырёк, водосточная система, крест на храме, флюгер на крыше и т.д. – всё учитывается. Высота определяется по самой высокой точке дома, например конёк, а если в торце конька сооружён петух, - то по нему. Если к дому примыкает башня, высота которой превышает высоту дома, то высота Творения определяется по самой верхней точке башни. Дымоходы и вентиляционные трубы в расчёт не принимаются.
Если цоколь более 20 см, то высота меряется 2-мя разными саженями: отдельно от цоколя и отдельно от земли. Если дом на склоне, то с обоих сторон высота меряется по разным саженям. Если перепад высот менее 3%-не обращать внимания. Внутренняя высота меряется от чистового пола до потолка. При наклонном потолке-до наивысшей точки.
Длину ската крыши также лучше сделать по сажени. На изменения в расчетах она не влияет. Но при вылете свеса кровли более чем на 1/3 от высоты здания, ширину здания уже нужно мерить по ширине свесов, а также учитывать по сажени расстояние от свеса до земли (нулевой отметки здания, фундамента или цоколя).
9. Погрешности и изменения размера до 1/32 (3%) по отношению к данному размеру – не имеют значения. Например, при длине дома 6 саженей царских 6х197,4см=1184,4см, выступающие части и погрешности в пределах 37 см можно не учитывать.
10. Внутренние высоты этажей и чердака делаются разными, но гармоничными друг другу саженями, могут совпадать с применёнными для наружных измерений. Если внутренних высот 3, например, 1-й, 2-й этажи и чердак, то проверка гармоничности проводится по вурфному соотношению: а-1-й этаж, b-2-й этаж, с-3-й этаж. W(a,b,с)=(а+b)(b+с)/b(a+b+с)=1.3-1.33 Проверка наружных размеров по вурфному соотношению не производится.
11. В строениях круглых (шести-восьми-многогранных) – саженью меряется диаметр (окружности, в которую вписан многогранник). И высота, конечно.
12. Если свесы крыши до 30 см, размер берётся по свесам крыши. Если более 30 см, используются 2 разные сажени - одной измеряются стены, второй полная ширина (длина) вместе со свесами.
13. Вообще, абсолютно во всех не указанных выше вариантах нужно всё измерять в саженях, метром пользоваться только для удобства перенесения саженных размеров в реальность. Это касается дверей, окон, расстояний между окнами, толщины стен.
14. Двери и окна по верху в пределах одного помещения должны быть на одном уровне.
Теперь подробно о вычислении гармоничных друг другу саженей.
Вот весь список восстановленных древнерусских саженей:
1-я группа:
1 Пилецкого 205,5 см
2 Египетская 166,3 см
3 Меньшая 134,5 см
2-я группа:
4 Казенная 217,6 см
5 Народная 176,0 см
6 Малая 142,4 см
3-я группа:
7 Греческая 230,4 см
8 Церковная 186,4 см
9 Простая 150,8 см
4-я группа:
10 Великая 244,0 см
11 Царская 197,4 см
12 Кладочная 159,7 см
5-я группа:
13 Большая 258,4 см
14 Фараона 209,1 см
15 Черняева 169,1 см
Без группы:
16 Городовая 284,8 см (равна удвоенной малой 2х142,4см)
Основные правила пользования саженями:
1. Сажени, находящиеся в одной группе (всего 5 групп по 3 сажени), друг другу негармоничны, и использовать их вместе нельзя. То есть при определении тройки высота-ширина-длина не допустимы даже 2 сажени из одной группы. Либо, если любой размер измеряется более чем одной саженью одновременно (например, высоты дома на склоне), также нужно брать сажени из разных групп.
2. Сажень Городовая как самостоятельная при строительстве домов не используется.
3. Сажень церковную не рекомендуется использовать в жилом строительстве.
4. Если расположить сажени по возрастанию длины, то они группируются в 3 ряда по 5 шт:
малые сажени: меньшая, малая, простая, кладочная, черняева;
средние сажени: египетская, народная, церковная, царская, фараона;
большие сажени: пилецкого, казённая, греческая, великая, большая.
Это как раз сначала первые в каждой из 5 групп, потом вторые и третьи. Сажени в одном ряду гармоничны друг другу, и пользоваться ими можно без ограничений.
Пользуясь этими правилами, уже можно вычислять гармоничные сочетания пропорций. Но этих сочетаний часто бывает недостаточно, и тут на помощь приходит Русский Всемер – тот самый восстановленный соизмерительный инструмент новгородского зодчего.
Конструкция и методика изготовления Русского всемера.
Русский всемер представляет собой деревянный брусок сечением 20х40 – 35х70мм и длиной в городовую сажень – 2848мм.
Тогда один из вертикальных столбцов имел бы такой «красивый» вид:
…0,25; 0,5; 1; 2; 4; 8; 16; 32; 64; 128; 256; 512; 1024…
И можно было б выбрать очень похожий набор саженей, в том же диапазоне. Они выделены жирным.
Разгадка в том, что матрицы такой в Древней Руси не знали, и более логично им было выбрать соответствие саженей размерам человека. Если принять народную сажень равной росту зодчего, то каждый мог пропорционально ей вычислить остальные сажени. Делалось это разными очень простыми методами, вообще без применения цифр и вычислений (геометрически). Несколько таких методов можно найти в источниках (ссылки в конце статьи). Ну а нам ближе цифры, будем опираться на них.
Видимо, со временем для удобства приняли единую саженную систему, ориентированную на рост среднего человека – 176см, ему приравняли сажень народную. Вот только как хранили этот «эталон», пока неизвестно. Не исключено, что это была одна их царских реликвий в виде жезла или трости. Чтобы не наломать дров, пока и мы будем опираться на этот «саженный стандарт».
Система русских саженей – наследие древней цивилизации, развивавшейся по принципам взаимосвязи всего вокруг. Нам, потомкам технократической цивилизации, потерявшим связь с Природой, невозможно понять суть и смысл тонких процессов, происходящих во Вселенной, а также устройства её самой. Мы привыкли всё делить на составляющие, разбирать, чтобы понять устройство. А нужно наоборот объединять, чтобы понять целое, создать гармонию. Система русских саженей позволяет вычислять гармоничные для Природы пропорции и творить гармонию, не вникая в процесс пропорционирования по Золотой пропорции. На данный момент восстановлены не все принципы строительства по саженям. Но того, что уже есть, вполне достаточно для сооружения несложных строений.
Итак, общие правила применения русских саженей (в основном касаемо строительства домов):
1. Делить сажень и получающиеся доли для вычисления более мелких размеров можно только на 2. При строительстве домов минимальная доля – 1/32 – вершок. Дальше сажень не делится. Вершок можно делить на любое число. Если делать в саженях мелкие предметы, можно делить на 2 до бесконечности.
2. Любой объект проектировался с использованием минимум 3-х разных гармонично связанных саженей: отдельно по высоте, ширине и длине. Чаще всего их число было 5-7, то есть внутренние размеры делались по другим гармонично связанным саженям.
3. Все параметры объектов замерялись только целым, как бы квантованным, числом измерительных инструментов - саженей, локтей, вершков и т.д. Например, длина здания равнялась 12 саженям малым по 142,4 см, что в измерении метром равно 17,088 м. Ширина равна четырем полуторным простым саженям по 150,8 х 1,5 = 2,262х4 м, а в измерении метром 9,048 м. Наконец, высота равна двум простым саженям по 150,8 см или 3,016 м. Таким образом, параметры объектов, отмеренные целым числом саженей, всегда оказываются дробными при измерении стандартным метром. Эта особенность систематически фиксируется при замерах метром всех древнеегипетских сооружений. А потому можно повториться, что достигнуть понимания структуры полуразрушенных пирамид без знания гармонии измерительных инструментов, их породивших, невозможно.
4. Допустимо вводить коэффициенты 1,5; 2; 2,5 к значению сажени, и измерять все оси соответственно полуторными, двойными, двух с половинными саженями, но этот метод не применяется в жилом строительстве.
5. При строительстве жилых зданий по всем осям снаружи берётся четное целое количество саженей, для сакральных сооружений (храмы, часовни, церкви, гробницы) нечетное, и желательно кратное 7 или 11.
6. Внутри зданий допустимо мерить дробными частями саженей, соответственно чётным или нечётным количеством.
7. Сначала подбирается высота, потом гармоничная ей ширина, потом гармоничная высоте и ширине длина (о методах подбора ниже).
8. Все размеры измеряются по выступающим частям: пристройка, ступени, козырёк, водосточная система, крест на храме, флюгер на крыше и т.д. – всё учитывается. Высота определяется по самой высокой точке дома, например конёк, а если в торце конька сооружён петух, - то по нему. Если к дому примыкает башня, высота которой превышает высоту дома, то высота Творения определяется по самой верхней точке башни. Дымоходы и вентиляционные трубы в расчёт не принимаются.
Если цоколь более 20 см, то высота меряется 2-мя разными саженями: отдельно от цоколя и отдельно от земли. Если дом на склоне, то с обоих сторон высота меряется по разным саженям. Если перепад высот менее 3%-не обращать внимания. Внутренняя высота меряется от чистового пола до потолка. При наклонном потолке-до наивысшей точки.
Длину ската крыши также лучше сделать по сажени. На изменения в расчетах она не влияет. Но при вылете свеса кровли более чем на 1/3 от высоты здания, ширину здания уже нужно мерить по ширине свесов, а также учитывать по сажени расстояние от свеса до земли (нулевой отметки здания, фундамента или цоколя).
9. Погрешности и изменения размера до 1/32 (3%) по отношению к данному размеру – не имеют значения. Например, при длине дома 6 саженей царских 6х197,4см=1184,4см, выступающие части и погрешности в пределах 37 см можно не учитывать.
10. Внутренние высоты этажей и чердака делаются разными, но гармоничными друг другу саженями, могут совпадать с применёнными для наружных измерений. Если внутренних высот 3, например, 1-й, 2-й этажи и чердак, то проверка гармоничности проводится по вурфному соотношению: а-1-й этаж, b-2-й этаж, с-3-й этаж. W(a,b,с)=(а+b)(b+с)/b(a+b+с)=1.3-1.33 Проверка наружных размеров по вурфному соотношению не производится.
11. В строениях круглых (шести-восьми-многогранных) – саженью меряется диаметр (окружности, в которую вписан многогранник). И высота, конечно.
12. Если свесы крыши до 30 см, размер берётся по свесам крыши. Если более 30 см, используются 2 разные сажени - одной измеряются стены, второй полная ширина (длина) вместе со свесами.
13. Вообще, абсолютно во всех не указанных выше вариантах нужно всё измерять в саженях, метром пользоваться только для удобства перенесения саженных размеров в реальность. Это касается дверей, окон, расстояний между окнами, толщины стен.
14. Двери и окна по верху в пределах одного помещения должны быть на одном уровне.
Теперь подробно о вычислении гармоничных друг другу саженей.
Вот весь список восстановленных древнерусских саженей:
1-я группа:
1 Пилецкого 205,5 см
2 Египетская 166,3 см
3 Меньшая 134,5 см
2-я группа:
4 Казенная 217,6 см
5 Народная 176,0 см
6 Малая 142,4 см
3-я группа:
7 Греческая 230,4 см
8 Церковная 186,4 см
9 Простая 150,8 см
4-я группа:
10 Великая 244,0 см
11 Царская 197,4 см
12 Кладочная 159,7 см
5-я группа:
13 Большая 258,4 см
14 Фараона 209,1 см
15 Черняева 169,1 см
Без группы:
16 Городовая 284,8 см (равна удвоенной малой 2х142,4см)
Основные правила пользования саженями:
1. Сажени, находящиеся в одной группе (всего 5 групп по 3 сажени), друг другу негармоничны, и использовать их вместе нельзя. То есть при определении тройки высота-ширина-длина не допустимы даже 2 сажени из одной группы. Либо, если любой размер измеряется более чем одной саженью одновременно (например, высоты дома на склоне), также нужно брать сажени из разных групп.
2. Сажень Городовая как самостоятельная при строительстве домов не используется.
3. Сажень церковную не рекомендуется использовать в жилом строительстве.
4. Если расположить сажени по возрастанию длины, то они группируются в 3 ряда по 5 шт:
малые сажени: меньшая, малая, простая, кладочная, черняева;
средние сажени: египетская, народная, церковная, царская, фараона;
большие сажени: пилецкого, казённая, греческая, великая, большая.
Это как раз сначала первые в каждой из 5 групп, потом вторые и третьи. Сажени в одном ряду гармоничны друг другу, и пользоваться ими можно без ограничений.
Пользуясь этими правилами, уже можно вычислять гармоничные сочетания пропорций. Но этих сочетаний часто бывает недостаточно, и тут на помощь приходит Русский Всемер – тот самый восстановленный соизмерительный инструмент новгородского зодчего.
Конструкция и методика изготовления Русского всемера.
Русский всемер представляет собой деревянный брусок сечением 20х40 – 35х70мм и длиной в городовую сажень – 2848мм.
 На рисунке представлен всемер в развёрнутом виде.
На рисунке представлен всемер в развёрнутом виде.
 А это увеличенная центральная часть.
Сторона С делится на 34 равные части, сторона А на 48 частей, сторона Б на 39 частей. На четвёртой стороне наносятся длины всех саженей (на рисунке не хватает сажени Черняева из малого ряда - 1691мм). Длины саженей проводятся через все стороны всемера.
Поскольку мы всемером всё равно не будем пользоваться как измерительным инструментом, а лишь как соизмерительным – для поиска гармоничной пропорции, то можно для удобства уменьшить все размеры на коэффициент 2-4. Я уменьшил на 2. В итоге длина всемера вышла 1424мм, равной малой сажени. Далее выясняем длины клеток всех сторон. 1424/34=41,882мм – длина клеток по стороне С, 1424/39=36,513мм – Б; 1424/48=29,667мм – А. Не желательно откладывать длину клетки последовательно по шаблону. Будет накапливаться погрешность, которая в конце может составить треть клетки. Гораздо точнее будет прибавлять размер клетки последовательно со всеми знаками на калькуляторе, и отмечать на Всемере, не отнимая рулетки. Например, для стороны С это будет ряд 41,882; 83,76; 125,6; 167,5; 209,4; 251,3…1382,1; 1424,0 мм.
Вот фото Русского Всемера, который я сделал:
А это увеличенная центральная часть.
Сторона С делится на 34 равные части, сторона А на 48 частей, сторона Б на 39 частей. На четвёртой стороне наносятся длины всех саженей (на рисунке не хватает сажени Черняева из малого ряда - 1691мм). Длины саженей проводятся через все стороны всемера.
Поскольку мы всемером всё равно не будем пользоваться как измерительным инструментом, а лишь как соизмерительным – для поиска гармоничной пропорции, то можно для удобства уменьшить все размеры на коэффициент 2-4. Я уменьшил на 2. В итоге длина всемера вышла 1424мм, равной малой сажени. Далее выясняем длины клеток всех сторон. 1424/34=41,882мм – длина клеток по стороне С, 1424/39=36,513мм – Б; 1424/48=29,667мм – А. Не желательно откладывать длину клетки последовательно по шаблону. Будет накапливаться погрешность, которая в конце может составить треть клетки. Гораздо точнее будет прибавлять размер клетки последовательно со всеми знаками на калькуляторе, и отмечать на Всемере, не отнимая рулетки. Например, для стороны С это будет ряд 41,882; 83,76; 125,6; 167,5; 209,4; 251,3…1382,1; 1424,0 мм.
Вот фото Русского Всемера, который я сделал:




 На четвётрой грани отмечаем все 15 саженей, учитывая коэффициент (если он есть). В моём случае все сажени нужно делить на 2. Возле метки каждой сажени пишем её название и настоящую длину в метрах с точностью до 4-го знака. Метки саженей переносим на все грани. Возле названий саженей также пишем номер её группы (1-5). И любым способом обозначаем сажени, принадлежащие одному ряду (всего 3 ряда). Я соединил их дугами на сторонах В и С. На одной стороне получается запутанно – ряды пересекаются. У начала всемера надпишем буквенные обозначения сторон. Далее покрываем готовый Всемер бесцветным лаком в 2 слоя. Для разметки клеток и надписей лучше использовать простой карандаш, он самый светостойкий. Метки саженей можно цветным тёмным карандашом, чтобы отличались. Метки маркером, фломастером, шариковой ручкой исчезают со временем, особенно на солнце.
Алгоритмы подбора гармоничных саженей с помощьюРусского Всемера.
Всё начинается с выбора высоты дома. Например, у нас 2-х этажный дом с чердаком. Цоколь 0.5м, этажи по 3м (с учётом перекрытий), чердак 2.5 м. Итого выходит порядка 9 метров.
Примерно 9 метров мы можем получить несколькими способами: 4 сажени греческих 2,304х4=9,216м; 4 сажени казённых 2,176х4=8,704м; 6 саженей простых 1,508х6=9,048м; 6 саженей малых 1,424х6=8,544м; 6 саженей кладочных 1,597х6=9,582м. Вариантов много. Мы выберем 6 простых саженей (9,048м), это ближе всего к 9 метрам. И поскольку высоту без цоколя нужно мерить другой саженью, берём малую сажень (8,544м). Малая и простая сажени в одном ряду, гармонично связаны. Высота цоколя получится 9,048-8,544=0,504м. Пока всё в точку попало.
Дальше требуется подобрать ширину (меньший размер), а по ней - длину дома(больший размер).
Вот несколько алгоритмов:
1. Смотрим, в какой клетке на стороне С находится исходная сажень. Это клетка с номером D. Смотрим, какая сажень находится в клетке с номером D на стороне B. Это и будет искомая сажень.
2. Исходная сажень на стороне С в клетке D. В клетке D на стороне А находится искомая сажень.
3. Исходная сажень на стороне С в клетке D, а на стороне В в клетке F. В клетке с номером F на стороне С ищем искомую сажень.
4. Исходная сажень на стороне С в клетке D. Клетка D на стороне В соответствует клетке E на стороне А. В клетке Е на стороне С находится искомая сажень.
5. Исходная сажень на стороне А в клетке Е. В клетке Е на стороне С искомая сажень.
Список алгоритмов пока не полный, веду поиск недостающих. Поэтому для некоторых саженей нельзя подобрать гармоничные. Буду признателен за помощь, если кто знает другие алгоритмы.
Итак, простая сажень находится на стороне С ровно на границе 18 и 19 клеток. Поэтому выбираем алгоритм 3. На стороне В простая сажень попадает в 21 клетку. 21 клетка на стороне С это сажень Черняева – 1.691м. Выберем ширину в 4 сажени Черняева 4х1,691=6,764м.
Ищем сажень длины. По алгоритму 3 сажени черняева соответствует царская сажень 1,974м. А по алгоритму 4 получается казённая сажень, но она в одной группе с малой саженью, которой измерена высота без цоколя. Значит, казённую сажень применять нельзя. Оставляем для длины царскую сажень, берём 6 саженей. Итого 6х1,974=11,844м – длина нашего дома.
Для измерения наружных размеров мы подобрали 4 сажени: малую, простую, черняева, царскую. Все они из разных групп, главное правило соблюдено.
Особенности пропорционирования земельных участков.
Ещё не так давно по всей России замерялась земля не метром, а саженями. Существовал квадратный сажень, нечто большее, чем квадратный метр. Существовала десятна, равная 109 соткам, или 10900 квадратных метров. Есть сведения, что в десятине укладывалось 2400 квадратных саженей.
Исходя из этих сведений, узнаем размер квадратной сажени.
10900: 2400 =4,542 – точнее 4,548 кв.м.
Следует иметь в виду, что длина и ширина земельного участка замеряется различными саженями. Исходя их этого, определим, какие сажени участвовали в образовании квадратного саженя. Для этого разделим квадратный сажень последовательно на все сажени, начиная с больших. Итак:
Таблица определения участия саженей в образовании квадратного саженя
На четвётрой грани отмечаем все 15 саженей, учитывая коэффициент (если он есть). В моём случае все сажени нужно делить на 2. Возле метки каждой сажени пишем её название и настоящую длину в метрах с точностью до 4-го знака. Метки саженей переносим на все грани. Возле названий саженей также пишем номер её группы (1-5). И любым способом обозначаем сажени, принадлежащие одному ряду (всего 3 ряда). Я соединил их дугами на сторонах В и С. На одной стороне получается запутанно – ряды пересекаются. У начала всемера надпишем буквенные обозначения сторон. Далее покрываем готовый Всемер бесцветным лаком в 2 слоя. Для разметки клеток и надписей лучше использовать простой карандаш, он самый светостойкий. Метки саженей можно цветным тёмным карандашом, чтобы отличались. Метки маркером, фломастером, шариковой ручкой исчезают со временем, особенно на солнце.
Алгоритмы подбора гармоничных саженей с помощьюРусского Всемера.
Всё начинается с выбора высоты дома. Например, у нас 2-х этажный дом с чердаком. Цоколь 0.5м, этажи по 3м (с учётом перекрытий), чердак 2.5 м. Итого выходит порядка 9 метров.
Примерно 9 метров мы можем получить несколькими способами: 4 сажени греческих 2,304х4=9,216м; 4 сажени казённых 2,176х4=8,704м; 6 саженей простых 1,508х6=9,048м; 6 саженей малых 1,424х6=8,544м; 6 саженей кладочных 1,597х6=9,582м. Вариантов много. Мы выберем 6 простых саженей (9,048м), это ближе всего к 9 метрам. И поскольку высоту без цоколя нужно мерить другой саженью, берём малую сажень (8,544м). Малая и простая сажени в одном ряду, гармонично связаны. Высота цоколя получится 9,048-8,544=0,504м. Пока всё в точку попало.
Дальше требуется подобрать ширину (меньший размер), а по ней - длину дома(больший размер).
Вот несколько алгоритмов:
1. Смотрим, в какой клетке на стороне С находится исходная сажень. Это клетка с номером D. Смотрим, какая сажень находится в клетке с номером D на стороне B. Это и будет искомая сажень.
2. Исходная сажень на стороне С в клетке D. В клетке D на стороне А находится искомая сажень.
3. Исходная сажень на стороне С в клетке D, а на стороне В в клетке F. В клетке с номером F на стороне С ищем искомую сажень.
4. Исходная сажень на стороне С в клетке D. Клетка D на стороне В соответствует клетке E на стороне А. В клетке Е на стороне С находится искомая сажень.
5. Исходная сажень на стороне А в клетке Е. В клетке Е на стороне С искомая сажень.
Список алгоритмов пока не полный, веду поиск недостающих. Поэтому для некоторых саженей нельзя подобрать гармоничные. Буду признателен за помощь, если кто знает другие алгоритмы.
Итак, простая сажень находится на стороне С ровно на границе 18 и 19 клеток. Поэтому выбираем алгоритм 3. На стороне В простая сажень попадает в 21 клетку. 21 клетка на стороне С это сажень Черняева – 1.691м. Выберем ширину в 4 сажени Черняева 4х1,691=6,764м.
Ищем сажень длины. По алгоритму 3 сажени черняева соответствует царская сажень 1,974м. А по алгоритму 4 получается казённая сажень, но она в одной группе с малой саженью, которой измерена высота без цоколя. Значит, казённую сажень применять нельзя. Оставляем для длины царскую сажень, берём 6 саженей. Итого 6х1,974=11,844м – длина нашего дома.
Для измерения наружных размеров мы подобрали 4 сажени: малую, простую, черняева, царскую. Все они из разных групп, главное правило соблюдено.
Особенности пропорционирования земельных участков.
Ещё не так давно по всей России замерялась земля не метром, а саженями. Существовал квадратный сажень, нечто большее, чем квадратный метр. Существовала десятна, равная 109 соткам, или 10900 квадратных метров. Есть сведения, что в десятине укладывалось 2400 квадратных саженей.
Исходя из этих сведений, узнаем размер квадратной сажени.
10900: 2400 =4,542 – точнее 4,548 кв.м.
Следует иметь в виду, что длина и ширина земельного участка замеряется различными саженями. Исходя их этого, определим, какие сажени участвовали в образовании квадратного саженя. Для этого разделим квадратный сажень последовательно на все сажени, начиная с больших. Итак:
Таблица определения участия саженей в образовании квадратного саженя
 Как видим квадратный сажень можно измерять пятью разными парами саженей. Простая сажень участвует одна но в образовании половины квадратного саженя.
Полученные сажени рекомендуем использовать при пропорционировании и определении размеров выделенных земельных участков следующим образом:
Ширина Длина
Городовая Кладочная
Большая Народная
Великая Церковная
Греческая Царская
Казённая Фараона
Полученный размер квадратного саженя и сама десятина обладают Золотосечённой, причём наиболее точной святостью, "сакральностью", для тех жителей Земли, которые её обрабатывают. Следует ожидать, что участки, размеренные квадратной саженью будут давать больший урожай, чем размеренные метром, ибо они формируют пространство объёма урожая. Примеры повышения урожая уже отмечены в поселениях Кировской и Красноярской областей.
Автор: Андрей Кравчик.
Как видим квадратный сажень можно измерять пятью разными парами саженей. Простая сажень участвует одна но в образовании половины квадратного саженя.
Полученные сажени рекомендуем использовать при пропорционировании и определении размеров выделенных земельных участков следующим образом:
Ширина Длина
Городовая Кладочная
Большая Народная
Великая Церковная
Греческая Царская
Казённая Фараона
Полученный размер квадратного саженя и сама десятина обладают Золотосечённой, причём наиболее точной святостью, "сакральностью", для тех жителей Земли, которые её обрабатывают. Следует ожидать, что участки, размеренные квадратной саженью будут давать больший урожай, чем размеренные метром, ибо они формируют пространство объёма урожая. Примеры повышения урожая уже отмечены в поселениях Кировской и Красноярской областей.
Автор: Андрей Кравчик.



 Сакральное древней Руси... (А.Ф Черняев)
Сакральное древней Руси... (А.Ф Черняев)