Изменение концентрации электронов может вызываться различными причинами. Увеличение концентрации связано с процессом генерации электронов. Механизмы генерации могут быть разнообразны, но их сущность состоит в том, что электрон получает энергию, достаточную для преодоления запрещенной зоны и переходит из валентной зоны в зону проводимости. Энергия, необходимая для перехода, черпается из постороннего источника, и переход может происходить под действием света, радиации и др. В равновесном состоянии переход электронов происходит за счет тепловой энергии. В этом случае носители заряда также называются равновесными.
Изменение концентрации электронов в единицу времени определяется скоростью генерации g. Скорость генерации равна числу электронов, появляющихся в единице объема за единицу времени.
В условиях термодинамического равновесия одновременно с генерацией идет процесс рекомбинации. Скорость рекомбинации, т.е. число рекомбинировавших электрон-дырочных пар в единице объема за единицу времени, пропорциональна произведению концентраций носителей заряда. В равновесии скорость генерации равняется скорости рекомбинации.
(4.91)
Если на полупроводник действует источник генерации, то концентрации частиц будут отличаться от равновесных.
В обычных условиях протекает биполярная генерация зарядов, т.е. одновременно с рождением электрона появляется дырка. Таким образом:
(4.92)
причем 
.
При выключении источника генерации происходит уменьшение концентрации носителей зарядов, и она возвращается к равновесному значению. Очевидно, скорость уменьшения концентрации равна разности скорости рекомбинации и скорости тепловой генерации:
|
|
(4.93)
Подставим в выражение (4.93) значения неравновесной концентрации из формул (4.92) и учтем, что 
. В результате получим:
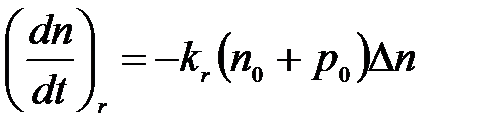(4.94)
Введем обозначение
(4.95)
Эта величина называется временем жизни неравновесных носителей заряда. Уравнение (4.94) соответственно можно переписать в виде:
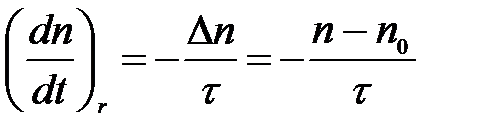(4.96)
Решение этого уравнения:
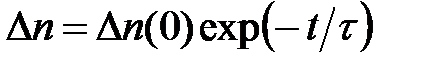(4.97)
При выключении источника генерации концентрация электронов и дырок возвращается к равновесному значению по экспоненциальному закону с характерным временем, равным времени жизни t.
Диэлектрическая релаксация. Предположим, что полупроводник помещен во внешнее электрическое поле, которое вызвало направленное движение зарядов (дрейф). Очевидно, функция распределения электронов по скоростям в этом случае отличается от равновесной функции распределения. (В направлении действия электрической силы скорость электронов в среднем больше, чем по другим направлениям). После выключения поля функция распределения трансформируется и приближается к равновесной. Это происходит по очевидной причине. Электроны, рассеиваясь в процессах взаимодействия друг с другом, с другими частицами и решеткой кристалла, "забывают" о том, что у них была направленная скорость.
После прекращения действия внешних вынуждающих факторов разность между неравновесной и равновесной функциями распределения уменьшается по экспоненциальному закону (аналогично (4.97)) с характерным временем релаксации t р. Время релаксации является характерным временем существования неравновесной функции распределения (иными словами, например, временем продолжения тока в полупроводнике после выключения напряжения).
|
|
Для установления равновесной функции распределения необходимо чтобы электрон испытал всего несколько столкновений с любыми центрами рассеяния. Для рекомбинации электрон должен встретиться с дыркой при благоприятных условиях для процесса. Поэтому время релаксации гораздо меньше времени жизни. Это приводит к тому, что свободные электроны и дырки, участвуя, например, в процессе диффузионного движения, за время жизни успевают пройти значительное расстояние от области с повышенной концентрацией.
Уравнение неразрывности. Запишем теперь уравнение неразрывности, которое является математическим выражением простого факта сохранения частиц.
Рассмотрим некоторый объем полупроводника с основаниями единичной площади и толщиной dx, через который протекает поток электронов или дырок (в принципе любых частиц). Для простоты рассмотрим одномерный случай, причем ось выберем в направлении потока.
В объеме происходит изменение числа частиц за счет их генерации, рекомбинации и вследствие того, что поток втекающих частиц может отличаеться от вытекающего потока. Поскольку разность потоков через выделенный тонкий слой dx.
(4.98)
изменение концентрации частиц, например, электронов в выделенном объеме будет:
(4.99)
Поток электронов удобнее выразить через плотность тока, умножив его на заряд электрона. Воспользовавшись также выражениями (4.84), (4.85) получим уравнение непрерывности для электронов и аналогичное выражение для дырок:
(4.100)
(4.101)
Пример использования уравнения. С помощью этих уравнений решаются многие задачи электроники. В качестве примера рассмотрим задачу о распределении неравновесных носителях заряда вдоль полупроводника, на одном конце которого внешним источником поддерживается постоянная, избыточная концентрация электронов. Будем рассматривать одномерный случай. Ось х направим вдоль полупроводника, а начало координат совместим с концом полупроводника, на котором поддерживается постоянный избыток электронов.
|
|
В стационарном случае (d / dt = 0), при отсутствии электрического поля (Е = 0) и генерации (g = 0) уравнение непрерывности (4.100) имеет вид:
(4.102)
Граничные условия выражают условия постановки задачи, а именно: в начале координат имеется постоянный избыток электронов D n (0) по сравнению с равновесным значением n 0. Далеко от начала концентрация электронов не отличается от равновесной концентрации, т.е. D n = 0
(4.103)
Решением этого уравнения будет:
(4.104)
Таким образом, концентрация избыточных зарядов (электронов) экспоненциально спадает к равновесному значению при удалении от источника неравновесности. Величина
(4.105)
имеющая размерность длины называется диффузионной длиной электронов. Она определяет характерное расстояние, на которое распространяются электроны в полупроводнике. Аналогично все делается и для дырок, для которых также существует своя диффузионная длина:
(4.106)
Вопросы и задачи для контроля усвоения
1. Как изменится концентрация электронов в собственном полупроводнике при изменении температуры с – 20оС до +40оС при ширине запрещенной зоны 0.8эВ
2. Вычислить собственные концентрации электронов в германии и кремнии при температуре Т = 300К. Эффективные массы электронов m* = 0.362 m 0 для германия и 0.595 m 0 для кремния. Ширина запрещенных зон соответственно 0.66эВ и 1.1эВ.
3. Вычислить удельные сопротивления собственных Ge и Si при 300К. Подвижности электронов и дырок: Ge m n = 3.8·103 см2В-1с-1, m p = 1.8·103 см2В-1с-1, Si m n = 3.0·103 см2В-1с-1, m p = 0.5·103 см2В-1с-1
4. Вычислить проводимость германия и кремния при добавлении 0.001% донорной примеси.
5. Найти температурный интервал, в котором концентрация электронов в кремнии постоянна. Энергетический уровень примеси лежит на 0.015эВ ниже уровня дна зоны проводимости. Считать, что концентрация не изменяется при достижении уровня 0.9 от концентрации примеси, и начинает расти при ионизации собственных атомов полупроводника на уровне 0.1 от концентрации примеси.
6. Вычислить коэффициенты диффузии электронов и дырок в германии и кремнии при температуре 300К, если подвижности Ge m n = 3.8·103 см2В-1с-1, m p = 1.8·103 см2В-1с-1, Si m n = 3.0·103 см2В-1с-1, m p = 0.5·103 см2В-1с-1
7.* Найти закон распределения концентрации электронов в полупроводнике в предположении, что на его границе поддерживается концентрация превышающая равновесную n (0) > n 0. Задачу рассмотреть в одномерном стационарном случае при отсутствии электрических полей. Указание. Воспользоваться уравнением неразрывности. Положить 
=0 (стационарность), Члены, содержащие электрическое поле отсутствуют, g = 0 (отсутствует посторонняя генерация электронов).
8. Вычислить диффузионную длину электронов в германии и кремнии, если время жизни электронов составляет 1) t n = 10-4c, 2) t n = 10-6c
Литература
1. Шалимова К.В. Физика полупроводников. М.: Энергоатомиздат, 1985, 392с.
2. Епифанов Г.И. Физика твердого тела. М.: Высшая школа. 1965. 278с.