Содержание
Введение................................................................................................................3
Критерий устойчивости Михайлова......................................................................4
Частотный критерий устойчивости Нейсквита....................................................7
Список литературы................................................................................................13
Введение
Важнейшей задачей анализа динамических систем управления является решение вопроса об их устойчивости. Техническое понятие устойчивости систем автоматического управления отражает свойство технической системы не только стабильно работать в нормальных режимах, но и "не уходить вразнос" при отклонении всевозможных параметров системы от номинала и влиянии на систему дестабилизирующих воздействий, т. е. способности системе возвращаться к равновесному состоянию, из которого она выводится возмущающими или управляющими воздействиями. Устойчивость системы - техническое требование в ряду более сложных требований, связанных с показателями качества и точности САУ.
Понятие устойчивости системы. Система находится в состоянии равновесия, если при отсутствии воздействия на систему возмущающих факторов ошибка регулирования (разность между заданным и фактическим состоянием системы) стремится к нулю. Под устойчивостью понимается способность динамической системы возвращаться в равновесное состояние после окончания действия возмущения, нарушившего это равновесие. Неустойчивая система после воздействия возмущения удаляется от равновесного состояния или начинает совершать вокруг него колебания с нарастающей амплитудой.
Критерий устойчивости Михайлова
В тридцатые годы XX в. создаются эффективные методы исследования, в частности, частотные.Появляются работы X. Найквиста (1932 г.), содержащие критерий устойчивости радиотехнических усилителей с обратной связью, и А. Михайлова (1938 г.) "Гармонический метод в теории регулирования", которые вошли в практику в послевоенные годы. В 1946 г. Г. Боде и Л. Маккол ввели логарифмическиечастотные характеристики. Г. Браун, А. Холл, Д. Кемпбелл, Г. Честнат, В. Солодовников завершили раз-работку частотных методов синтеза и расчета систем, придав им форму, удобную для инженерных расчетов.
|
|
Характерной особенностью метода является то, что об устойчивости системы судят по поведению годографа Михайлова исследуемой системы:
-
- для разомкнутой системы; -
- для замкнутой системы.
Под годографом понимается кривая, которую описывает конец вектора 
или на комплексной плоскости при измененииwот 0 до 
. Здесь 
и 
- полиномы знаменателей соответствующих передаточных функций.
На основании принципа аргумента формулируется критерий Михайлова:
Для устойчивости системы необходимо и достаточно, чтобы годограф вектора Михайлова 
для замкнутой и для разомкнутой системы) при измененииwот 0до +¥ повернулся в положительном направлении на угол(p/2)×n или, иначе, пересек по очереди n квадратов без пропусков.
Все эти годографы (и системы соответственно) устойчивы.
Эти системы неустойчивы, так как вектор годографа Михайлова вращается в отрицательном направлении.
Система неустойчива, так как квадранты проходятся непоследовательно.
Система находиться на границе устойчивости. При подсчете порядка системы каждое прохождение годографа через 0 повышает порядок на 1.
|
|
Следствие из критерия Михайлова:
Для устойчивости системы необходимо и достаточно, чтобы корни мнимой и вещественной частей годографа Михайлова перемежались.
Если корни не перемежаются, то система неустойчива.
Если характеристическое уравнение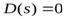 
не имеет какого либо члена, то система также неустойчива.