Процессы деятельности промышленных предприятий могут быть представлены как процессы потребления различных ресурсов. Для обеспечения своей нормальной деятельности эти структуры создают запасы ресурсов.
Запас представляет собой совокупность готовых к употреблению материальных ресурсов. Задача об установлении оптимального запаса ресурсов возникает тогда, когда размер запаса можно регулировать и когда существует, по крайней мере, одна составляющая затрат, которая меняется при изменении запаса. Например, расход денежных средств на хранение запаса определяется его количеством, расходы на перевозку грузов железной дорогой также определяются его количеством. Если завозить материальные средства на склады небольшими партиями, то хранимые запасы будут невелики, относительно небольшими будут и затраты на их хранение. Однако пополнение запасов малыми партиями приведет к увеличению числа поставок. Это потребует значительных расходов на транспортировку в связи с тем, что тариф определяется грузоподъемностью транспортного средства, а не фактической массой перевозимого груза.
Теория управления запасами занимается разработкой методов, позволяющих определить такое количество материальных средств, хранимых на складе или базе, при которых затраты денежных средств на транспортировку и хранение будут минимальными.
Классическая формулировка задачи управления запасами звучит так. Имеются некоторые запасы, затраты на содержание которых являются функцией их величины. Запасы периодически пополняются и расходуются, причем отсутствие ресурса приводит к уплате штрафа. В некоторых случаях отсутствие запасов вообще не допускается.
|
|
Ставится задача – определить такой объем разовых поставок и сроки пополнения ресурсами, при которых затраты на хранение запасов, их транспортировку и компенсацию убытков от дефицита ресурса будут минимальными.
Проблемы, связанные с определением оптимального размера партии запасов, уже достаточно давно являются предметом научного внимания. Их изучением занимаются в рамках теории производственного менеджмента, логистики, финансового менеджмента. По сути, ни один из современных учебников по финансовому менеджменту не обходит своим вниманием модель ЕОQ, рассматривая ее как важнейший инструмент управления запасами с позиции оптимизации затрат и рабочего капитала предприятия.
В экономической литературе, в том числе в области финансового менеджмента, наиболее часто базовую модель ЕOQ для детерминированных условий называют формулой Уилсона, официальная публикация модели которого состоялась в 1934 г. По другой распространенной версии автором модели ЕОQ считается американский инженер Ф. Харрис, обосновавший формулу расчета оптимального размера заказа в 1915 г. Таким образом, именно работу Харриса можно считать основополагающей. Он вывел и обосновал модель определения оптимального производственного заказа.
Критерием оптимизации в модели, так же как и во всех последующих, является минимум общих затрат на формирование и содержание запаса за планируемый период.
Модель Уилсона
Прежде всего, необходимо описать поведение выделенных затрат, поскольку оно носит разнонаправленный характер. Нахождение оптимальной величины заказа в модели Уилсона также было основано на минимизации различных видов затрат, связанных с объемом закупки:
|
|
- затрат, связанных с хранением запасов (стоимость капитала, обездвиженного в запасах; затраты на содержание товара на складе);
- затрат, связанных с выполнением заказов (затраты на ведение учетной документации; транспортные расходы на доставку заказов; затраты, связанные с размещением заказов, и т. д.). Иногда к этим видам затрат добавляют убытки, возникшие из-за дефицита запасов, расходы в виде потери части прибыли либо потери клиентов и части деловой репутации компании.
Рассмотрим логику модели Уилсона более подробно, поскольку именно она получила в научном мире наибольшее признание и считается одним из наиболее удачных вариантов развития модели Ф. Харриса. В частности, с ростом объема заказа затраты, связанные с хранением запасов, будут пропорционально возрастать, поскольку наиболее частой практикой на предприятиях является установление определенного норматива затрат на единицу материала в соответствии с их номенклатурой.
Принципиальное различие между формулами Харриса и Уилсона заключается в том, что Ф. Харрис рассматривал затраты на содержание (хранение) запаса как пропорциональные максимальному размеру текущего запаса, а Р. Уилсон – среднему размеру хранимого запаса. Отсюда в модели Уилсона появляется в числителе подкоренного выражения коэффициент 2, а получаемый при численных расчетах результат различается приблизительно в 1,4 раза
Точкой заказа называют тот уровень запасов,при котором размещаютзаказ на их пополнение.
|
|
Модель EOQ может использоваться и для определения оптимальной партии выпуска готовой продукции, позволяя минимизировать затраты на хранение запасов готовой продукции и операционные затраты, связанные с переналадкой оборудования, подготовкой производства к выпуску новой партии продукции.
Используя вместо показателя объема производственного потребления показатель планируемого объема производства продукции, можно определить оптимальный размер партии производимой продукции и оптимальный средний размер запаса готовой продукции. Модель экономичного размера заказа позволяет определить оптимальную величину партии поставки и отгрузки, но в силу жестких исходных предпосылок ее применимость на практике ограничена. В основе модели EOQ лежат следующие основные допущения:
1) весь спрос удается удовлетворить;
2) величина спроса известна и неизменна;
3) продолжительность операционного цикла известна и неизменна;
4) цена продукции постоянна;
5) горизонт планирования бесконечен;
6) не возникает никаких эффектов в связи с множественностью видов продукции;
7) отсутствуют запасы в пути;
8) капитал не ограничен.
Модель Арроу-Т. Харриса-Маршака (АНМ)
Данная модель определения оптимального объема поставки исходит из той же проблемной области, как и две предыдущих, однако вносятся некоторые уточнения:
- политика закупок определяется для каждого отдельного вида материалов;
- заранее известны поставщики и условия поставки;
- годовая потребность в материале составляет М единиц и в рассматриваемом периоде (год) распределяется равномерно, ее объем не меняется в течение неопределенного времени;
- закупка может осуществляться в любых необходимых количествах илюбой момент времени;
- известна закупочная цена единицы материала, помимо собственно цены материала в нее входят расходы на упаковку, транспортировку и прочие расходы, если их можно рассчитать на единицу закупаемого материала.
Авторы также поставили перед собой задачу найти постоянное количество материала, которое нужно приобретать через равные промежутки времени. Критерием оптимизации также служит снижение совокупных затрат, связанных с формированием запасов, однако особенностью модели является состав затрат.
В модели АНМ совокупные затраты состоят из двух частей:
- во-первых, постоянных затрат на приобретение партии kf;
- во-вторых, расходов на хранение и неполученного процента из-за замораживания капитала в материальных ресурсах на складе.
Расходы на хранение определяются как доля от стоимости материалов, находящихся на складе. Применяемый для этого коэффициент нормы расходов на хранение l показывает размер затрат на хранение товаров стоимостью в 100 у. е. в течение года. Неполученный из-за замораживания капитала процент рассчитывается с помощью заданной учетной ставки процента z. Границы решения лежат в интервале между двумя крайними ситуациями. Годовая потребность в материале покрывается за счет единовременной поставки. В этом случае постоянные издержки на приобретение возникают один раз за период, однако значительно возрастают расходы на хранение из-за увеличения запасов на складе.
Поставки осуществляются ежедневно и расходы на хранение, тем самым, минимальны. Снижение расходов на хранение компенсируется ростом постоянных издержек на приобретение, возникающих ежедневно.
Совокупные затраты, связанные с формированием запасов, определяются с помощью пяти параметров: годовой потребности в материале М, закупочной цены за единицу материала р, постоянных расходов на приобретение партии kf, нормы расходов на хранение l и ставки неполученного из-за замораживания капитала процента z.
Логика рассуждений авторов во многом повторяет логику рассуждений Р. Уилсона. Материал закупается M/x раз в год. При этом постоянные издержки на приобретение составляют – kf ∙ M/x в год. Годовые расходы на хранение и размер неполученного процента на замороженный капитал рассчитываются от средней величины складских запасов на период между поставками в объеме х. Средний уровень складских запасов равен – x /2. Стоимость хранящихся материалов, на основе которой рассчитываются расходы на хранение и неполученный процент, определяется как – x∙p /2.
Таким образом, совокупные затраты, связанные с формированием запасов, определяются следующим образом (формула 3.9):
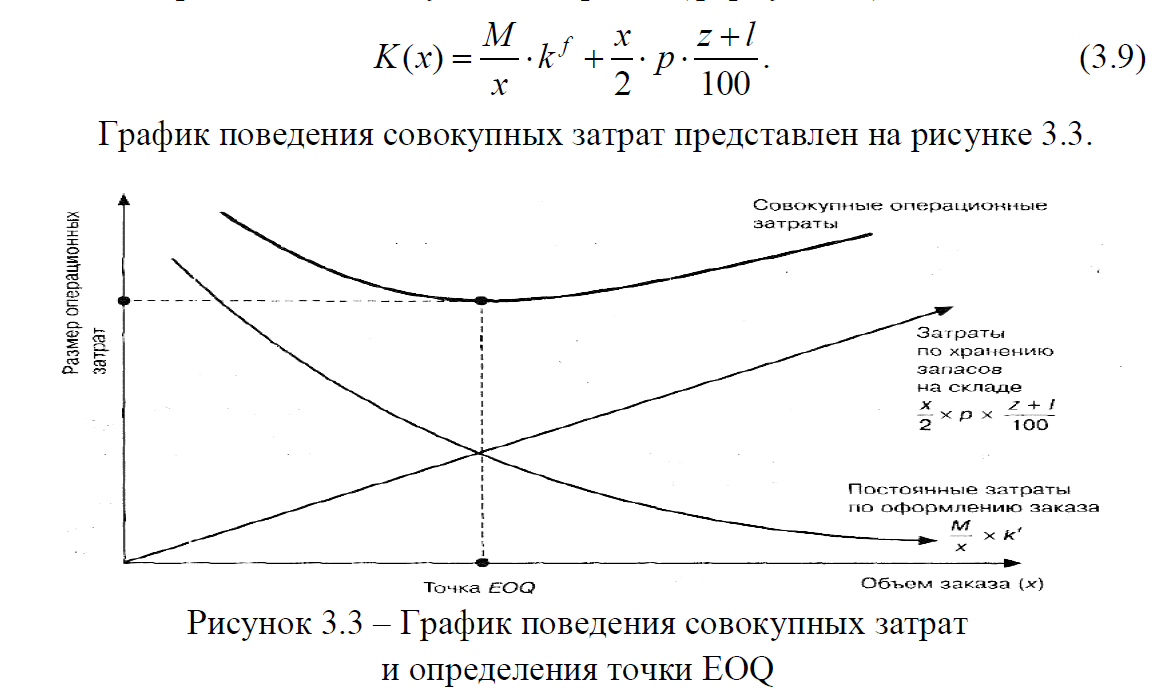
Чтобы минимизировать совокупные затраты, необходимо, так же как и в модели Уилсона, дифференцировать данное выражение по x и приравнять первую производную к нулю (формула 3.10):
Безусловным достоинством рассмотренной модели является выделение авторами ставки альтернативных затрат по хранению запасов – z. Этопозволяет существенно расширить границы применения модели и использовать ее в целях максимизации благосостояния акционеров.
В заключение отметим, что применение рассмотренных моделей требует учета ограничений, которые вводились авторами, однако это не в полной мере ограничивает области их использования. В некоторых случаях можно дополнить или видоизменить базовые версии моделей.
Однако не всякое ограничение области применения базовых моделей может быть преодолено с помощью ее видоизменения. Если объем потребности в материале не является постоянным, а характеризуется сезонными колебаниями или снижается в течение года, использование базовой модели невозможно. Во-первых, средний уровень запасов на складе между поставками уже не может определяться как половина объема единовременной поставки. Во-вторых, что более существенно, каждый раз необходимо закупать неодинаковое количество материала. Такая ситуация достаточно часто встречается в практической деятельности предприятия. Поэтому в экономической литературе стали появляться достаточно сложные, так называемые динамические модели, позволившие устранить этот серьезный недостаток.