Уравнение Клапейрона-Клаузиуса

Лабораторная работа №4

Измерение давления насыщенных паров жидкостей и растворов

Цель работы: 1) Измерить давление пара над жидким веществом.

2) Определить энтальпию испарения ацетона путем измерения давления пара при различных температурах.

Продолжительность работы: 4 ч.

Приборы и реактивы: Измеритель температуры цифровой 4-2; прибор для измерения температуры Cobra4; Cobra4 Mobile- Link; калориметр прозрачный
1200 мл; датчик температуры погружного типа Pt100; круглая колба 100 мл; безопасная бутылка 500 мл, 2 х Gl 18/8, 1 х 25/12; манометр, 0 - 1000 мбар; водоструйный насос; штатив; мерный цилиндр 50 мл; воронка; глицерин; ацетон; хлорид натрия.

Теоретические сведения

Фазовые равновесия в однокомпонентной системе

В однокомпонентной системе фазы представляют собой одно и то же вещество, находящееся в различных агрегатных или аллотропных состояниях. Если вещество образует в твердом состоянии одну кристаллическую форму, то оно может существовать лишь в трех фазах (газообразной, жидкой и одной твердой). Если же вещество может существовать в различных кристаллических модификациях (аллотропия), то каждая из модификаций будет являться фазой. Многие элементы могут образовывать различные кристаллические модификации, например, углерод, сера, фосфор, олово.

Состояние однокомпонентной системы можно описать с помощью пространственной диаграммы в координатах P - T - V: по одной из осей откладываются значения температуры, по другой - значения давления, по третьей - значения молярного объема системы. Однако трехмерные диаграммы не очень удобны для практического применения, и поэтому обычно пользуются не ими, а их проекциями на координатные плоскости - чаще всего на плоскость P - T.

Для вещества, образующего в твердом состоянии одну кристаллическую форму, например, для воды в области относительно невысоких давлений, диаграмма состояния системы имеет наиболее простой вид (рис.1).

Рис. 1 Диаграмма состояния воды

Уравнение Клапейрона-Клаузиуса

Применяя к равновесной однокомпонентной системе, состоящей из двух фаз, второй закон термодинамики, можно получить соотношение, связывающее давление и температуру.

На рис. 2 приведен фрагмент гипотетической фазовой диаграммы. Рассмотрим фазовый переход α - β. Поскольку фазы α и β находятся в равновесии друг с другом, то изменение свободной энергии Гиббса для рассматриваемого перехода равно нулю. То есть Δ G_P,T = 0 для всех точек линии, разделяющей фазы α и β.

Рис. 2 Фрагмент фазовой диаграммы однокомпонентной системы

Если параметры системы Р, Т меняются так, что равновесие в системе сохраняется, то:

d Δ G_P,T = 0. (1)

Согласно свойствам полного дифференциала функции:

(2)

Тогда выражение (1) можно переписать в виде:

(3)

Согласно известным термодинамическим соотношениям: Откуда:

(4)

Подставляя (4) в (3), получим: или

(5)

Изотермические фазовые переходы и полиморфные превращения можно считать обратимыми процессами, поэтому, в соответствии со вторым законом термодинамики:

(6)

тогда:

(7)

Уравнение (7), применимое к любому двухфазному равновесному превращению, есть не что иное как уравнение Клапейрона, записанное в дифференциальной форме. Для интегрирования уравнения Клапейрона, перепишем (7) в виде:

(8)

Интегрируя выражение (8), получаем:

(9)

Соотношения (7) и (9) справедливы для всех типов фазовых переходов. Однако для переходов твердое-газ и жидкость-газ можно сделать приближения, которые позволят получить очень важное для практического использования уравнение Клапейрона-Клаузиуса.

При равновесии двух конденсированных фаз, например твердое-жидкость или твердое-твердое, молярные объемы фаз сравнимы по величине. Но при равновесиях твердое-газ или жидкость-газ в условиях, далеких от критических, молярный объем газовой фазы намного больше молярного объема конденсированной фазы (твердой в случае возгонки и жидкой в случае испарения). Поэтому можно принять:

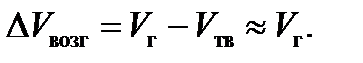
Для области относительно низкого давления (не более 5∙10⁶ Па) пар будет вести себя как идеальный газ и его состояние можно с большой степенью достоверности описать с использованием уравнения Менделеева-Клайперона:

(10)

После подстановки (10) в выражение (7) получим:

(11)

где 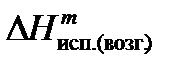- тепловой эффект испарения (возгонки) 1 моля вещества.

Это выражение является частным случаем уравнения (7) для процессов испарения и возгонки и называется уравнением Клапейрона-Клаузиуса.

Для интегрирования уравнения Клапейрона-Клаузиуса, перепишем его в виде:

или (12)

(13)

В узком интервале температур тепловой эффект фазового перехода мало зависит от температуры, поэтому можно принять = сonst.

Неопределенное интегрирование уравнения (13) дает выражение:

(14)

(15)

где const - константа интегрирования, или, если обозначить

, а , то

Согласно этим уравнениям зависимость ln P = f (1/ T) имеет линейный характер. По тангенсу угла наклона прямой, построенной в координатах ln P -1/ T, можно определить тепловой эффект испарения (возгонки) вещества.

Интегрируя уравнение (11) в пределах от P ₁ до P ₂ и от T ₁ до Т ₂, получаем:

(16)

Экспериментальная часть

На рис.3 представлен стенд для определения давления насыщенных паров жидкостей в смесях. Стенд оснащен измерительной системой Cobra4 -Mobile -Link, которая в сочетании с блоком Cobra4 -Sensor -Unit термодинамика идеально подходит для одновременного измерения давления и температуры. Cobra4 -Link представляет собой современный, мощный ручной измерительный прибор, к которому подключаются сенсорные блоки Cobra4.

Рис.3 стенд для определение давления насыщенных паров жидкостей в смесях