Методика выполнения работы. Убедитесь, что установка собрана, как показано на рис

Убедитесь, что установка собрана, как показано на рис. 3. В одну горловину круглой колбы вставлена короткая стеклянная трубка с односторонним краном и уплотнителем; в горловину номер три через защитный рукав вставлен температурный датчик типа Pt100, соединенный с цифровым измерителем температуры 4-2. В центральной горловине закреплена короткая стеклянная трубка, подключенная к адаптеру коротким силиконовым шлангом (внутр. Ø 7 мм) и далее к измерительному щупу цифрового манометра (шлангом внутр. Ø 2 мм). Используйте резиновую вакуумную трубку с односторонним запорным краном для подключения ко второй горловине «безопасной бутылки», и подсоедините их к водоструйному насосу.

Налейте несколько капель ацетона в защитный рукав в третьей горловине для улучшения теплопередачи, а затем вставьте температурный датчик типа Pt100. Заполните калориметр смесью льда и поваренной соли, и контролируйте температуру этой смеси вторым температурным зондом.

Налейте в круглую колбу 50 мл ацетона, но не погружайте ее в калориметр с морозильной смесью. Установите водяной насос в рабочее положение в колбу, до закипания ацетона. Когда это произойдет, закройте запорный кран на круглой колбе и опустите колбу в морозильную смесь. Как только температура упадет ниже -5°C, откройте запорный кран для удаления остаточного воздуха из колбы. Когда давление составит примерно 50 гПа, закрыть запорный кран и осторожно открыть трехходовой кран на «безопасной бутылке», чтобы воздух медленно уходил. Выключите насос и зафиксируйте давление в круглой колбе, с помощью цифрового манометра. В течение 10 минут, она должна подниматься максимально на 2 гПа (иначе убедитесь в герметичности подключения). Увеличивайте температуру в круглой колбе с шагом 2 – 3°C добавлением воды к морозильной смеси (смесь хорошо перемешать). После каждого повышения температуры, подождите пока восстановиться равновесное испарения и запишите температуру ацетона в колбе и соответствующее давление. Продолжать эксперимент до температуры 20°C. После этого впустить воздух в колбу, постепенно открывая запорный кран.

Теория и расчет.

Испарение (конденсация) вещества является фазовым переходом I рода. При таком переходе свойства, выражаемые первыми производными энергии Гиббса по температуре (энтропия, S), и давлению (объем, V) меняются скачком при непрерывном изменении этих р и Т.

Для процесса испарения в однокомпонентной системе, при равновесии между жидкостью (l) и паром (g), справедливо уравнение Клайперона-Клаузиуса:

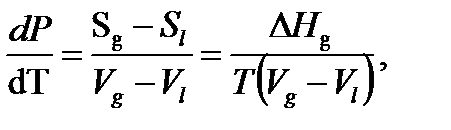(1)

где p - давление перехода, Па; 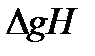- энтальпия испарения, т.е. разница между мольной энтальпией пара 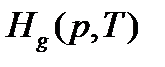и мольной энтальпией жидкости при давлении p и температуре Т. Если пренебречь мольным объемом жидкости, 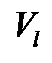, по сравнению с мольным объемом газа, , и считать пар идеальным газом (вдали от критической температуры), то можно получить уравнение (1) в виде:

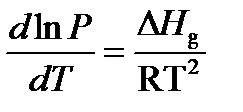(2)

После интегрирования (2) с учетом того, что 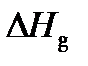в узком интервале температур остается постоянной величиной, получим:

(3)

где С – постоянная интегрирования.

Выражение (3) в координатах ln p – 1/ Т представляет собой линейную зависимость, тангенс угла наклона которой к оси абсцисс равен 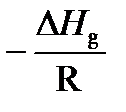. Пренебрегая зависимостью от давления, можно считать, что в уравнениях (2) и (3) 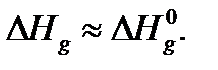Напомним, что мольная энтальпия 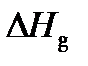идеального газа не зависит от давления при постоянной температуре. Величина 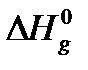называется стандартной энтальпией испарения.

С помощью уравнения (3) можно определить нормальную температуру кипения Т _н.т.к. (р = 1 атм или 760 мм.рт.ст.) и теплоту испарения 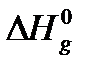, а затем значение в нормальной точке кипения жидкости.

(4)

По правилу Трутона для большинства жидкостей отношение теплоты испарения к абсолютной температуре кипения или Значения теплот и энтропий испарения некоторых жидкостей в их нормальных точках кипения представлены в таблице в приложении.

Уравнение (3) часто используется в качестве интерполяционного в следующей форме:

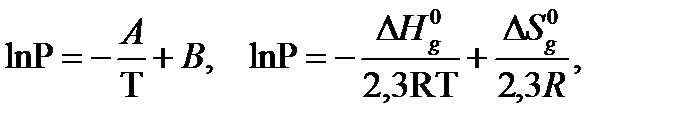(5)

где А и В – постоянные. Нормальная температура кипения Т _н.т.к. вычисляется по уравнению (5) при (р = 1 атм или 760 мм.рт.ст.):

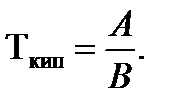(6)

Повышение температуры кипения (р = 1 атм) раствора, Δ Т, содержащего незначительное количество растворенного вещества (мольная доля x < 0,1) может описано с помощью эбуллиоскопического уравнения:

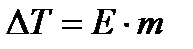, (7)

Где Е – эбуллиоскопическая константа, а m – моляльность раствора. Уравнение (7) выведено в предположении, что для растворителя выполняется закон Рауля. Величина Е равна повышению температуры кипения раствора, содержащего один моль вещества в 1000г растворителя (если при этой концентрации раствор останется идеальными):

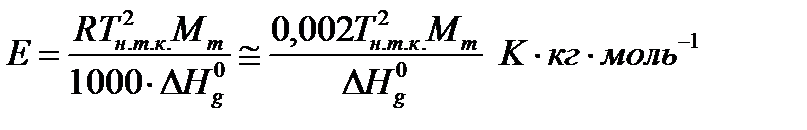(8)

Эбуллиоскопическая константа не зависит от природы растворенного вещества и характерна для данного растворителя. Величина Е велика для растворителей с высокой точкой кипения, высокой мольной массой 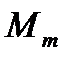, но малой теплотой испарения.

Таблица

Зависимость давление насыщенного пара от температуры

(Данные и результаты
ΔvH = 35,93 кДж моль-1 (Лит.: ΔvH (25 ° С) = 30,99 кДж моль-1);
ΔvH (56 ° C, температура кипения) = 29,10 кДж моль-1
ЛНФ?

Рис. 2: Земельный логарифма давления паров против
обратной температуры

принцип
Для каждой температуры, удельном давлении газовой фазы
жидкость устанавливает себя над жидкостью - давление пара.
Если внешнее давление понижается на отвода газа
фаза, равновесие восстанавливает себя через испарение
части жидкой фазы.
задача
Определить энтальпию испарения ацетона путем измерения
давление пара при различных температурах.

Требования к отчету

Отчет должен содержать:

1) заполненную форму таблицы;

2) графики зависимости p = f (T); ln p = f (1/ Т);

3) расчет коэффициентов А и В, энтальпии испарения, энтропии, температуры кипения жидкости, константы Трутона и эбуллиоскопической константы;

4) выводы по работе.