Основная лемма Дарбу.
 =
= 
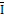 =
= 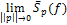
Док-во
1) f=c => ∀ p  (f)=
(f)=  (f)=c*(b-a)
(f)=c*(b-a)
2) f≠c => m<M.
Пусть ∀ ε>0 ∃  :
:  (f)-
(f)-  < ε/2;
< ε/2;  -разбиение [a,b] на L-точек включая a,b.
-разбиение [a,b] на L-точек включая a,b.
δ=ε/2L(M-m) => ( (f)-
(f)-  (f))< ε/2; (
(f))< ε/2; ( (f)-
(f)-  < ε/2;
< ε/2;
 (f)-
(f)-  =(
=( (f)-
(f)-  (f))+(
(f))+( (f)-
(f)- 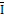 )< ε/2+ ε/2< ε.
)< ε/2+ ε/2< ε.
Основная теорема (критерий интегрируемости).
Пусть f опр. На [a,b]. След. 3 условия попарно эквивалент:
1) f интегр. На [a,b];
2) ∀ ε>0 ∃ p:  -
-  < ε;
< ε;
3)  =
= 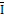 =
= 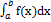 .
.
Теорема об интегрируемости по Риману непрерывной функции.
1) F непр на [a,b] => f ∈ ℛ [a,b]. (f-интегр на [a,b])
2) F интегр ó f непр.
Теорема об интегрируемости монотонной функции.
1) F монотонна на [a,b] => f ∈ ℛ [a,b].
2) F интегр ó f монотонна.
Теорема. F-огр. на [a,b] и ∀ ε>0 ∃ конечно число интервалов, покрывающих все точки
разрыва f и имеющих суммарную длину <ε => f ∈ ℛ [a,b].
Следствие 1. Если f имеет конечное число точек разрыва => f ∈ ℛ [a,b].
Следствие 2. Если f ∈ ℛ [a,b], а g опр. На [a,b] и f(x)=g(x) во всех точках [a,b]=>g∈ ℛ [a,b]
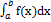 =
=  .
.
Линейность интеграла.
Пусть f,g ∈ ℛ [a,b] λ∈R => f+g, f *λ ∈ ℛ [a,b];  =
= 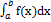 +
+ 
 = λ
= λ 
Док-во  (f+g,
(f+g,  )=
)=  (f,
(f,  )+
)+  (g,
(g,  );
);  (
(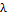 *f,
*f,  )=
)=  *
*  (f,
(f,  );
);
Аддитивность интеграла относительно пределов интегрирования.
Пусть a<b<c. Функция f интегрируема на отрезке [a,c], тогда и только тогда, когда она интегрируема на каждом из отрезков [a,b] и [b,c], при этом
 =
= 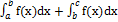
Замечание f ∈ ℛ [a,b] => |f| ∈ ℛ [a,b], но f ∈ ℛ [a,b] <  f ∈ ℛ [a,b].
f ∈ ℛ [a,b].
Монотоность интеграла: f,g ∈ ℛ [a,b], ∀ x ∈ [a,b]: f(x)<=g(x) => 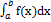 <=
<= 
Интегрируемость произведения, частного и модуля.
f,g  R[a,b]=>f*g,(f) и 1/f при |f(x)|
R[a,b]=>f*g,(f) и 1/f при |f(x)|  d>0
d>0  R[a,b]
R[a,b]
Замечание: из интегрируемости ф-ии вытекает интегрируемость модуля, но не наоборот.
Монотонность интеграла и оценка модуля интеграла.
f,g  R[a,b],
R[a,b],  x
x  [a,b] f(x)
[a,b] f(x)  g(x), тогда
g(x), тогда 
 .
.
Док-во:  P
P 
 (f,
(f,  )
) 
 (g,
(g,  .
.
Следствие: Если f  R[a,b] и
R[a,b] и 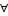 x
x  [a,b] f>0 =>
[a,b] f>0 =>  0.
0.
Оценка модуля: f  R[a,b]=> |
R[a,b]=> |  |
| 
Д-во: |f|  R[a,b],
R[a,b],
-|f(x)|  f(x)
f(x)  |f(x)|
|f(x)|
-|  |
|  .
.
Первая теорема о среднем.
Пусть f,g ∈ ℛ [a,b], g(x)>=0 ∀ x ∈ [a,b] (либо g(x)<=0)
m=inf f(x), M=sup f(x) --> ∃ ϻ ∈ [m,M]  = ϻ *
= ϻ * 
Замечание f непр. На [a,b] => ∃c ∈ [a,b] f(c) = ϻ
Непрерывность интеграла по верхнему пределу интегрирования.
Пусть f  R[a,b],=>
R[a,b],=> 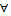 x
x  [a,b] f
[a,b] f  R[a,x]
R[a,x]
Обозначим (1) F(x)= 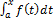 ,F(x) называют так же интегралом с переменным верхним пределом интегрирования.
,F(x) называют так же интегралом с переменным верхним пределом интегрирования.
Теорема: f  R[a,b]=>F определена равенством (1),непрерывна на [a,b].
R[a,b]=>F определена равенством (1),непрерывна на [a,b].
Д-во:Пользуясь определением пред. Коши,рассмотрим приращение ф-ии.
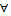 x
x  [a,b] |F(x+h)-F(x)|=|
[a,b] |F(x+h)-F(x)|=|  -
- 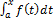 |=
|=  |
|  M|h|->0(M=supf(x)).
M|h|->0(M=supf(x)).
Т.е F(x+h)->(при h->0)F(x)=>F непрерывна в x.
Дифференцируемость интеграла по верхнему пределу интегрирования.
f  R[a,b], f непрерывна в т.
R[a,b], f непрерывна в т. 
 [a,b]=>
[a,b]=>  F’(
F’(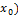 =f(
=f(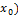 .
.
Определения несобственных интегралов двух типов.
Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий:
Предел a или b (или оба предела) являются бесконечными;
Функция f(x) имеет одну или несколько точек разрыва внутри отрезка [a, b].
Абсолютная сходимость несобственного интеграла. Признаки мажорации и сравнения.
Критерий Коши(для док-ва): 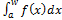 сходится ó
сходится ó 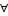
 >0
>0  B
B  [a,w):
[a,w):
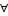
 и
и 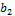
 [B,w) вып. условие:
[B,w) вып. условие:
|  | <
| <  .
.
Определение. 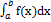 абсолютно сход <=>
абсолютно сход <=>  сход.
сход.
Теорема 2.
Если 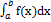 абсолютно сход =>
абсолютно сход => 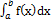 сход. (критерий Коши)
сход. (критерий Коши)
Теорема 3.
Пусть ∀ x ∈ [a,w) f(x)>=0, тогда  <=> F(t)=
<=> F(t)=  , где t∈ [a,w).
, где t∈ [a,w).
Признак мажорации
∀ x ∈ [a,w) 0<=f(x)<=g(x) и  сход =>
сход =>  сход. (теорема 3)
сход. (теорема 3)
Док-во 0<=F(t) огран <=G(x) огран =>  сход.
сход.
Признак сравнения в предельной форм
Пусть ∀ x ∈ [a,w) f(x)>=0, g(x)>0.
 =A, 0<A<+
=A, 0<A<+  =>
=> 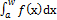 и
и  ведут себя одинаково.
ведут себя одинаково.
Определение. Несобственный интеграл назыв. услов сход, если он сход, но не сход абсолютно.
Признаки Абеля и Дирихле.
Абеля:
1)  сходится.
сходится.
2) g монотонная и ограниченна на [a,w)=> 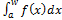 сходится.
сходится.
Дирихле:
1)F(t)=  огранич.
огранич.
2)g(x) монотонно стремится к 0 при x->w
=>  сходится
сходится
Д-во:  =g(
=g( )*
)* 