Отчет
Лабораторная работа № 1:
«Расчет статистических характеристик надёжности устройств в условиях эксплуатации»
Студент гр. 236-6:
_________ Важинский А.С.
_________ Юнусов Р.В.
«___»______________2008 г.
Руководитель:
_____________ Козлов В. Г.
«___»______________2009 г.
2009 г.
Содержание:
1 Введение. 3
2 Исключение грубых ошибок измерения. 3
2.1 Критерий Ирвина. 3
2.2 Метод трёх сигма. 4
3 Построение ряда распределения. 4
4 Построение эмпирических кривых распределения. 5
5 Выбор теоретического закона распределения. 6
5.1 Проверка закона распределения по критерию согласия Колмогорова. 6
5.2 Проверка теоретического закона распределения по критерию согласия Пирсона. 7
6 Заключение. 9
Список литературы.. 10
Приложение. 11
Введение
В данной работе била проведена статистическая обработка опытных данных, выбран соответствующий закон распределения, определяющая по внешнему виду построенных графических изображений.(кривыми распределения)
Целью данной работы является закрепление теоретических знаний по дисциплине «Теория надёжности», в том числе и приобретение навыков и освоение основных методов технических расчетов и проектирования.
2 Исключение грубых ошибок измерения
Критерий Ирвина
Для исключения грубых ошибок измерения существует большое количество методов. Один из них – метод Ирвина. Критерий Ирвина основан на оценке разности двух наибольших или наименьших членов выборки.
Определяется величина 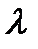 , равная [1]
, равная [1]
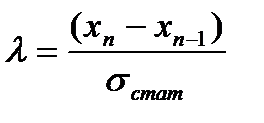 , (2.1)
, (2.1)
где 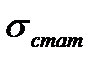 - статистическая оценка среднеквадратичного отклонения от среднего арифметического значения и находится по формуле (2.2)
- статистическая оценка среднеквадратичного отклонения от среднего арифметического значения и находится по формуле (2.2)
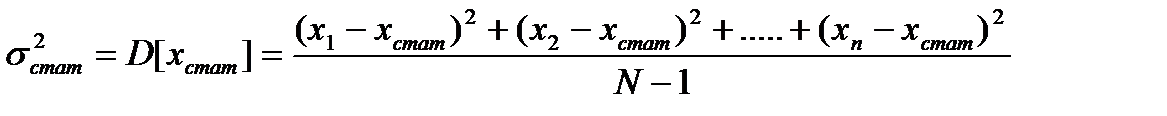 , (2.2)
, (2.2)
где 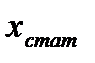 - среднее арифметическое значение величин
- среднее арифметическое значение величин 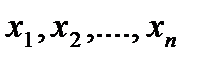 находится по следующей формуле [1]
находится по следующей формуле [1]
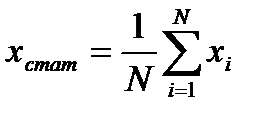 , (2.3)
, (2.3)
где N – общее число измерений, в нашем случае оно равно 72.
Итак по формуле (2.3) вычисляем 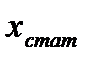
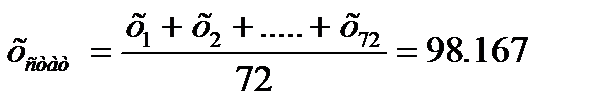
По формуле (2.2) вычисляем 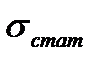
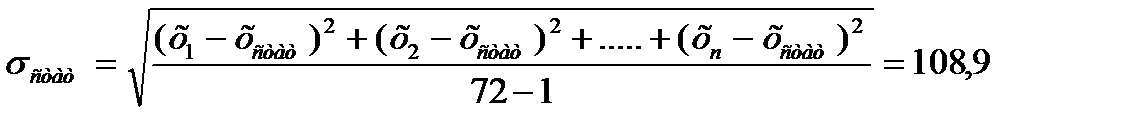
Находим разность двух наибольших и наименьших значений (ПА.таблица1)
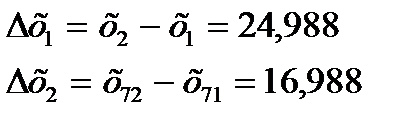
По формуле (2.1) находим 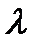 для
для 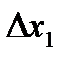 и
и 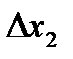
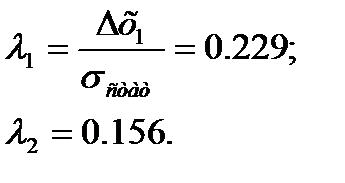
Теперь сверяем, полученные значения 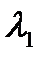 и
и 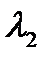 с критическим значением
с критическим значением 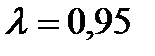 , определяемым по таблице 7.7 [1] в зависимости от объёма выборки N =72.
, определяемым по таблице 7.7 [1] в зависимости от объёма выборки N =72. 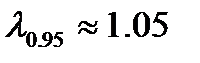 . Видим, что
. Видим, что 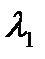 и
и 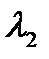 <
< 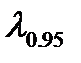 , что говорит о том, что оцениваемые результаты не подлежат исключению из выборки.
, что говорит о том, что оцениваемые результаты не подлежат исключению из выборки.
Метод трёх сигма
Мы хотим исключить ошибки измерения величины 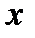 , вероятность появления которых
, вероятность появления которых 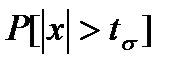 меньше 5% (
меньше 5% (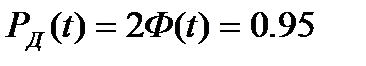 ), т.е. необходимо убрать значения
), т.е. необходимо убрать значения 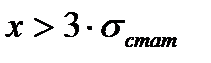 (
(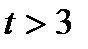 ) [1]. Вычислим отношение:
) [1]. Вычислим отношение:
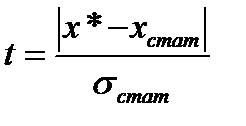
, (2.4)
где 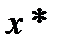 - подозрительное значение из выборки;
- подозрительное значение из выборки; 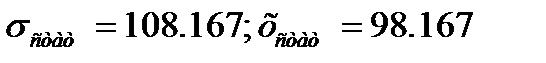
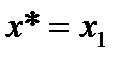 и
и 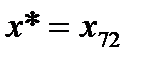 , тогда получим
, тогда получим
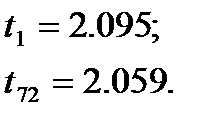
Видим, что 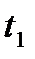 и
и 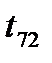 меньше критического значения 3, соответственно измерения
меньше критического значения 3, соответственно измерения 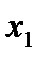 и
и 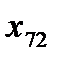 исключать необходимости нет, следовательно, грубых ошибок нет.
исключать необходимости нет, следовательно, грубых ошибок нет.
3 Построение ряда распределения
Расчет проводим по методике [2].
По таблице 1 выбираем наибольшее и наименьшее значение параметра
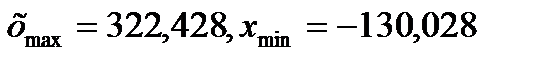
Определяем размах варьирования
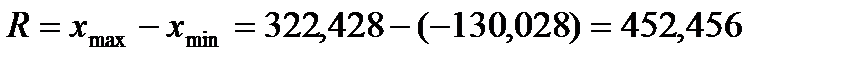 (2.5)
(2.5)
По правилу Стардмесса выбираем число интервалов для количества выборок
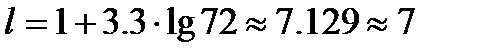 (2.6)
(2.6)
Далее определяем ширину интервала по формуле (2.7)
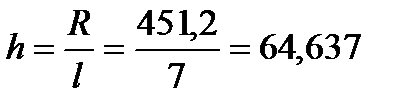 (2.7)
(2.7)
Далее найдем новые границы варьирования по формулам
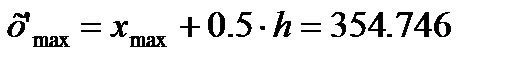 (2.8)
(2.8)
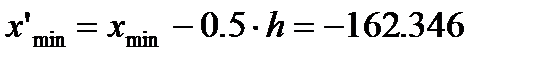 (2.9)
(2.9)
Новы границы варьирования необходимо определять, чтобы не было совпадений крайних границ размаха варьирования с измеренными значениями.
Полученный интервальный ряд распределения приведён в таблице 2.
Таблица 3.1 – Интервальный ряд распределения.
| № | Границы интервалов | Среднее значение интервалов | Частоты, 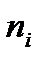
| 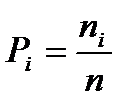
| Накопление част., 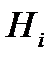
| 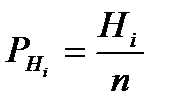
|
| -166,73... -102,273 | -126,18 | 0,028 | 0,028 | |||
| -102,273….-37,816 | -69,693 | 0,111 | 0,139 | |||
| -37,816….26,641 | -9,676 | 0,181 | 0,320 | |||
| 26,641…..91,098 | 58,854 | 0,208 | 0,528 | |||
| 91,098….155,556 | 119,089 | 0,167 | 0,694 | |||
| 155,556….220,012 | 184,43 | 0,181 | 0,875 | |||
| 220,012…..284,469 | 248,75 | 0,097 | 0,972 | |||
| 284,469….348,929 | 303,875 | 0,028 |
4 Построение эмпирических кривых распределения
На основе построенного интервального ряда распределения приведённого в таблице 3.1,построим эмпирические кривые распределения:
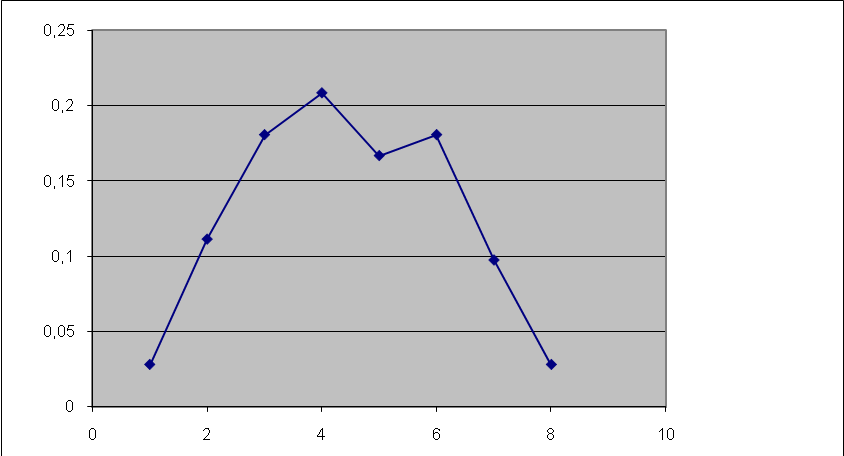
1.) Полигон (рисунок 4.1)
2.)
| Рисунок 4. 2 - Гистограмма |
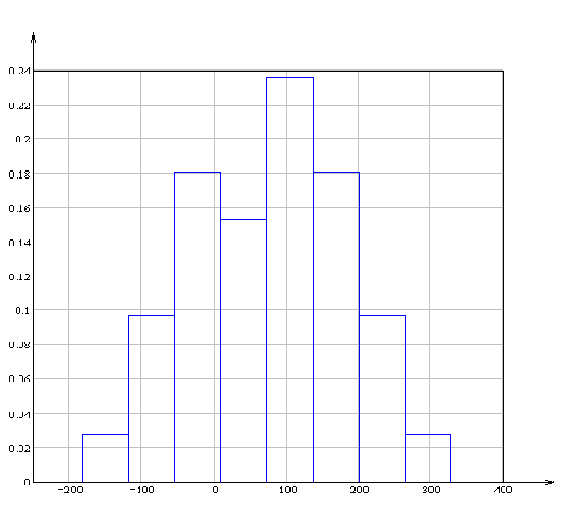 Гистограмма (рисунок 4.2)
Гистограмма (рисунок 4.2)
| Рисунок 4.1 - Полигон |
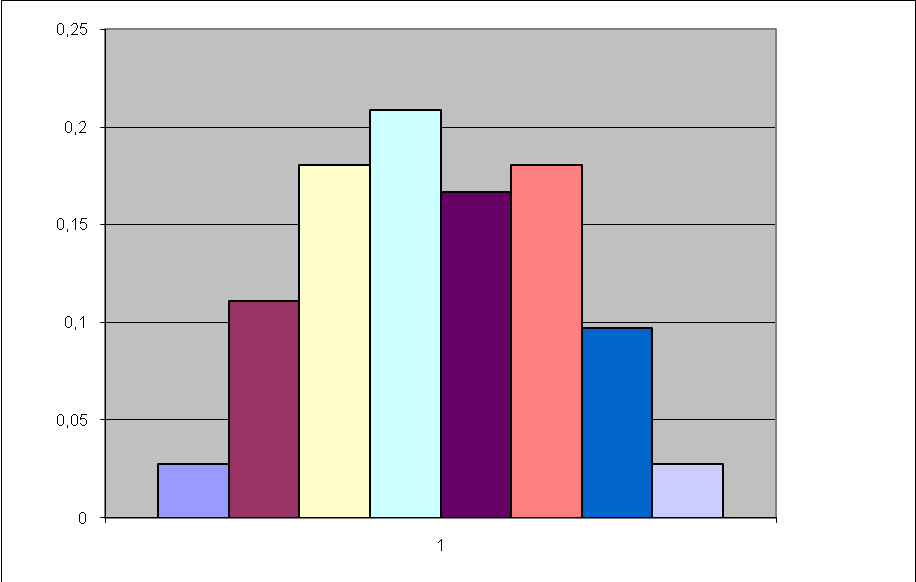
| Рисунок 4.2 - Гистограмма |
Выбор теоретического закона распределения