Разрядность задана, она не может меняться.
Разрядка сетки n-1........0 все это учитывается в алгоритмах работы.
– знаковый разряд.
0 – “+”
1 – “-“
- мантисса числа (число с фиксированной точкой).
- порядок числа (целое число со знаком).
Мантисса всегда хранится в нормализованном виде, т.е. после знакового разряда всегда число отличное от 0.
Число с фиксированной запятой — формат представления вещественного числа в памяти ЭВМ в виде целого числа. При этом само число x и его целочисленное представление 
связаны формулой
, где z — цена (вес) младшего разряда.
Пример арифметики с фиксированной запятой — перевод рублей в копейки. В таком случае, чтобы запомнить сумму 12 рублей 34 копейки, мы записываем в ячейку памяти число 1234.
В случае, если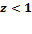 
, для удобства расчётов делают, чтобы целые числа кодировались без погрешности. Другими словами, выбирают целое число u (машинную единицу) и принимают 
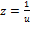. В случае, если 
, его делают целым.
Недостаток фиксированной запятой — очень узкий диапазон чисел, с угрозой переполнения на одном конце диапазона и потерей точности вычислений на другом. Эта проблема и привела к изобретению плавающей запятой.
Название «фиксированная запятая» произошло из-за простой метафоры: между двумя заранее определёнными разрядами ставится запятая, превращая, например, целое число 1234 в дробное 12,34.
Представление чисел со знаком. Прямой и дополнительный коды.
Для представления знаковых целых чисел используются два способа:
1) прямой код;
2) дополнительный код.
Все два способа используют самый левый (старший) разряд битового набора
длины k для кодирования знака числа: знак “плюс” кодируется нулем, а “минус” —
|
|
единицей. Остальные k-1 разрядов (называемые мантиссой или цифровой частью)
используются для представления абсолютной величины числа.
1) Прямой код.
· Целое число.
· Правильная дробь.
ЗЧЧ - значащая часть числа.
Пример.
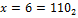
2) Дополнительный код.
· Целое число.
Ноль всегда положительное число.
· Правильная дробь.
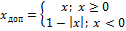
Преобразование числа из прямого кода в дополнительный осуществляется по следующему алгоритму.
1. Если число, записанное в прямом коде, положительное, то к нему дописывается старший (знаковый) разряд, равный 0, и на этом преобразование заканчивается;
2. Если число, записанное в прямом коде, отрицательное, то все разряды числа инвертируются, а к результату прибавляется 1. К получившемуся числу дописывается старший (знаковый) разряд, равный 1.
Пример.
Выявления переполнения разрядной сетки при сложении чисел в дополнительном коде.
При сложении чисел в дополнительном коде возможно переполнение разрядной сетки; для выявления после сложения выполняется анализ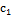 
и 
. Если переносы равны, то переполнения нет, и единица вышедшая за разряд сетки отбрасывается. Если переносы не равны фиксируется переполнение в знаковом разряде бит переполнения значащей части числа, а знак вытеснен за пределы разрядной сетки.
Пример.
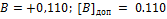
В результате сложения двух положительных чисел получено отрицательное число, что является ошибкой. Результат неверен также и по величине.