Теоретическая часть для лабораторной работы С-5

ЛАБОРАТОРНАЯ РАБОТА С-5

«СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ВЗАИМОСВЯЗИ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ЯВЛЕНИЙ»

Цель работы: приобретение навыка в построении линейного уравнения регрессии для эмпирических данных, в нахождении параметров уравнения на основе этих данных; в расчёте коэффициента тесноты связи изучаемых признаков с использованием инструментария Microsoft Excel; проведении анализа на основе полученных результатов.

 

Самостоятельная подготовка студентов к выполнению лабораторной работы включает:

1. Изучение теоретического материала по теме «Статистическое изучение взаимосвязи социально-экономических явлений».

2. Подбор информации по заданной тематике, используя Интернет-ресурсы, с целью работы с ней в лаборатории. Требования к информации: формирование массива информации из как минимум двух факторных признаков и одного результативного признака. Массив информации по каждому признаку должен представлять собой пространственную выборку (экономические показатели по регионам, по отраслям деятельности на конкретный момент времени), минимальное число показателей для анализа – 30.

 

Задание для работы в лаборатории

1. Выполнить качественный (теоретический) анализ предварительно подготовленной информации, на основе которого устанавливается результативный признак, признаки-факторы и их измерители.

2. Осуществить проверку первичной информации о величине результативного и факторных признаков на однородность и нормальность распределения.

3. Исключить резко выделяющиеся (аномальные) единицы из массива первичной информации, сформировать новый массив для последующего анализа корреляционной зависимости и определить для него основные статистические характеристики.

4. Установить факт наличия парной корреляционной зависимости и ее направления.

5. Определить форму уравнения связи парной корреляционной зависимости.

6. Измерить степень тесноты парной корреляционной зависимости.

7. Найти аналитическое выражение парной зависимости (уравнения парной регрессии).

Теоретическая часть для лабораторной работы С-5

 

Статистические распределения характеризуются наличием более или менее значительной вариации в величине признака у отдельных единиц совокупности. Изучение зависимости вариации признака от окружающих условий составляет содержание теории корреляции.

При изучении конкретных зависимостей одни признаки выступают в качестве факторов, обуславливающих изменение других признаков. Признаки этой первой группы называют признаками-факторами (факторными признаками). Признаки, которые являются результатом влияния этих факторов, называют результативными.

Можно выделить две категории зависимостей между признаками: 1) функциональные; 2) стохастические (частный случай корреляционные).

Функциональные связи характеризуются соответствием между изменением факторного признака и изменением результативной величины, и каждому значению признака-фактора соответствуют определенные значения результативного признака.

Если причинная зависимость проявляется не в каждом отдельном случае, а в общем среднем при большом числе наблюдений, то такая зависимость называется стохастической. Частным случаем стохастической является корреляционная связь, при которой изменение среднего значения результативного признака обусловлено изменением факторных признаков. Парный линейный коэффициент корреляции рассчитывается по формуле:

. (5.1)

Величина коэффициента корреляции колеблется в пределах .

По степени тесноты связи различают количественные критерии оценки тесноты связи (таблица 5.1)

Таблица 5.1 - Количественные критерии оценки тесноты связи

Величина коэффициента корреляции	Характер связи
До	Практически отсутствует
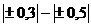
	Слабая
	Умеренная
	Сильная

 

При сравнении функциональных и корреляционных зависимостей следует иметь в виду, что при наличии функциональной зависимости между признаками можно, зная величину факторного признака, точно определить величину результативного признака. При наличии же корреляционной зависимости устанавливается лишь тенденция изменения результативного признака при изменении величины факторного признака.

Последовательность исследования корреляционных зависимостей:

1) предварительный анализ свойств моделируемой совокупности единиц;

2) установление факта наличия связи, определения ее направления и формы;

3) измерение степени тесноты связи между признаками;

4) построение регрессионной модели, т.е. нахождение аналитического выражения связи;

5) оценка адекватности модели, ее экономическая интерпретация и практическое использование.

Для того чтобы результаты корреляционного анализа нашли практическое применение и дали желаемый результат, должны выполняться определенные требования в отношении отбора объекта исследования и признаков-факторов. Важнейшим условием правильного применения методов корреляционного анализа является требование однородности тех единиц, которые подвергаются изучению методами корреляционного анализа. Например, при корреляционном анализе зависимостей показателей деятельности предприятий от определенных факторов, должны быть отобраны предприятия, выпускающие однотипную продукцию, имеющие одинаковый характер технологического процесса и тип используемого оборудования. При выполнении указанных требований далее необходима количественная оценка однородности исследуемой совокупности. Широкое распространение для оценки однородности получил коэффициент вариации.

Другим важным требованием является достаточность числа наблюдений. Влияние существенных причин может быть затушевано действием случайных факторов, «взаимопогашения» влияния которых на результативный показатель происходит при выведении средней результативного показателя для массы случаев.

Требования существуют и в отношении факторов, вводимых в исследование. Все множество факторов, оказывающих влияние на величину результативного показателя, не может быть введено в рассмотрение. В этом нет необходимости, так как их роль и значение в формировании величины результативного показателя могут иметь существенные различия. Поэтому при ограничении числа факторов, включаемых в исследование, наряду с качественным анализом целесообразно использовать и количественные оценки, позволяющие конкретно охарактеризовать влияние факторов на результативный показатель (например, парные коэффициенты корреляции, ранговые коэффициенты корреляции).

Включаемые в исследование факторы должны быть независимыми друг от друга, так как наличие тесной связи между ними свидетельствует о том, что они характеризуют одни и те же стороны изучаемого явления и в значительной мере дублируют друг друга.

Все основные положения теории корреляции разрабатывались в предположении о нормальном характере распределения исследуемых признаков.

Нормальное распределение широко используется в различных сферах человеческой деятельности для приближенного описания случайных явлений, так как требует знания всего двух параметров – среднего значения 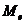и стандартного отклонения 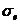. Случайная величина Х имеет нормальное распределение вероятностей с параметрами а и , если плотность ее распределения задается формулой:

(5.2)

Математическое ожидание и дисперсия случайной величины Х соответственно равны и .

Нормальное распределение обладает рядом важнейших свойств, которые приводятся ниже:

Вероятность больших отклонений нормальной случайной величины от центра ее распределения (параметра a ) ничтожно мала.

График функции плотности нормального распределения симметричен относительно средней (параметра а).

Стандартное отклонение характеризует степень сжатия или растяжения графика функции плотности распределения вероятностей.

Нормальная случайная величина с математическим ожиданием а и стандартным отклонением с вероятностью близкой к 1 попадает в интервал . Это утверждение получило название правило трех сигм.

Если случайная величина распределена по нормальному закону распределения с математическим ожиданием а и стандартным отклонением , то

(5.3)

где Ф – функция вероятностей Лапласа.

Эти соотношения позволяют определить вероятность того, что случайная величина Х будет меньше (или больше) заданного значения х.

Таким образом, выявление общего характера распределения предполагает оценку степени его однородности, симметричности, остро- и плосковершинности. Степень однородности распределения определяют с помощью коэффициента вариации:

. (5.4)

Если коэффициент вариации больше 0,33 (или 33%), то распределение можно считать неоднородным.

Симметричным называют распределение, в котором частоты любых двух вариантов, равноотстоящих в обе стороны от центра распределения, равны между собой. Простейшей мерой асимметричности распределения является отклонение между характеристиками центра распределения. Асимметрия тем заметнее, чем больше отклонение .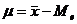

В практических расчетах в качестве асимметрии применяется нормированный коэффициент асимметрии третьего порядка, который не зависит от масштаба, выбранного при измерении варианта, так как является отвлеченной величиной:

. (5.5)

Если , то в ряду распределения преобладают варианты, которые меньше, чем средняя, т.е. ряд отрицательно асимметричен (или с левосторонней скошенностью – более длинная ветвь влево). Если , то для ряда распределения характерна положительная асимметрия (правосторонняя скошенность – более длинная ветвь вправо), при симметричном распределении, так как варианты равноудалены от и имеют одинаковую частоту. Поэтому .

Для определения крутизны (заостренности) распределения вычисляется центральный момент четвертого порядка и определяется нормированный момент четвертого порядка:

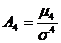. (5.6)

Для нормального распределения 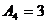. При оценке крутизны в качестве эталонного выбирается нормальное распределение, которое сравнивается с фактическим и вычисляется показатель эксцесса распределения:

(5.7)

При симметричном распределении . Если , то распределение является островершинным, если 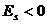- плосковершинным. В результате более при сравнении распределений двух случайных величин при равенстве их средних предпочтительной является величина с большим коэффициентом эксцесса. Для определения значений коэффициентом асимметрии и эксцесса используются функции СКОС () и ЭКСЦЕСС ().

Однако случай, когда и , чисто теоретический. На практике для признания симметричности распределения используют следующее допущение:

если , (5.8)

где (n – число значений случайной величины),

то асимметрия считается несущественной, а ее наличие объясняется воздействием случайных факторов. В противном случае асимметрия статистически значима и факт ее наличия требует дополнительной интерпретации.

Аналогично, если

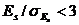, (5.9)

где

то эксцесс считается незначительным и его величиной можно пренебречь.

В целом для проведения предварительного анализа совокупности единиц наблюдений можно воспользоваться инструментом Описательная статистика (СЕРВИС – Анализ данных – Описательная статистика).

В случае невыполнения предпосылок об однородности и нормальности анализируемых случайных величин необходимо провести корректировку исходного массива данных. С этой целью можно воспользоваться «правилом трех сигм». Для каждой случайной величины формируется следующая таблица:

Интервалы значений случайной величины	Количество значений, входящих в интервал	Удельный вес значений, входящих в интервал, в общем их числе, %

Далее из массива первичной информации исключаются все резко выделяющиеся (аномальные) значения, т.е значения, уровень которых не попадает в интервал 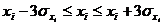. В результате сформирован новый массив данных, который используется в дальнейшем анализе. Однако для этого массива тоже предварительно рассчитываются основные характеристики.

Установление факта наличия и направления корреляционной зависимости между результативным и факторным признаком осуществляется методом аналитических группировок. Чтобы выявить зависимость с помощью этого метода, нужно произвести группировку признака по признаку-фактору и для каждой группы вычислить среднюю или относительную величину результативного признака. Сопоставляя затем изменение результативного признака по мере изменения признака–фактора, можно выявить наличие и направление связи между ними.

На основе данных аналитической группировки следует построить график эмпирической линии связи (линию регрессии), внешний вид которой позволяет судить не только о наличии, но и о форме корреляционной связи. На основе построенного графика эмпирической линии связи формулируется вывод о предположительной форме корреляционной связи.

Для определения тесноты линейной зависимости служит линейный коэффициент корреляции (r), при криволинейной (нелинейной) зависимости – корреляционное отношение (). В Excel парный линейный коэффициент корреляции может быть рассчитан с помощью функции КОРРЕЛ ().

Определение вида уравнения парной корреляционной зависимости (модели парной линейной регрессии) и численных значений параметров уравнения производится методом наименьших квадратов, для чего решается система нормальных уравнений. В Excel линейные уравнения регрессии можно построить с помощью функции ЛИНЕЙН () (внимание: это функция массива) или инструмента Регрессия (СЕРВИС – Анализ данных - Регрессия). Для ручных вычислений целесообразно результаты расчетов сводить в таблицу, так как на примере ниже.

 

Пример построения парного линейного уравнения регрессии

По семи территориям Уральского района за 200Х г. известны значения двух признаков (таблица 5.1).

Таблица 5.1 Исходные данные

Район	Среднедневная заработная плата одного работающего, руб., х	Расходы на покупку продовольственных товаров в общих расходах, %, у
Удмуртская респ.	45,1	68,8
Свердловская обл.	59,0	61,2
Башкортостан	57,2	59,9
Челябинская обл.	61,8	56,7
Пермская обл.	58,8	55,0
Курганская обл.	47,2	54,3
Оренбургская обл.	55,2	49,3

 

Требуется:

1. Для характеристики зависимости у от х рассчитать параметры парного линейного уравнения регрессии.

2. Оценить каждую модель через парный линейный коэффициент корреляции, коэффициент детерминации и среднюю ошибку аппроксимации Ā.

3. Проверить значимость уравнения регрессии по статистике Фишера.

4. Рассчитать коэффициент эластичности.

5. Сделать вывод о пригодности уравнения для практического использования.

Решение

1. Для расчета параметров линейной регрессии 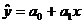решаем систему нормальных уравнений относительно и :

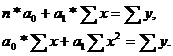
По исходным данным рассчитываем .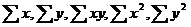

.

.

 

Уравнение регрессии: . С изменением х (например, увеличение) на одну единицу у возрастает на единиц (если ) или уменьшается на единиц (если ). При переходе на конкретные признаки x и у: с увеличением среднедневной заработной платы на 1 руб. доля расходов на покупку продовольственных товаров снижается в среднем на 0,35 %-ных пункта.

Таблица 5.2 – Вспомогательная таблица

	y	x	yx	x2	у2	ŷх	y-ŷх	Ai
	68,8	45,1	3102,88	2034,01	4733,44	61,3	7,5	10,9
	61,2	59,0	3610,80	3481,00	3745,44	56,5	4,7	7,7
	59,9	57,2	3426,28	3271,84	3588,01	57,1	2,8	4,7
	56,7	61,8	3504,06	3819,24	3214,89	55,5	1,2	2,1
	55,0	58,8	3234,00	3457,44	3025,00	56,5	-1,5	2,7
	54,3	47,2	2562,96	2227,84	2948,49	60,5	-6,2	11,4
	49,3	55,2	2721,36	3047,04	2430,49	57,8	-8,5	17,2
Итого	405,2	384,3	22162,34	21338,41	23685,76	405,2	0,0	56,7
Среднее значение	57,89	54,90	3166,05	3048,34	3383,68	X	X	8,1
	5,74	5,86	X	X	X	X	X	X
	32,92	34,34	X	X	X	X	X	X

 

Рассчитаем линейный коэффициент парной корреляции:

.

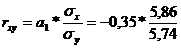Связь умеренная, обратная.

Определим коэффициент детерминации:

 

Вариация результата на 12,7% объясняется вариацией факторах. Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчетные) значения у_х. Найдем величину средней ошибки аппроксимации Ā:

 

=

 

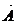В среднем расчетные значения отклоняются от фактических на 8,1%.

Рассчитаем F-критерий:

,

где n – число значений признака,

m – число факторов в уравнении регрессии.

(при уровне значимости =0,05 и числе степеней свободы .

.

Рассчитаем коэффициент эластичности:

.

Это означает, что при увеличении среднедневной заработной платы одного работающего (т.е. х) на 1% расходы на покупку продовольственных товаров (т.е. у) возрастают на 0,33%.

Полученное значение указывает на необходимость принять ги­потезу Н_о о случайной природе выявленной зависимости и статистической незначимости уравнения регрессии и показателя тесноты связи.

5.3 Контрольные вопросы для подготовки лабораторной работы к защите

1. Назовите основные количественные характеристики, используемые для измерения статистической зависимости между случайными величинами?

2. Какие функции и инструменты Excel следует использовать для анализа степени зависимости между случайными величинами?

3. Для чего используется инструмент Анализ данных - Описательная статистика?

4. Дайте краткую характеристику каждому параметру описательной статистики.

5. Какие параметры описательной статистики можно использовать для проверки гипотезы о нормальном распределении случайной величины?

6. Какой показатель является центром распределения случайной величины? Перечислите его основные свойства и приведите формулу для его исчисления.

7. Какие показатели используются для оценки разброса случайной величины? Как определить коэффициент вариации?

8. Дайте определение нормального закона распределения, назовите его свойства.

9. В чем заключается «правило трех сигм»?

10. Для чего используется формула распределения вероятностей Лапласа?

11. Изложите содержание метода наименьших квадратов. Поясните, как используется метод наименьших квадратов для построения уравнения парной линейной регрессии.

12. Какие виды зависимостей вы знаете? Что такое функциональная зависимость? Что такое стохастическая зависимость? Что такое корреляционная зависимость?

13. Как рассчитывается коэффициент парной линейной корреляции? Каким образом его можно рассчитать в Excel?

14. Каким образом с помощью Excel можно построить уравнение регрессии? Уравнение какой регрессии можно построить с помощью функции ЛИНЕЙН? Уравнение какой регрессии можно построить с помощью инструмента Excel Анализ данных – Регрессия.

15. Для каких целей используется коэффициент корреляции в анализе уравнения регрессии?

16. Для каких целей используется коэффициент детерминации в анализе уравнения регрессии?

17. Для каких целей используется коэффициент эластичности?

18. Для каких целей используется ошибка аппроксимации?

19. Какие выводы позволяет сделать оценка регрессии с помощью статистики Фишера? Каким образом находят табличное значение статистики Фишера? Каким образом рассчитывается фактическое значение статистики Фишера?

20. Имеются данные о связи между средней взвешенной ценой и объемом продаж акций:

 

Вид	Средняя взвешенная цена, руб. X	Объем продаж, тыс. руб. У
А
Б
В
Г
Д

На основе парного линейного коэффициента корреляции охарактеризуйте тесноту и направление взаимосвязи между указанными признаками.

 

ЛАБОРАТОРНАЯ РАБОТ С-6

«РЯДЫДИНАМИКИ. ПОСТРОЕНИЕ ХАРАКТЕРИСТИК ДИНАМИЧЕСКИХ РЯДОВ»

 

Цель работы: освоение принципов построения цепных и базисных характеристик рядов динамики, приобретение навыков расчета средних характеристик динамических рядов. Проведение анализа на основе полученных результатов.

Самостоятельная подготовка студентов к выполнению лабораторной работы включает:

1. Изучение теоретического материала по теме «Ряды динамики».

2. Подбор информации по заданной преподавателем тематике, используя Интернет-ресурсы, с целью работы с ней в лаборатории. Требования к информации: - динамические ряды абсолютных или относительных показателей, минимальное число показателей для анализа – 3, минимальное количество уровней динамического ряда конкретного показателя – 20.