В начальный момент 
к последовательному 
контуру подключается гармоническая э.д.с. Дифференциальное уравнение для данной цепи, составленное на основании уравнения Кирхгофа, имеет вид:
, (1.35)
а его решение 
. Здесь 
- ток свободных колебаний, а 
- вынужденный ток.
Аналогичное уравнение записывается для напряжения на емкости 
, (1.36)
решение которого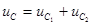 
.Здесь 
- напряжение на емкости, соответствующее свободным колебаниям в контуре. Выражение для этого напряжения можно записать, пользуясь полученным ранее выражением (l.23) при рассмотрении свободных колебаний в контуре. Запишем выражение для напряжения в виде
.
Тогда для тока свободных колебаний получим выражение
.
Для контуров с достаточной добротностью (
) можно считать 
, 
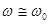и поэтому
При воздействии гармонической э.д.с, установившийся ток в контуре имеет вид
,
где 
и 
. Установившееся напряжение на емкости принимает вид
,
Тогда общее решение уравнения (l.35)
.
Для напряжения на емкости в переходном режиме получаем выражение
.
Для определения констант 
и 
воспользуемся начальными условиями задачи. Если до включения э.д.с, в контуре не была запасена энергия, то при , 
и 
.Отсюда находим:
,
.
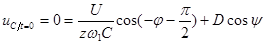Заменяя здесь 
на 
и деля второе уравнение на 
, из получающихся уравнений находим 
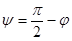и 
:
и 
При этом для тока и напряжения получаем обратные решения:
(1.37)
(1.38)
В случае, когда частота э.д.с. совпадает с частотой контура, т.е. 
имеем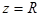 
, 
и выражения для тока и напряжения упрощаются
, (1.39)
. (1.40)
На рис.1.14 приведена осциллограмма напряжения как сумма напряжения свободных колебаний 
и напряжения вынужденных колебаний 
. По мере затухания свободных колебаний растет амплитуда результирующего колебания. Огибающая амплитуды напряжения 
изменяется по экспоненциальному закону
|
|
.
Величина амплитуды установившегося колебания зависит от добротности контура. Процесс установления колебаний заключается в постепенном заряде емкости и накоплении энергии в ней. Так как частота э.д.с. 
и собственная частота контура равны, то при смене знака э.д.с. ток в контуре также меняет направление, что приводит к увеличению заряда на емкости. Напряжение на емкости растет до того момента времени, пока энергия потерь в активном сопротивлении 
, возрастая с ростом тока в контуре, не сравняется с энергией, поступающей в контур за счет источника э.д.с.
Процесс установления колебаний практически считается законченным, когда амплитуда напряжения на емкости (или ток в контуре) достигает 95% своего стационарного значения, т.е. можно записать
,
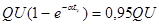или время установления
.
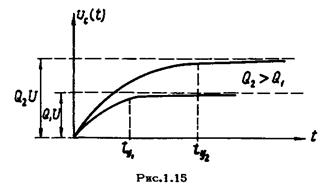
На рис.1.15 показана огибающая амплитуд напряжения на емкости для различных значений добротности контура. С ростом добротности 
увеличивается время установления 
, но и растет амплитуда установившихся колебаний.
Если частота э.д.с, не совпадает с собственной частотой контура 
, то, как показывает анализ выражения (1.37), закон нарастания колебаний более сложен (см.рис.1.16). Здесь огибающая тока в контуре (или напряжения на емкости) изменяется по колебательному закону. Вначале ток 
растет до величины, превышающей его стационарное значение, а затем, осциллируя, уменьшается по амплитуде и при 
его амплитуда приближается к стационарному значению 
, где 
- модуль импеданса контура. Частота осцилляции огибающей амплитуды этого сложного колебания равна разности частот 
.
|
|
