Задача 1. Чертов 25. 47
Задача 2. Найти отношение амплитудных значений плотности тока смещения и проводимости в диэлектрике, у которого удельное сопротивление ρ=1012 Ом*м, ε=10. Колебания электрического поля в диэлектрике происходят по закону Е=Еm cos(ωt), где ω=107 рад/ с.
Задача 3. Две заряженные проводящие плоскости радиусом R имеют поверхностные плотности |σ1|=| σ2|. Их замкнули накоротко. Считая, что в первый момент времени разрядный ток будет постоянным (Iпр=const), найти индукцию магнитного поля В, возникающую в первые моменты.
Задача 4. Площадь пластин конденсатора S=60 см2, первоначальное расстояние между ними d0=10 мм. Пластины конденсатора стали раздвигать со скоростью v=3 мм/ мин. Начальный заряд конденсатора q0=1 нКл. Определить модуль плотности тока смещения через 20 с после начала раздвижения, если:
1. Конденсатор отключен от источника напряжения;
2. Разность потенциалов между обкладками остается постоянной.
Задача 5. Плотность тока смещения в некоторой точке диэлектрика с диэлектрической проницаемостью ε меняется со временем по закону j cм =0.002 cos(104t) А/м2. По какому закону меняется напряженность электрического поля Е(t).
Задача 6. (ИР. 3.366) Длинный прямой соленоид имеет n витков на единицу длины. По нему течет переменный ток I=Im sin(ωt). Найти плотность тока смещения как функцию расстояния r от оси соленоида. Радиус сечения соленоида R,
Задача 7. (ИР.3.365) Пространство между обкладками плоского конденсатора, имеющего форму круглых дисков, заполнено однородной слабо проводящей средой с удельной проводимостью σ и диэлектрической проницаемостью ε. Расстояние между обкладками d. Пренебрегая краевыми эффектами, найти напряженность магнитного поля между обкладками на расстоянии r от их оси, если на конденсатор подано переменное напряжение U=Um cos(ωt).
Дома 25. 48, 49
Тест «ЭМИ. Уравнения Максвелла»
19. Резервное
________________________________________________________________________
Задачи для подготовки к экзамену РтФ - Ч.1
I. Механика
1. Зависимость пройденного телом пути от времени дается уравнением S = B + 2Ct + Dt3, где B =6 м, C=3 м/с, D= - 0,5 м/с3 - постоянные величины. Определить момент времени, когда скорость тела будет равна нулю, а также значение ускорения в этот момент времени.
2. Камень брошен горизонтально со скоростью v0 =18 м/с. Найти нормальное an и тангенциальное at ускорения тела через время t = 1 с после начала движения. Каков радиус кривизны траектории в этой точке?
3. Камень, брошеный горизонтально, через время t = 0,5 с после начала движения имел скорость в 1,5 раза больше скорости v0 в момент бросания. С какой скоростью v0 был брошен камень?
4. Тело брошено со скоростью v0 = 14,7 м/с под углом a = 300 к горизонту. Найти нормальное an и тангенциальное at ускорения тела через время t = 1,25 с после начала движения.
5. Тело массой m = 1 кг движется прямолинейно, причем зависимость пройденного телом пути от времени дается уравнением S = A + Bt + Ct2—Dt3, где C =5 м/с2 и D =1 м/с3. Определите силу, действующую на тело в конце первой секунды движения.
6. Тело скользит по наклонной плоскости, образующей с горизонтом угол 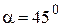 . Зависимость пройденного телом пути от времени дается уравнением
. Зависимость пройденного телом пути от времени дается уравнением  , где
, где  м/с2. Найти коэффициент трения m тела о плоскость.
м/с2. Найти коэффициент трения m тела о плоскость.
7. Самолет поднимается и на высоте h = 5 км достигает скорости v = 360 км/ч. Во сколько раз работа A 1, совершаемая при подъеме против силы тяжести, больше работы A 2, идущей на увеличение скорости самолета?
8. Найти работу, которую надо совершить, чтобы увеличить скорость движения тела от 2 м/с до 8 м/с на пути в 15 м. На всем пути действует сила трения равная 3 Н. Масса тела – 1,5 кг.
9. С башни высотой 25 м горизонтально брошен камень со скоростью 20 м/с. Найти кинетическую и потенциальную энергию камня спустя 1,5 секунды после начала движения. Масса камня 0,1 кг. Сопротивлением воздуха пренебречь.
10. Автомобиль массой 3 т движется по наклонной плоскости вверх с постоянной скоростью. Найти силу тяги автомобиля, если угол наклонной плоскости 30°, а коэффициент трения 0,03.
11. Камень бросили под углом a = 60° к горизонту со скоростью v0 =14 м/с. Масса камня m = 0,2 кг. Сопротивлением воздуха пренебречь. Найти кинетическую и потенциальную энергию камня в высшей точке траектории.
12. Тело массы m =1 кг бросили вертикально вверх с поверхности земли с начальной скоростью ν =10 м/с. Работа силы сопротивления воздуха за все время движения тела составила Ас= -18 Дж. Определить с какой скоростью тело упало на землю.
13. Конькобежец массой 60 кг, стоя на коньках на льду, бросает в горизонтальном направлении камень массой 3 кг со скоростью 8 м/с. На какое расстояние откатится при этом конькобежец? Коэффициент трения коньков о лед 0,001.
14. Тело массой 0,3 кг, двигающееся со скоростью 5 м/с, сталкивается с неподвижным телом массой 0,7 кг. Считая удар абсолютно неупругим, найти: скорость тел после столкновения и работу неконсервативных сил за время удара.
15. Ядро массой 25 кг, двигаясь горизонтально со скоростью 300 м/с попадает в вагон с песком, который может свободно двигаться по рельсам и застревает в нем. Определить количество теплоты, выделившееся в результате этого, если масса вагона с песком 3 т.
16. Из орудия массой 5 т вылетает снаряд массой 100 кг. Кинетическая энергия снаряда при вылете 7,5 Мдж. Какую кинетическую энергию получает орудие вследствие отдачи.
17. Камень, пущенный по поверхности льда со скоростью 2 м/с, прошел до полной остановки расстояние 20,4 м. Найти коэффициент трения камня по льду, считая его постоянным.
18. Колесо вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением  , где B = 1,0 рад/c, C = 1,0 рад/c2, D = 1,0 рад/c3. Найти радиус R колеса, если известно, что к концу второй секунды движения, для точек, лежащих на ободе колеса, нормальное ускорение an = 3,46 м/c2.
, где B = 1,0 рад/c, C = 1,0 рад/c2, D = 1,0 рад/c3. Найти радиус R колеса, если известно, что к концу второй секунды движения, для точек, лежащих на ободе колеса, нормальное ускорение an = 3,46 м/c2.
19. Однородный диск радиусом 0,2 м и массой 5 кг вращается вокруг оси, проходящей через его центр перпендикулярно к его плоскости. Зависимость угловой скорости вращения диска от времени дается уравнением  , где С = 8 рад/с2. Найти касательную силу, приложенную к ободу диска. Трением пренебречь.
, где С = 8 рад/с2. Найти касательную силу, приложенную к ободу диска. Трением пренебречь.
20. Диск радиусом 20 см вращается согласно уравнению  , где А = 3,0 рад/c, B = 1,0 рад/c, C = 0,1 рад/c3 . Определить тангенциальное a τ, нормальное an и полное a ускорения точек на окружности диска для момента времени t = 10 с.
, где А = 3,0 рад/c, B = 1,0 рад/c, C = 0,1 рад/c3 . Определить тангенциальное a τ, нормальное an и полное a ускорения точек на окружности диска для момента времени t = 10 с.
21. Колесо, вращаясь равнозамедленно, за время t = 60 с уменьшило свою частоту с n 1 = 300 об/мин до n 2 = 180 об/мин. Найдите угловое ускорение e колеса и число оборотов N колеса за это время.
22. Колесо автомашины вращается равноускоренно. Сделав N = 50 полных оборотов, оно изменило частоту вращения от n1 = 4 c-1 до n2 = 6 c-1. Определите угловое ускорение колеса.
23. К ободу однородного диска радиусом R = 0,2 м приложена касательная сила F = 98,1 Н. При вращении на диск действует момент сил трения M тр = 4,9 Н×м. Найти массу диска, если диск вращается с угловым ускорением e = 100 рад/с2.
24. На барабан радиусом 0,5 м намотан шнур, к концу которого привязан груз массой 10 кг. Найти момент инерции I барабана, если известно, что груз опускается с ускорением 2,04 м/c2.
25. Через блок, имеющий форму диска, перекинут шнур. К концам шнура привязаны грузики массой m1 = 100 г и m2 = 110 г. С каким ускорением будут двигаться грузики, если масса блока m = 400 г? Трение при вращении блока ничтожно мало.
26. К ободу диска массой m = 5 кг приложена касательная сила F = 20 Н. Какую кинетическую энергию будет иметь диск через t = 5 с после начала действия силы?
27. Маховик в виде диска массой 80 кг и радиусом 30 см находится в состоянии покоя. Определить работу внешних сил при сообщении маховику частоты вращения 12 об/с.
28. Колесо, вращаясь равнозамедленно, уменьшило за 1 мин частоту вращения от 300 об/мин до 180 об/мин. Момент инерции колеса 2 кг×м2. Найти угловое ускорение колеса; момент сил торможения; работу сил торможения.
29. Маховик в виде диска массой 80 кг и радиусом 30 см находится в состоянии покоя. Определить работу внешних сил при сообщении маховику частоты вращения 10 об/с; работу внешних сил в случае, когда диск при той же массе имел бы радиус в два раза больше.
30. Диск массой 3 кг катится без скольжения по горизонтальной плоскости со скоростью v = 4 м/c. Найти кинетическую энергию диска.
31. Мальчик катит обруч по горизонтальной дороге со скоростью 7,2 км/ч. На какое расстояние может вкатиться обруч на горку за счет своей кинетической энергии. Уклон горки равен 15 м на каждые 100 м пути. Трением пренебречь/
32. Кинетическая энергия вала, вращающегося с частотой n = 5 об/c равна 60 Дж. Найдите момент импульса L вала.
33. Горизонтальная платформа массой m = 100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой n1 = 10 об/мин. Человек массой M = 60 кг стоит при этом на краю платформы. С какой частотой n2 начнет вращаться платформа, если человек перейдет от края к центру платформы? Платформу считать однородным диском, а человека – точечной массой.
II. МКТ. Термодинамика
1. 12 г газа занимают объем V = 4×10–3 м3 при температуре t = 7 °C. После нагревания газа при постоянном давлении его плотность стала равна r = 6×10 –4 г/см3. До какой температуры нагрели газ?
2. Найти среднеквадратическую скорость молекул газа, плотность которого при давлении р = 10 5 Па равна r = 8,2×10 –2 кг/м3. Чему равна молярная масса этого газа, если значение плотности дано для температуры t = 17 °С?
3. В закрытом сосуде находится масса m = 28 г азота при давлении p1 = 100 кПа и температуре t = 270С. После нагревания давление в сосуде повысилось в 6 раз. До какой температуры был нагрет газ? Найдите объем сосуда и количество теплоты, сообщенное газу.
4. В сосуде объемом V = 4 л находятся 4 г углекислого газа (СО2) и 8 г закиси азота (N2O) при температуре 1270 С. Найти давление смеси газов в сосуде.
5. В баллоне вместимостью V = 25 л находится водород при температуре T = 290 К. После того как часть водорода израсходовали, давление в баллоне понизилось на Δр = 0,4 МПа. Определить массу израсходованного водорода.
6. В колбе вместимостью V = 100 см3 содержится некоторый газ при температуре T = 300 К. На сколько понизится давление р в колбе, если вследствие утечки из колбы выйдет N = 1020 молекул.
7. На какой высоте h давление воздуха составляет 80% от давления на уровне моря? Температуру воздуха считать постоянной и равной t =00С.
8. На какой высоте плотность водорода на 30% меньше его плотности на уровне моря? Температуру водорода считать постоянной и равной t =00С.
9. Трехатомный газ массой m = 1 кг и плотностью r = 2 кг/м3 находится под давлением p = 80 кПа. Найдите энергию теплового движения U молекул этого газа.
10. При изобарическом расширении двухатомного газа была совершена работа А = 164 Дж. Какое количество теплоты было сообщено газу при этом расширении?
11. Какую массу углекислого газа можно нагреть при p = const от температуры 200 С до температуры 1000 С количеством теплоты Q = 222 Дж? На сколько при этом изменится средняя кинетическая энергия одной молекулы?
12. При изотермическом расширении 14 г азота, находящегося при температуре 170С была совершена работа А = 960 Дж. Во сколько раз изменилось давление азота при расширении?
13. Работа изотермического расширения массы m = 10 г некоторого газа от объема V1 до объема V2 = 2 V1 оказалась равной A = 575 Дж. Найти среднюю квадратическую скорость молекул газа при этой температуре.
14. Баллон вместимостью 20 л содержит водород при температуре T1 = 300 К и давлении p1 = 0,4 МПа. Каковы будут температура T 2 и давление p 2, если газу сообщить количество теплоты Q = 6 кДж?
15. При изотермическом расширении 1 моль кислорода, имевшего температуру T = 300 К, газу было передано количество теплоты Q = 2 кДж. Во сколько раз увеличился объем кислорода?
16. Один моль одноатомного идеального газа, находящегося при давлении p 1 = 1,0×104 Па, адиабатически расширяется из состояния 1 в состояние 2, совершая работу А = 10 кДж. При этом его температура понизилась в 2 раза. Найти объемы V 1 и V 2 начального и конечного состояния, соответственно.
17. Объем V 1=7,5 л кислорода адиабатически сжимается до объема V 2=1 л, причем в конце сжатия установилось давление р 2=1,6 МПа. Под каким давлением р 1 находился газ до сжатия?
18. Количество n = 1кмоль азота, находящегося при нормальных условиях (температуре t 1 = 00С и давлении p1 = 0,1 МПа), расширяется адиабатически от объема V 1 до V 2 = 5 V 1. Найти приращение внутренней энергии газа и работу, совершенную газом при расширении.
19. Тепловая машина, работающая по циклу Карно, совершает за один цикл работу А=73,5 кДж. Температура нагревателя t 1=1000C, температура холодильника t 2=00 С. Найти КПД h цикла, количество теплоты, получаемое машиной за один цикл от нагревателя, и количество теплоты, отдаваемое за один цикл холодильнику.
20. Тепловая машина, работающая по циклу Карно, за цикл получает от нагревателя количество теплоты Q1 = 2512 Дж. Температура нагревателя Т1 = 400 К, температура холодильника Т2 = 300 К. Найти работу А, совершаемую машиной за один цикло, и количество теплоты Q2, отдаваемое холодильнику за цикл.
21. Азот массой m = 7 г изобарически расширился от объема V1 = 2 л до объема V2 = 6 л. Найти количество теплоты сообщенное азоту и изменение энтропии DS при этом процессе.
22. Во сколько раз следует изотермически увеличить объем 4 молей идеального газа, чтобы его энтропия испытала приращение D S = 23 Дж/ К?
23. Найти приращение D S энтропии при переходе массы m =8 г углекислого газа от объема V 1=10 л при температуре t1=800С к объему V 2=40 л при температуре t 2=3000С.
24. 16 г кислорода нагревается от температуры t1 = 500 С до t2 = 1500 С. Найти приращение энтропии, если нагревание происходит:1) изохорически; 2) изобарически.
25. Найти приращение энтропии при изотермическом расширении 6г гелия от давления p1 = 100 кПа до давления p2 = 50 кПа.
26. Кислород массой 2 кг увеличил свой объем в 5 раз. Найти изменение энтропии, если расширение проходило а) изотермически; б) адиабатно.
27. В результате нагревания m =22 г азота его абсолютная температура увеличилась в n=1,2 раза, а энтропия увеличилась на D S =4,19 Дж/К. При каких условиях производилось нагревание (при постоянном объеме или при постоянном давлении)?
28. Гелий массой m =1,7 кг адиабатически расширили в 3 раза и затем изобарически сжали до первоначального объема. Найти приращение энтропии DS при этом процессе.
29. Найти приращение DS энтропии при превращении массы m =100 г льда (t = -100C) в воду с температурой t =400С. Удельная теплоемкость льда 2100 Дж/ кг*К, удельная теплоемкость воды 4200 Дж/ кг*К, удельная теплота плавления льда = 335кДж/К.
30. Найти приращение DS энтропии при превращении массы m =1 г воды (t = 00C) в пар (tп = 1000С). Удельная теплоемкость воды св=4200 Дж/ кг*К, удельная теплота парообразования r = 2,26 МДж/К.
III. Электростатика
1. Два разноименных и равных по величине заряда q =2 нКл расположены в вершинах при острых углах равнобедренного прямоугольного треугольника на расстоянии  см друг от друга. Определить с какой силой эти заряды действуют на третий заряд q 0= 1 нКл, расположенный в третьей вершине треугольника.
см друг от друга. Определить с какой силой эти заряды действуют на третий заряд q 0= 1 нКл, расположенный в третьей вершине треугольника.
 2. Найти напряженность электрического поля в точке, лежащей посередине между точечными зарядами q 1= -8 нКл и q 2= 4 нКл. Расстояние между зарядами r = 10 см.
2. Найти напряженность электрического поля в точке, лежащей посередине между точечными зарядами q 1= -8 нКл и q 2= 4 нКл. Расстояние между зарядами r = 10 см.
3. На рисунке AA- заряженная бесконечная плоскость с поверхностной плотностью заряда s = 40 мкКл/м2 и В – одноименно заряженный шарик массой 1г и зарядом q = 1 нКл. Какой угол a с плоскостью АА образует нить, на которой висит шарик?
4. Две бесконечно длинные равномерно заряженные нити с линейной плотностью заряда t=5,0*10-5 Кл/м расположены на расстоянии а =0,1 м друг от друга. Найти напряженность электрического поля в точке, находящейся на расстоянии b =0,1 м от каждой нити.
5. Две параллельные металлические пластины, расположенные в диэлектрике (ε =2,2), обладают поверхностной плотностью заряда σ1 = 3 мк Кл/м2 и σ2 = 2 мкКл/м2. Найти напряженность электрического поля внутри и вне пластин.
6. Найти величину и направление напряженности электрического поля, созданного точечным зарядом q = 18*10-8 Кл и бесконечно длинной заряженной нитью с линейной плотностью заряда t=0,5*10-5 Кл/м, в точке, удаленной от заряда на a= 4,0 см, от нити на расстояние b =3,0 см. Расстояние между зарядом и нитью с = 5,0 см.
7. С какой силой F l (на единицу длины) отталкиваются две одноименно заряженные бесконечно длинные нити с одинаковой линейной плотностью заряда t= 5 мкКл/м, находящиеся на расстоянии r 1 =30 мм друг от друга? Какую работу Аl (на единицу длины) надо совершить, чтобы сблизить нити до расстояния r 2 =10 мм?
8. Два шарика одинакового радиуса и массы подвешены на нитях одинаковой длины так, что их поверхности соприкасаются, Какой заряд надо сообщить шарикам, чтобы сила натяжения стала равной Т = 98 мН? Расстояние от точки подвеса до центра шарика l = 10 см; а масса каждого шарика m = 4 г.
9. С какой силой Fl электрическое поле заряженной бесконечной плоскости действует на единицу длины заряженной бесконечно длинной нити, помещенной в это поле? Линейная плотность заряда на нити l = 5 мкКл/м и поверхностная плотность заряда на плоскости s = 30 мкКл/м2.
10. Найти силу, действующую на заряд q = 2 нКл, если заряд помещен на расстоянии r = 4 см от заряженной нити с линейной плотностью заряда l = 0,3 мкКл/м.
11. Расстояние между двумя точечными зарядами q 1= -0,33 мкКл и q 2= 0,33 мкКл равно а =10 см. Найти напряженность поля в точке, находящейся на перпендикуляре, восстановленном к середине линии, соединяющей лба заряда на расстоянии b =10 см от нее.
12. Найти силу, действующую на заряд q = 3 нКл, если заряд помещен на расстоянии r = 2 см от заряженной нити с линейной плотностью заряда l = 0,1 мкКл/м.
13. Около заряженной бесконечно протяженной плоскости находится точечный заряд
q = 7,0*10-7 Кл. Под действием поля заряд перемещается по силовой линии на расстояние D r = 2 см, при этом силы поля совершают работу А = 5,0*10-6 Дж. Найти поверхностную плотность заряда на плоскости.
14. Какая работа А совершается при перенесении точечного заряда q = 10 нКл из бесконечности в точку, находящуюся на расстоянии r = 0,5 см от поверхности шара радиусом R = 1 см с поверхностной плотностью заряда s = 10 мкКл/м2.
15. Два шарика с зарядами q 1 =7,0 нКл и q 2 =1,4 нКл находятся на расстоянии r 1 =40 см. Какую работу надо совершить, чтобы сблизить их до расстояния r 2 =25 см?
16. Найти потенциал j точки поля, находящейся на расстоянии r = 12 см от поверхности заряженного шара радиусом R = 2 см, если потенциал шара j0 = 300 В.
17. Шарик, заряженный до потенциала j = 792 В, имеет поверхностную плотность заряда s = 333 нКл/м2. Найдите радиус шарика.
18. Шарик с массой m = 1,5 г и зарядом q = 15 нКл перемещается из точки 1, потенциал которой j1 = 600 В, в точку 2, потенциал которой j2 = 0. Найти его скорость в точке 1, если в точке 2 она стала равной V 2 = 30 см/с.
19. Электрон с энергией W k= 6,4×10-17 Дж (в бесконечности) движется вдоль линии напряженности по направлению к поверхности металлической заряженной сферы радиусом R =10 см. Определить минимальное расстояние rmin, на которое приблизится электрон к поверхности сферы, если ее заряд Q = -10 нКл.
20. На расстоянии r 1 = 20 см от бесконечно длинной заряженной нити находится точечный заряд q= 7*10-10 Кл. Под действием поля заряд перемещается до расстояния r 2 = 40 см. При этом силами поля совершается работа А = 5,0*10-6 Дж. Найти линейную плотность заряда нити t.
21. Электрическое поле образовано положительно заряженной бесконечно длинной нитью. Двигаясь под действием этого поля от точки, находящейся на расстоянии r 1 = 1 см от нити, до точки r 2 = 4 см, a - частица изменила свою скорость от V 1 = 2×105 м/с до V 2 = 3×106 м/с. Найти линейную плотность заряда t на нити. (q a = 3,2×10-19 Кл, m a = 6,69×10-27 кг).
22. Пластины плоского конденсатора площадью S =0,01 м2 каждая притягиваются друг к другу с силой F = 40 мН. Пространство между пластинами заполнено стеклом (e=6). Найти заряды q пластин, напряженность Е поля между пластинами и объемную плотность энергии w поля.
23. Электрическое поле образовано двумя параллельными пластинами, находящимися на расстоянии d =2 см друг от друга. К пластинам приложена разность потенциалов U =140 В. Какую скорость получит электрон под действием поля, пройдя по линии напряженности расстояние s =5 мм?
24. Электрон, пройдя в плоском конденсаторе путь от одной пластины до другой, приобретает скорость v = 106 м/с. Расстояние между пластинами d = 5,3 мм. Найти разность потенциалов U между пластинами, напряженность Е электрического поля конденсатора и поверхностную плотность заряда s на его пластинах.
25. Электрон влетает в плоский горизонтально расположенный конденсатор параллельно его пластинам со скоростью u0 = 107 м/c. Напряженность поля в конденсаторе E = 10 кВ/м, длина конденсатора l = 4 см. Найти модуль и направление скорости электрона при вылете его из конденсатора.
26. Протон влетает в плоский горизонтально расположенный конденсатор параллельно его пластинам со скоростью u0 =1,4 105 м/c. Напряженность поля в конденсаторе E = 3,7 кВ/м, длина конденсатора l = 16 см. Во сколько раз скорость протона при вылете из конденсатора будет дольше его начальной скорости?
27. Между пластинами плоского конденсатора, находящимися на расстоянии d = 5 мм друг от друга приложена разность потенциалов U = 150 В. К одной из пластин прилегает плоскопараллельная пластинка фарфора толщиной d 1 = 3 мм. Найти напряженности E 1 и E 2 в фарфоре и воздухе. Диэлектрическая проницаемость фарфора e = 6.
28. Плоский конденсатор заполнен диэлектриком и на его пластины подана некоторая разность потенциалов. Его энергия при этом W = 20 мкДж. После того как конденсатор отключили от источника напряжения, диэлектрик вынули. Работа, которую надо было совершить против сил электрического поля, чтобы вынуть диэлектрик, А =70 мкДж. Найти диэлектрическую проницаемость e диэлектрика.
29. Площадь пластин плоского воздушного конденсатора S = 0,01 м2, расстояние между ними d 1 = 1 мм. К пластинам приложена разность потенциалов U =100 В. Пластины раздвигаются до расстояния d 2=25 мм. Найти энергии W 1 и W 2 до и после раздвижения пластин если источник напряжения перед раздвижением: а) не отключается, б) отключается
30. Площадь пластин плоского воздушного конденсатора S =0,02 м2, расстояние между ними d = 5мм. Какая разность потенциалов была приложена к пластинам конденсатора, если известно, что при разряде конденсатора выделилось Q =6,2 мДж тепла?
31. Плоский воздушный конденсатор состоит из двух круглых пластин радиусом r = 10 см каждая. Расстояние между пластинами d 1 = 1 см. Конденсатор зарядили до разности потенциалов U = 1 кВ и отключили от источника питания. Какую работу нужно совершить, чтобы, удаляя пластины друг от друга, увеличить расстояние между ними до d 2 = 3,5 см?
IV. Постоянный ток.
1. Найдите падение напряжения U на медном проводе длиной l = 300 м и диаметром d = 1,5 мм, если ток в нем I = 2А. Удельное сопротивление меди r = 17 нОм×м.
2. Какова длина l медного проводника, если при разности потенциалов U = 0,34В на его концах, плотность тока в нем j = 10 А/мм2. Удельное сопротивление меди r = 17 нОм×м.
3. Вольфрамовая нить электрической лампочки при t 1 = 200 С имеет сопротивление R 1 = 35,8 Ом. Какова будет температура лампочки, если при включении в сеть с напряжением U = 120 В по нити идет ток I = 0,33A? Температурный коэффициент сопротивления вольфрама a = 4,6×10-3 К-1.
4. По проводнику диаметром d = 1 мм течет ток силой I = 3,14 А. Концентрация свободных электронов в проводнике n = 2,5×1028 м-3, заряд электрона q = 1,6×10-19 Кл. Какова средняя скорость направленного движения электронов в проводнике?
5. Сколько электронов пройдет за время t = 32 с через поперечное сечение провода диаметром d = 2 мм, длиной l = 10 м при разности потенциалов на его концах U = 3,2 В? Удельное сопротивление алюминия r = 28 нОм×м, заряд электрона e = 1,6×10-19 Кл.
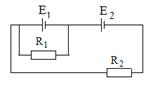
6. Два одинаковых элемента e1 = e2 = 2 В, r1 = r2 = 0,5 Ом. Найти токи I1 и I2, текущие через сопротивления R1 = 0,5 Ом, R2 = 1,5 Ом, а также ток I через элемент с e1.

7. Элементы питания имеют ЭДС e1 = 2 В, e2 = 4 В и e3 = 6 В, сопротивления R1 = 4 Ом, R2 = 6 Ом, R3 = 8 Ом. Найти токи во всех участках цепи.

8. ЭДС элементов e1 = 2,1 В и e2 = 1,9 В, сопротивления R1= 45 Ом, R2= 10 Ом, R3= 10 Ом. Найти токи во всех участках цепи.
 9. Напряжение на зажимах элемента в замкнутой цепи U=2,1 В, сопротивления R1= 5 Ом, R2= 6 Ом, R3= 3 Ом. Какой ток показывает амперметр?
9. Напряжение на зажимах элемента в замкнутой цепи U=2,1 В, сопротивления R1= 5 Ом, R2= 6 Ом, R3= 3 Ом. Какой ток показывает амперметр?
 10.
10.
Две батареи аккумуляторов (e1=10 В, r1=1 Ом, e2=8 В, r2=2 Ом) и реостат (R = 6 Ом) соединены так как показано на рисунке. Найти силу тока в батареях и реостате.
 11. ЭДС батареи e=100 В, сопротивления R1= 100 Ом, R2= 200 Ом,
11. ЭДС батареи e=100 В, сопротивления R1= 100 Ом, R2= 200 Ом,
R3= 300 Ом, сопротивление вольтметра Rv= 2 кОм. Какую разность потенциалов показывает вольтметр?