Функция распределения. Распределение молекул по модулю скорости теплового движения в равновесном состоянии (функция Максвелла). Наиболее вероятная, среднеарифметическая и среднеквадратическая скорости молекул. Распределение молекул в поле силы тяжести (барометрическая формула). Распределение Больцмана. Степени свободы газовых молекул и принцип равнораспределения энергии теплового движения по степеням свободы. Энергия теплового движения в газе одно-, двух- и многоатомных молекул.
Задача 1. Определить температуру газообразного азота, при которой скоростям молекул 300 м/с и 600 м/с, соответствуют одинаковые функции распределения.
Задача 2. Найти скорость газообразного азота, при которой значение f(v) для температуры Т0 будет такой же, как и для температуры в n раз большей.
Задачи:В классе 9. 28, 10.17, 10.16, 19, 26, 4, 9
Дома 10.18, 20, 28, 40, 5-7
Упр.8 Первое начало термодинамики
Количество теплоты и работа как величины, характеризующие процесс обмена энергией между системой и окружением. Внутренняя энергия. Первое начало термодинамики. Теплоемкость газов. Процессы в газах – изохорический, изобарический, изотермический и адиабатический (уравнение, работа, запись первого начала, характерные графики, теплоемкость).
Задачи: В классе 11. 4, 16, 32, 35, 48, 57
Дома 11. 6(см пример 1), 17, 33, 36, 50, 56, 58
Упр. 9 Второе начало термодинамики. Энтропия. Тепловые машины
Равновесные и неравновесные самопроизвольные процессы. Микро и макро распределение. Термодинамическая вероятность. Энтропия и её свойства. Энтропия и информация. Связь изменения энтропии с количеством подведенной теплоты. Изменение энтропии в изопроцессах. Второе начало термодинамики. КПД идеальной тепловой машины.
|
|
Задачи: 11.70 - 75, 61, 63, 64,67, 68 65. ИДЗ Термодинамика
Электромагнетизм
Упр. 10. Закон Кулона. Теорема Гаусса. Расчет полей. Закон Кулона. Электростатическое поле. Напряженность. Поток вектора напряженности. Теорема Гаусса. Применение теоремы Гаусса для расчета поля равномерно заряженной плоскости, непроводящего шара, равномерно заряженных нити, цилиндра, пластины.
В классе 13.2, 10, 20; 14., 11, 14, 23, 28
Дома 13. 3, 4, 8, 13, 18; 14. 3, 4, 10, 12, 16, 15, 25, 29,
Тонкое проводящее кольцо радиуса R заряжено с линейной плотностью l = l0cosj,
где l0 = const, j - азимутальный угол. Найти модуль напряженности электрического поля в центре кольца.
Упр. 11. Потенциал. Связь Е и потенциала. Работа по перемещению заряда
Потенциал. Связь напряженности и потенциала. Потенциальный характер электростатического поля, теорема о циркуляции вектора напряженности.
В классе 15. 8, 15, 22, 29, 31, 47, 56, 66 Дома 15. 6, 14, 16, 24, 28, 45, 49, 58, 61
Упр. 12. Электроемкость. Конденсаторы. Энергия электрического поля
Проводники в электрическом поле. Напряженность поля вблизи поверхности заряженного проводника. Электроемкость. Конденсаторы. Электроемкость плоского, цилиндрического и сферического конденсаторов. Энергия заряженного конденсатора. Плотность энергии электростатического поля.
В классе: 17. 4, 5, 12, 16 18. 4, 5., 16, 18
14.36 или 38, 43
Напомнить: раздвигают пластины конденсатора, как меняются q, U, C, если конденсатор отключен или подключен к источнику; две заряженные сферы соединяют проволочкой, найти заряды и потенциал после соединения (см. абитурский задачник). Найти А по перемещению Q в поле нити из т.1. в т.2
|
|
Упр.13 Постоянный ток. Законы Кирхгофа
В классе 19.3, 13, 15, 19, 30, 34, 36
Дома 19.14, 16, 20, 28, 29, 35
Упр. 14. Контрольная «Электростатика+постоянный ток» + «Применение теоремы Гаусса к расчету полей…» и законы Кирхгофа или прием « ИДЗ Электростатика»
Упр.15 Расчет МП, Закон Био – Саварра – Лапласа. Теорема о циркуляции В
Задачи: В классе 21. 18, 22, 26, 27, 31 (а, б, в), обсудить индукцию «толстого» проводника с током (см. пример на лекции)
Дома 21. 6, 8, 10, 14, 19, 20, 21, 24, 31 (г, д, е)
Выдать на дом ИДЗ «Расчет магнитных полей». Сроквыполнения – 1 неделя
Упр16. Электромагнитная индукция. Опыты Фарадея. Закон Фарадея для эдс индукции, правило Ленца. Само- и взаимоиндукция. Экстратоки размыкания и замыкания. Энергия магнитного поля
В классе 24. 9; 25. 13, 18, 11, 22(можно устно), 17, 23,
25. 28, 42, 33, 38, 32, 26. 3 25.7, 16, 18, 22, 24
Дома: 24.10, 22. 3, 25; 25. 29, 30, 31,36, 37,38, 40, 46, 43- 45,26.4
Задача 1. П- образный проводник находится в перпендикулярном магнитном поле, меняющемся по закону В=0.1t. Вдоль параллельных сторон этого проводника перемещают проводник-перемычку с ускорением а =0.1 м/ с2. Длина перемычки b=0.2 м. Найти ЭДС индукции в контуре через 0.2 с после начала движения, если в начальный момент площадь контура и индукция магнитного поля были равны нулю. Индуктивностью контура пренебречь.
Задача2: Получить формулу для взаимной индуктивности тороида и прямого провода, проходящего перпендикулярно плоскости тороида через его центр. Сечение тора – квадрат со стороной а, R – внутренний радиус тороида, N – число витков в его обмотке.
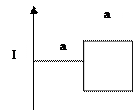
Задача 3. Определить взаимную индуктивность прямого
провода и квадратной рамки со стороной а. Расстояние
между рамкой и проводом равно а.
Упр. 16.А (если будет время): (Сила Ампера и Лоренца):
В классе 22. 6, 27; 23. 11, 22, 30, 36, 39:
Дома 22.9, 17, 16, 23, или 24,