В некой деревни (некотором взводе и т.д.), в которой живет один-единственный парикмахер, был издан указ: "Парикмахер имеет право брить тех и только тех жителей деревни, которые не бреются сами". Может ли парикмахер брить самого себя?
Парадокс "мэр города"
Каждый мэр города живет или в своем городе, или вне его. Был выделен один специальный город, где бы жили мэры, не живущие в своих городах. Где должен жить мэр этого специального города?
Парадокс Кантора (1899)
Согласно одной из теорем немецкого математика Георга Кантора (1845 - 1918), развившего уже упомянутую теорию множеств, не существует самого мощного множества. Сие ввиду того, что для любого сколь угодно мощного множества можно указать еще более мощное. С другой стороны, интуитивно очевидно, что множество всех множеств должно быть самым мощным, ведь оно включает в себя все возможные множества.
Другими словами, пусть множество всех множеств M содержит в себе множество всех своих подмножеств (ведь оно же множество всех множеств). Если первое имеет мощность m, то мощность второго 2m, что больше m. Следовательно, множество M не содержит множество всех своих подмножеств, а, значит, не может быть множеством всех множеств.
Парадокс изобретателя
Начнем с одной из его математических интерпретаций:
Попробуем доказать методом математической индукции неравенство
База при n = 1 очевидна.
Предполагая, что для некоторого k наше неравенство верно, и начиная доказательство для k + 1, получим
и
Нам остается доказать, что
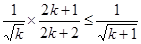- тогда наше неравенство 100% истинно.
Возведем обе части неравенства в квадрат и, после алгебраических преобразований, получим
(k + 1) (2k + 1)2 <= k (2k + 2)2 и, раскрыв скобки,
4k3 + 8k2 + 5k + 1 <= 4k3 + 8k2 + 4k
Здесь мы с ужасом обнаруживаем, что то, что мы получили неверно, а следовательно, и два предыдущих неравенства тоже. Правда, из этого нельзя делать вывод, что неверно и исходное неравенство, а можно лишь тот, что не годится данный метод доказательства - индукция.
Теперь попробуем доказать тем же методом неравенство
Т.к. это неравенство более сильное, то, казалось бы, и доказывать его не имеет смысла, ведь придем к тому же. Однако, попробуем.
База опять очевидна.
Проводя доказательство так же, сначала получим
и
Останется доказать, что
Аналогичным образом возведем в квадрат и раскроем скобки; получим
4k3 + 12k2 + 9k + 2 <= 4k3 + 12k2 + 12k + 4
И что же мы видим? Неравенство истинно. Следовательно, и исходное (то, которое более сильное) тоже верно!
Эта ситуация, когда доказать более сильное утверждение легче, чем более слабое, и называется парадоксом изобретателя. Он был известен еще и древним мыслителям, но придумал это название в начале XX века венгерский математик Д. Пойа, сказав о парадоксе следующие слова: "Легче доказать более сильную теорему, чем более слабую". Этот парадокс существует не только в математике, но и в других областях, в том числе и в жизненных ситуациях. Такое же название (и по праву) получили ситуации, когда решить более общую задачу легче, чем более узкую. Прием, позволяющий это сделать, заключается в том, чтобы свести задачу к более общей, относительно которой исходная задача будет являться лишь частным случаем. Приведу один пример:
В III веке до н. э. тиран города Сиракузы Гиерон поручил своему подданному и близкому родственнику Архимеду определить, не подмешано ли к его золотой короне, изготовленной ювелирами, менее благородное серебро. Эту частную задачу Архимед смог решить лишь как общую (т.к. о химическом анализе тогда еще и не помышляли; к тому же корону разрушать было нельзя), выявив закон "подъемной силы", то есть силы Архимеда, действующей на погруженное в жидкость тело.
Таким же образом появились на свет в математике интегральное (выросшее из изобретенного древнегреческим математиком Евдоксом Книдским (около 408 - около 355 до н. э.) метода "исчерпывания") и дифференциальное (когда Лейбниц Готфрид Вильгельм (1646 - 1716) долго бился на задачей проведения касательной к кривой в заданной точке, сведя ее к проведению секущей через две бесконечно близкие точки) исчисления, в науке изобретена пастеризация и многое-многое другое.
Вывод
Софизмом называется умышленно ложное умозаключение, которое имеет видимость правильного. Каков бы ни был софизм, он обязательно содержит одну или несколько замаскированных ошибок.
Разбор софизмов, прежде всего, развивает логическое мышление, т.е. прививает навыки правильного мышления. Обнаружить ошибку в софизме - это значит осознать ее, а осознание ошибки предупреждает от повторения ее в других математических рассуждениях. Помните, что важно добиться отчетливого понимания ошибок, иначе софизмы будут бесполезны.
Литература
1. Ахманов А. С. Логическое учение Аристотеля
2. Брадис В. М., Минковский В. Л., Харчева Л. К. «Ошибки в математических рассуждениях»
3. Пельман Я. И. «Занимательная математика»
4. В. А. Кордемский, А. А. Ахадов «Удивительный мир чисел» Математический словарь