Решение.
а)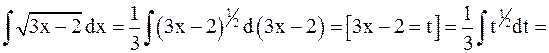 
;
б) 
;
в) 
.
Пример 3. Найти 
.
Решение. 
.
Этот пример можно решить ещё и так:
, 
;
;
Пример 4. Найти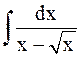 
.
Решение. Положим 
.
Тогда 
и
.
Пример 5. Найти 
.
Решение. Применим подстановку 
.
Тогда 
.
Имеем 
.
5. Интегрирование по частям
Если u(x), v(x) дифференцируемы, то справедлива формула интегрирования по частям
.
Эту формулу следует применять в тех случаях, когда подынтегральное выражение vdu проще исходного выражения udv.
Ниже приведены основные типы интегралов, берущихся по частям.
| I тип | II тип | III тип (интегралы, приводящиеся к себе) |
| 
| 
|
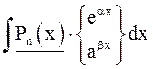
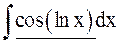
За u принимаются подчёркнутые функции, за dv – остальная часть подынтегрального выражения. Pn (x) – многочлен степени n. Интегралы I типа берутся путём интегрирования по частям n раз, II типа – m раз, III типа (за исключением двух последних) – 2 раза (причём, в первом интеграле III типа оба раза за u можно принять как 
, так и тригонометрические функции 
, 
).
По частям могут быть взяты и интегралы, не вошедшие в эту таблицу.
Пример 6. Найти интегралы:
а) 
; б) 
; в) 
.
Решение. а) 
.
Здесь и ниже при нахождении v при известном dv мы полагаем С = 0 (как в этом случае: dv = dx, отсюда следует v = x + C, но мы берём одну из первообразных v = x).
б) 
.
в) Обозначим 
. Имеем
.
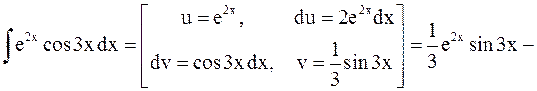
Получается, что 
Отсюда находим (учитывая, что J является семейством функций, отличающихся друг от друга на постоянную величину)
.
Интегрирование рациональных функций
Интегрирование рациональной функции
, 
, являющейся правильной дробью (т.е. при 
), производится путём представления этой функции в виде суммы простых дробей. Если же дробь является неправильной (
), то её представляют в виде суммы многочлена и правильной дроби, затем интегрируют эти слагаемые.
Пример 7. Найти интегралы: а) 
; б) 
.
Решение. а) 
Иногда 
вычисляют иначе
б)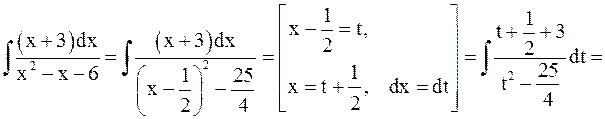 
.
Пример 8. Найти интегралы: а) 
;
б) 
; в) 
.
Решение. а) Найдём разложение подынтегральной функции 
на сумму простых дробей:
;
;
;
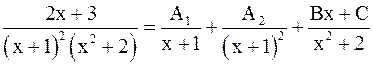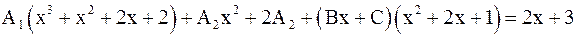Таким образом, 
.
б) 
.
Разложим подынтегральную функцию 
на сумму простых дробей:
;
. (1)
x = 0; –8A = +5. Þ A = –5/8,
x = 2; 24B = 3. Þ B = 1/8.
Из равенства (1) следует (приравниваются коэффициенты при x3 и x):
Отсюда, зная уже A = –5/8, B = 1/8, находим C = 1/2, D = 7/4. Таким образом, 
.
в) Рациональная функция 
представляет собой неправильную дробь. Выделим целую часть делением уголком
x4 – 3x2 + 2x +7 x3 – 2x2 + x
x4 – 2x3 + x2 x + 2
2x3 – 4x2 + 2x + 7
2x3 – 4x2+2x
Таким образом,
.
Разложим правильную дробь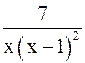 
на сумму простых дробей:
;
; (2)
x = 0; A = 7;
x = 1; B2 = 7.
Сравнивая старшие коэффициенты в обеих частях равенства (2), находим A + B1 = 0, B1 = –A = –7. Таким образом,
.
7. Интегрирование тригонометрических функций
При интегрировании функций вида 
лучше придерживаться следующего правила: 1) если n нечётное положительное число, то делаем замену переменной 
если m – нечётное положительное число, то делаем замену переменной 
и это приведёт к интегралу от степенной функции; 2) если n и m – чётные числа, то с помощью формул 
, 
достигается упрощение вида подынтегральной функции.
Пример 9. Найти а) 
; б) 
.
Решение. 
= 
= 
;
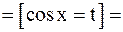
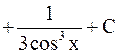б) 
.
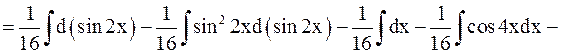
Интегрирование функций вида 
, 
, 
производится с помощью формул произведений синусов и косинусов.
Пример 10. Найти 
.
Решение. 
.
Интегрирование функций вида R(sinx, cosx), где R – рациональная функция двух переменных, производится с помощью замены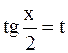 
. При этом 
, 
, 
,
.
Пример 11. Найти 
.
Решение. = 
=
.
8. Интегрирование некоторых иррациональных функций
Интегралы вида 
, где R – рациональная функция двух переменных, выделением полного квадрата приводятся к одному из следующих видов:
1) 
; 2) 
; 3) 
.
Эти последние интегралы находятся с помощью подстановок:
1) t = a tgu или t = a shu; 2) t = a/cosu или t = a chu;
3) t = a sinu или t = a thu.
Пример 12. Найти 
.
Решение. = 
=
= 
.
Пример 13. Найти 
.
Решение. = 
= 
.
Пример 14. Вычислить 
.
Решение.
.
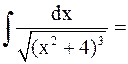
9. Определённый интеграл
Пусть функция f(x) определена на отрезке [a, b]. Разобьём этот отрезок точками 
на n частей [x k-1; xk], 
; обозначим 
. Число 
, , назовём диаметром разбиения. Возьмём в каждом частичном отрезке [xk-1; xk] по точке tk и образуем следующую сумму, называемую интегральной:
.
Если существует конечный предел интегральных сумм при 
, предел, не зависящий ни от способа разбиения отрезка [a; b], ни от выбора точек 
, то функция f(x) называется интегрируемой на [a; b], а сам предел – определённым интегралом от f(x) на [a; b] и обозначается 
.
По определению положим
= 
, 
.
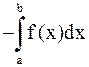Если f(x) непрерывна на [a; b], то она интегрируема на [a; b].
К интегрируемым функциям относятся также:
1) монотонно возрастающие (убывающие) и ограниченные на [a; b];
2) ограниченные и имеющие лишь конечное число точек разрыва на
[a; b].
Определённый интеграл обладает следующими свойствами:
1) если f(x) интегрируема на большем из отрезков [a; b], [b; c], [a; c], то f(x) интегрируема и на двух других и при этом
= + 
;
2) если f(x) и g(x) интегрируемы на [a; b], то 
также интегрируема на [a; b] и при этом
= 
+ 
;
3) если 
интегрируема на [a; b], то f(x) также интегрируема на
[a; b] и при этом 
;
4) если f(x) и g(x) интегрируемы на [a; b] и f(x) £ g(x) 
, то
;
5) если f(x) интегрируема на [a; b] и m £ f(x) £ M , то 
.
Теорема 2. Если F(x) – первообразная функции f(x), непрерывной на [a; b], то
(формула Ньютона–Лейбница).
Разность 
часто обозначают 
.
Пример 15. Найти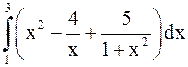 
.
Решение.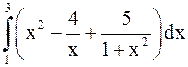 
.
Теорема 3. Пусть f(x) непрерывна на [a; b] и функция 
удовлетворяет следующим условиям: 1) 
дифференцируема на 
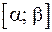; 2) 
, 
; 3) значения не выходят за пределы
[a; b], когда t пробегает значения из 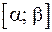. Тогда
.
Пример 16. Вычислить 
.
Решение. 1) Функция 
непрерывна на интервале [3,6].
2) Применим подстановку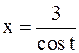 
и изменим пределы интегрирования. Если 
, то 
и 
. Если 
, то 
и 
.
Отметим, что функция 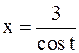удовлетворяет на отрезке 
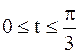условиям теоремы о замене переменной в определенном интеграле, так как она непрерывно дифференцируема, монотонна и 
и 
.
3) 
, 
,
так как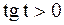 
при .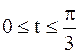
.
Пример 17. Вычислить: а)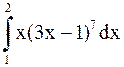 
; б)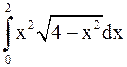 
.
Решение. а) Сделаем замену переменного: 
. Тогда 
; 
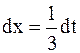; меняются пределы интегрирования: 
, 
.
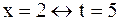Имеем 
.
б) 
.
Теорема 4. Если u(x), v(x) дифференцируемы на [a; b], то
.
Пример 18. Вычислить 
.
Решение. 
.
10. Несобственные интегралы
1. Несобственный интеграл I рода. Пусть функция f(x) определена на 
и интегрируема на отрезке [a; b] для любого 
. Несобственный интеграл первого рода определяется равенством
.
Если существует конечный предел в этом равенстве, то интеграл называется сходящимся, в противном случае – расходящимся. Аналогично определяются несобственные интегралы
и 
:
, 
.
Пример 19. Вычислить: а) 
; б) 
; в) 
.
Решение.
а) 
.
б) 
,
и интеграл расходится;
в) 
.
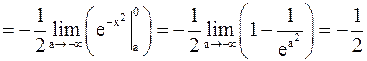Несобственный интеграл I рода обладает свойством линейности:
(при условии сходимости интегралов в правой части равенства).
Для исследования вопроса сходимости несобственного интеграла часто оказывается полезным следующий факт: пусть 
, тогда:
Аналогичное утверждение справедливо для интеграла 
, 
, и 
, a > c.
Теорема 5 (первый признак сходимости). Пусть f(x) и g(x) определены на , для любого b>a f(x), g(x) интегрируемы на 
и 
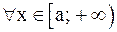. Тогда имеем:
1) если 
сходится, то сходится и 
;
2) если расходится, то расходится и .
Теорема 6 (второй признак сходимости). Пусть f(x) и g(x) определены на , 
и пусть существует конечный предел 
. Тогда интегралы , ведут себя одинаково в смысле сходимости (т.е. одновременно сходятся или расходятся).
Теорема 7. Если 
сходится, то сходится и
(в таком случае говорят, что сходится абсолютно).
Аналогичные утверждения справедливы для несобственного интеграла .
Пример 20. Исследовать на сходимость интегралы:
а) 
; б) 
; в) 
.
Решение. а) Подынтегральная функция 
представляет собой рациональную функцию, разность степеней числителя и знаменателя равна 2. Рассмотрим вспомогательную функцию 
. Найдём предел
.
Следовательно, согласно второму признаку сходимости, интегралы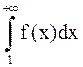 
и 
ведут себя одинаково в смысле сходимости. Но известно, что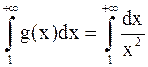 
сходится 
, значит и наш интеграл 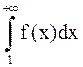сходится.
б) 
является иррациональной функцией; степень числителя равна 3/2 (числитель можно представить как 
), степень знаменателя равна 2. Рассмотрим вспомогательную функцию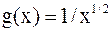 
. Докажем, что существует конечный предел 
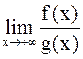, не равный 0. Действительно,
.
Поэтому 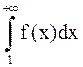, ведут себя одинаково в смысле сходимости. А так как 
расходится, то расходится и .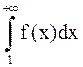
в) Обозначим 
. Так как 
, то 
. Интеграл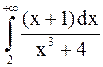 
сходится (доказывается это, как и выше: 
, 
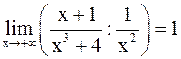сходится и можно воспользоваться вторым признаком сходимости). Мы попадаем в условие теоремы 5 (часть 1), в которой говорится, что наш интеграл сходится.
2. Несобственный интеграл II рода. Пусть функция f(x) определена на [a; b) и 
(или = – ¥). Несобственный интеграл второго рода функции f(x) на [a; b] определяется равенством
.
Если существует конечный предел в этом равенстве, то говорят, что интеграл сходится, в противном случае – расходится. Аналогично определяется несобственный интеграл II рода для случаев 
и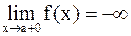 
. Если же f(x) неограниченна в любой окрестности некоторой внутренней точки 
, то полагают
.
Пример 21. Вычислить интегралы: а) 
; б) 
.
Решение. а)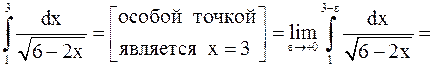 
.
б) 
.
Значит, интеграл расходится.
Формулировки признаков сходимости для несобственных интегралов II рода, по существу, ничем не отличаются от формулировок признаков сходимости для несобственных интегралов I рода. Для применения этих признаков полезно пользоваться тем, что
, 
Пример 22. Исследовать на сходимость интегралы:
а) 
; б) 
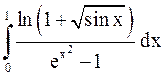; в) 
.
Решение. а) 
. Подынтегральная функция 
в промежутке [2; 3] имеет особую точку x = 2. Множитель 
стремится к 1/2 при 
. Поэтому естественно ожидать, что наша функция в окрестности точки x = 2 ведёт себя, как 
; проверим это:
.
Следовательно, согласно второму признаку сходимости, интегралы 
и 
ведут себя одинаково в смысле сходимости. Но второй интеграл сходится (p = 1/2 < 1), поэтому сходится и наш интеграл.
б) Функция 
имеет на промежутке [0; 1] одну особую точку x = 0. Функции 
и 
являются бесконечно малыми величинами при 
. Известно, что ~ 
~ 
, ~ x2 при . Поэтому ~ 
при 
. А так как 
расходится 
, то расходится и наш интеграл.
в) Разложим знаменатель (
) подынтегральной функции 
по формуле Тейлора в окрестности особой точки 
функции :
.
Следовательно, 
~ 
~ 
.
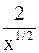Известно, что 
сходится, следовательно, сходится и наш интеграл.
11. Вычисление площадей плоских фигур
Площадь криволинейной трапеции, ограниченной графиками функций x = a, x = b, y = 0, y = f(x) (f(x) ³ 0 при x Î [a; b]), находится по формуле 
.
Если фигура (D) ограничена графиками функций x = a, x = b, y = f(x), y = g(x), f(x) ³ g(x) при xÎ [a; b], то площадь S фигуры (D) находится по формуле 
.
Пример 23. Найти площадь S фигуры (D), ограниченной линиями y = –x2 + 2x + 2 и y = 2x + 1.
Решение. Найдём абсциссы точек пересечения графиков функций, для чего решим уравнение: –x2 + 2x + 2 = 2x + 1; x2 – 1 = 0; x1 = –1,
x2 = 1. Для всех точек x из отрезка [–1; 1] –x2 + 2x + 2 ³ 2x + 1. Поэтому
.
Пример 24. Найти площадь фигуры, ограниченной эллипсом 
.
Решение. Эллипс имеет две оси симметрии: координатные оси 0х и 0у. Поэтому площадь S фигуры равна учетверённой площади S1 части (D1) фигуры, расположенной в первой четверти (заштриховано). Фигура (D1) ограничена сверху линией 
, снизу – осью 0х, слева – осью 0у. Поэтому
.
Отсюда находим S = 4S1 = pab.
Площадь S криволинейного сектора, ограниченного графиком функции 
и лучами 
и 
в полярной системе координат, находится по формуле 
.
Пример 25. Найти площадь S фигуры, ограниченной линией, заданной в полярной системе координат уравнением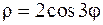 
.
Решение. Начнём с изображения линии. Так как 
, то нам нужно сначала решить неравенство 
. Имеем
, 
, 
.
При n = 0: 
;
при n = 1: 
;
при n = 2: 
;
при n = 3: 
– этот угол является повторением угла, соответствующего значению n = 0. Рассмотрение других значений приводит к уже полученным углам на плоскости. Рассмотрим рисунок. Наша фигура ограничена тремя лепестками. Её площадь S равна 3S1, где S1 – площадь одного лепестка (заштриховано).
Имеем
.
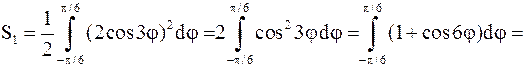
Отсюда находим S = 3S1= p.
12. Вычисление длины дуги
Линия (L) в пространстве называется гладкой, если в каждой точке (L) можно провести касательную к этой линии. Если линия без самопересечений задана параметрическими уравнениями
то дифференцируемость x(t), y(t), z(t) гарантирует гладкость линии; аналогичное утверждение справедливо для плоской линии. Если линия без самопересечений на плоскости с заданной полярной системой координат определена полярным уравнением 
, то и в этом случае дифференцируемость 
влечёт гладкость этой линии.
Если гладкая линия (L) на плоскости (в пространстве) задана параметрическими уравнениями 
, 
(и вдобавок к этому 
для линии в пространстве), 
, то длина 
линии (L) находится по формуле
(
).
Если гладкая линия (L) задана явным уравнением 
, 
, то 
.
Для гладкой линии (L), заданной полярными уравнениями, , 
.
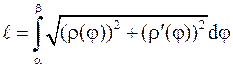Пример 26. Найти длину линии, заданной уравнением 
, 
, 
.
Решение. Имеем 
.
Пример 27. Найти длину дуги логарифмической спирали 
, находящейся внутри окружности 
.
Решение. Дуге спирали, лежащей внутри окружности , соответствуют значения 
. Поэтому
.
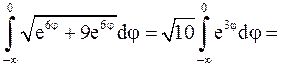
13. Вычисление объёмов тел
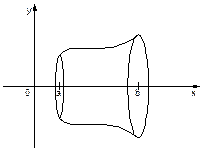Если в пространстве заданы ось 0х, тело (Т), проекцией которого на 0х является отрезок [a; b], и для любого x Î [a; b] известна площадь S(x) поперечного сечения S(x), то объём V тела (Т) находится по формуле
.
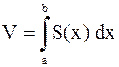В частности, если тело (Т) получено путём вращения графика функции 
, 
вокруг оси 0х, то объём тела вращения равен 
.
При вращении графика функции f(x) вокруг оси 0у формула объёма принимает вид
.
Пример 28. Найти объём V тела (Т), ограниченного эллипсоидом
.
Решение. Проекцией тела (Т) на ось 0х является отрезок [–a; a]. Найдём формулу площади S(x) поперечного с