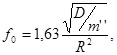(1.4)
где R – радиус пластины, м; D = 0,09Eh3 – жесткость пластины,
Н·м; m'' = 0,318m/R2 – распределенная по площади массы пластины m.
Величина прогиба Zmax, м, и частота собственных колебаний элемента конструкции f0, Гц, связаны формулой Гейгера:
Повышение прочности можно достичь, используя ребра жесткости, которые должны крепиться не только к пластине, жесткость которой они повышают, но и к опорам конструкции.
Для прямоугольной пластины, свободно опертой по контуру и имеющей ребра жесткости, параллельные осям координат.
(1.6)
где а в – длина и ширина пластины, м; а х, hx – параметры сечения ребра, параллельного оси Х, м; Вх, By – жесткости ребер, параллельных осям соответственно X и Y, Н·м,
Bx = 0,09E a xhx3; By = 0,09E в yhy3;
Mx, My – масса ребер; r, K – число ребер, параллельных осям соответственно X и Y; mn – масса пластины, кг; n, m – число полу волн в направлении осей X и Y; D – цилиндрическая жесткость пластины, Н·м.
Если ребра, параллельные оси Y отсутствуют, то
(1.7)
Расчет элементов на прочность следует проводить исходя из основных соотношений теории сопротивления материалов:
при растяжении – сжатии
σр–сж = р/s ≤ [ σ ]р–сж ;
при срезе
tср = р/s ≤ [ t ]ср ;
при изгибе
σи = Мu / W < [ σ]u ;
при кручении
tкр = Мкр / Wp ≤ [ t ]кр,
где Р – усилие действующее на деталь, Н; S – площадь сечения детали, м2; Mu, Mкр – изгибающии и крутящии моменты, Н·м; W, Wp – моменты сопротивления при изгибе и кручении, м3 .
Таким образом, определение нагрузок сводится к определению сил и моментов, действующих на деталь.
Нагрузки статистического режима:
а) сила тяжести P, H:P = mg, где m – масса элемента, кг; g – ускорение свободного падения g = 9,8 м/с2
|
|
б) сумма систем сил (равнодействующая),
в) момент силы, Н·м; Mp = Ph;
г) сумма моментов сил, Н·м:
д) момент сопротивления сечения W;
е) момент инерции сечения I.
Нагрузки при вибрациях
P = mgηnn(1.8)
где m – масса детали с учетом массы элементов, закрепленных на ней, кг; g – ускорение свободного падения, м/с2; nn – вибрационная перегрузка, действующая на деталь при резонансе; η – коэффициент динамичности, позволяющий привести задачу к статической,
(1.9)
здесь δ0 – параметр, пропорциональный коэффициенту демпфирования β,
(1.10)
К – жесткость элемента, Н/м, К = 4π2f02m; f – частота вибраций, Гц; f0 –частота собственных колебаний элемента, Гц.
В околорезонансной области частот
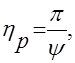(1.11)
где ψ – логарифмический декремент затухания.
Нагрузки при ударах если принять форму ударного импульса прямоугольной, длительностью τ, то ударную нагрузку можно определить по формуле
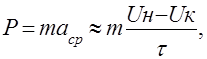(1.12)
где Uн – начальная скорость элемента конструкции при ударе; Uк – конечная скорость элемента конструкции при ударе.
Начальную скорость обычно находят из равенства потенциальной и кинетической энергий, например при падении РЭА с высоты
Скорость в конце удара определяется коэффициентом восстановления К в.
Тогда выражение (1.12) принимает вид
(1.13)
Для более сложных форм ударных импульсов необходимо определить спектр воздействующих частот и рассчитать ударную нагрузку как взвешенную сумму спектральных составляющих.
|
|
Для моделей типа балок и пластин при падении конструкции ударная перегрузка
(1.14)
где Н – высота падения, м; Zmax – максимальный прогиб детали, м.
В качестве допускаемых параметров прочности обычно принимают допускаемые механические напряжения в конструкциях.
Допускаемые механическим напряжением называется такое безопастное напряжение, которое деталь может выдержать в течение заданного срока эксплуатации.
Допускаемое напряжение при расчете деталей на прочность определяется по формулам:
[ σ ] = σпред/n и [ t ] = tпред/n,
где σпред, tпред – продельные значения механических напряжений; n – запас прочности.
Определение запаса прочности при статических нагрузках. При постоянных напряжениях, возникающих при статических нагрузках, прочность хрупкого материала и материала с низкой пластичностью определяется приделом прочности σпред = σв, а пластичного – приделом текучести σпред = σт.
Запас прочности устанавливают в виде произведения частных коэффициентов:
n = n1n2n3, (1.15
где n1 – коэффициент достоверности определения расчетных нагрузок и напряжений; при повышенной точности n1 = 1,2 – 1,5; для оценочных расчетов n1 = 2 – 3; n2 –коэффициент, учитывающий степень ответственности детали, обусловливающий требования к надежности; для мало ответственных и не дорогих деталей n2 = 1 – 1,2, если поломка детали вызывает отказ – n2 =1,3, аварию – n2 =1,5; n3 – коэффициент, учитывающий однородность механических свойств материалов, который при статических нагрузках следует выбирать в зависимости от степени пластичности материала (σт/σ в): при σт/σ в = 0,49 – 0,55 коэффициент n3 =1,2 – 1,5; при σт/σ в = 0,55 – 0,70 n3 =1,5 – 1,8; при σт/σ в = 0,7 – 0,9 n3 =1,8 – 2,2. Для деталей, отлитых из пластмасс, n3 =1,6 – 2,5; для хрупких однородных материалов n3 = 3 – 4; для хрупких неоднородных материалов n3 = 4 – 6. При переменных нагрузках для однородных материалов и высокоточных технологий n3 = 1,3 – 1,5, для среднего уровня технологии n3 = 1,5 – 1,7; для материалов пониженной однородности n3 = 1,7 – 3.
|
|
Прочность при цилиндрических нагрузках. В процессе эксплуатации на детали ботовой, морской, возимой и носимой РЭА в большинстве случаев действуют нагрузки, циклически изменяющиеся по частоте и амплитуде. Следовательно, в них возникают различные циклические напряжения. Необходимо различать следующие основные циклы напряжений:
1) симметричный знакопеременный, когда наибольшие и наименьшие напряжения противоположны по знаку и одинаковы по значению;
2) асимметичный знакопеременный, когда наибольшие и наименьшие напряжения противоположны по знаку и неодинаковы по значению;
3) пульсирующий, когда напряжения изменяются от нуля до максимума.
Придел выносливости для симметричных циклов обозначают индексом (–1), для пульсирующих – индексом (0).
Приделы выносливости на изгиб с симметричным циклом:
для стального проката σпред = σ-1=(0,2 –0,3)σв(1+ σ0,2/σ в), где σ0,2 – условный придел текучести при статическом растяжении;
для стального литья и медных сплавов σпред = σ-1=(0,3 –0,4)σв;
для алюминиевых и магнитных сплавов σпред = σ-1=(0,3 –0,6)σв;
Приделы выносливости при симметричном цикле связаны ориентировочной зависимостью:
t-1 = (0,5 – 0,7)σ-1.
Приделы выносливости при пульсирующем и знакопеременном симметрических циклах связаны зависимостями:
при изгибе σпред = σ ≈ (1,4 – 1,6)σ-1;
при растяжении σпред = σ0 ≈ (1,5 – 1,8)σ-1(1.16)
Эти зависимости справедливы для деталей, длительное время работающих при циклических нагрузках (свыше 107 циклов).
Если вибрация или удары носят кратковременный характер, допускаемое напряжение при N циклах
σN = σ-1 + 0,167 (σT – σ-1) (в – lgN) (1.17)