Таблица 1
Исходные данные по некоторым ресурсам и технологическим коэффициентам для задачи ДЗ
| Виды ресурсов, норм и т.д., Единицы измерения | Нормативные коэффициенты для различных отраслей хозяйства | Ресурсы хозяйства | |||
| Производ-ство зерна | Скотовод-ство | Свиновод-ство | Производ-ство кормов | ||
| Трудозатраты чел. ч./га, чел. ч./гол. | чел.ч | ||||
| Ден. Затраты тыс.руб/га тыс.руб/гол | тыс.руб | ||||
| Урожайность, ц.к.е./га | |||||
| Нормы кормления, ц.к.е./гол: Общая Концентра-ты | |||||
| Продуктив-ность (за год) л/гол кг/гол | |||||
| Чистый доход,тыс.руб/ц.к.е. тыс.руб/л тыс.руб/кг | 0,2 |
Целевая функция – суммарный чистый доход от всех видов товарных отраслей. При формировании целевой функции необходимо учесть размерность соответствующих нормативных коэффициентов (последняя строка табл.1), долю зерна на продажу (0,9), урожайность зерна и продуктивность животных. В итоге получим:
Z = 10*0,9*25*X1 + 0,2*4000*X2 + 1*100*X3 = 225*X1 +800*X2 + 100*X3.
Построим систему ограничений.
1. ограничение по площади пашни (учитываются все культуры, под которые отводится пашня).
Х1 + Х4  900
900
2. ограничение по трудовым ресурсам.
В соответствии с нормами трудозатрат (первая строка табл.1) имеем:
5*Х1 + 50*Х2 + 100*Х3 + 50*Х4  40000
40000
3. ограничение по денежным ресурсам.
Х5  90000
90000
4. ограничение по кормовому балансу.
Общий вид ограничения таков:
“потребность в кормах”  “производство кормов”
“производство кормов”
При записи ограничений должны быть учтены нормы кормления, урожайность кормовых культур, доля зерна (0,1), используемого на фураж.
Конкретные ограничения составляются следующим образом.
По всем видам животных:
80*Х2 + 40*Х3  0,1*25*Х1 + 50*Х4 + 1000
0,1*25*Х1 + 50*Х4 + 1000
Последнее слагаемое в правой части неравенства учитывает тот факт, что на корм коровам используется не только урожай с пашни, но и корма с пастбищ и сенокосов.
По концентратам:
30*Х2 + 10*Х3  2,5*Х1
2,5*Х1
В правой части этого неравенства используется только переменная Х1, т.к. здесь должны быть учтены только концентрированные корма.
5. Отдельно по коровам (по всем видам кормов):
80*Х2  2,5*Х1 + 50*Х4 + 1000
2,5*Х1 + 50*Х4 + 1000
6. Отдельно по свиньям (по всем видам кормов):
40*Х3  2,5*Х1 + 50*Х4
2,5*Х1 + 50*Х4
7. Ограничение по поголовью коров:
Х2  110
110
8. Ограничение по гарантированному производству свинины:
100*Х3 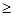 3000
3000
9. Уравнение для расчета общих денежных затрат (см. вторую строчку табл. 1):
70*Х1 + 25*Х2 + 100*Х3 + 300*Х4 = Х5
Анализируя полученные ограничения, нетрудно заметить, что неравенство, определяющее баланс всех видов кормов по коровам является избыточным, ибо автоматически выполняется при выполнении аналогичного более жесткого ограничения по всем видам животных. Следовательно, в дальнейшем оно может быть исключено из рассмотрения. По тем же причинам мы не составляли ограничения по концентратам отдельно по коровам и свиньям.
С учетом всего сказанного получим следующую систему ограничений:
Х1 + +Х4  900 (1)
900 (1)
5*Х1 + 50*Х2 + 100*Х3 + 50*Х4  40000 (2)
40000 (2)
Х5  90000 (3)
90000 (3)
-2,5*Х1 + 80*Х2 + 40*Х3 - 50*Х4  1000 (4)
1000 (4)
-2,5*Х1 + 30*Х2 + 10*Х3  0 (5)
0 (5)
-2,5*Х1 + + 40*Х3 – 50*Х4  0 (6)
0 (6)
Х2  110 (7)
110 (7)
100*Х3 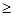 3000 (8)
3000 (8)
70*Х1 + 25*Х2 + 100*Х3 + 300*Х4 = 0 (9)
Добавим к этой системе требование, накладываемое на целевую функцию:
Z = 225*Х1 + 800*Х2 + 100*Х3 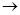 max, (10)
max, (10)
и условия неотрицательности переменных:
Х 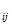
 0, j = 1,…,5. (11)
0, j = 1,…,5. (11)
В совокупности соотношения (1) … (11) образуют развернутую математическую формулировку общей задачи линейного программирования в неканоническом представлении. В обобщенном виде та же задача записывается по следующей схеме:
Z = 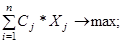
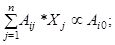 i=1,…,m,
i=1,…,m,
где m – общее число ограничений; n – общее число основных переменных, а символ 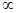 означает либо “
означает либо “  ” либо “
” либо “ 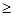 ” либо “ = ”.
” либо “ = ”.
Общую развернутую запись задачи, оформленную в виде таблицы, называют математической моделью задачи. Табличная форма это наиболее удобное представление задачи при работе на ЭВМ (см. табл. 2).
Таблица 2
Математическая модель задачи ДЗ
(неканоническое представление)
| Основные переменные и ограничения | Х1 | Х2 | Х3 | Х4 | Х5 | тип ограни-чений | правые части ограничений |
| 1. ресурс пашни | 
| ||||||
| 2. трудовые ресурсы | 
| ||||||
| 3. денежные ресурсы | 
| ||||||
| 4. баланс кормов | -2.5 | -50 | 
| ||||
| 5. баланс концентр-в | -2.5 | 
| |||||
| 6. баланс кормов(свиньи) | -2.5 | -50 | 
| ||||
| 7. поголовье коров | 
| ||||||
| 8. производство свинины | 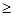
| ||||||
| 9. денежные затраты | -1 |  = =
| |||||
| коэффициенты целевой функции | 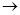 max max
|
Приведение задач линейного программирования к каноническому представлению.
Приведение задач к каноническому виду (т.е. приведение ограничений к типу " - ") осуществляется за счет использования неотрицательных дополнительных переменных, вводимых в ограничения, и, частично, в целевую функцию.
Вначале каждому ограничению типа нестрогого неравенства "  " или "
" или " 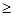 " сопоставим свою дополнительную переменную. Проделаем это следующим образом.
" сопоставим свою дополнительную переменную. Проделаем это следующим образом.
В ограничениях типа " 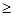 " вычтем из левой части дополнительную переменную, а в ограничениях типа "
" вычтем из левой части дополнительную переменную, а в ограничениях типа "  " прибавим к левой части дополнительную переменную, при этом все знаки нестрогого неравенства заменим на равенства. Каков смысл этих действий?
" прибавим к левой части дополнительную переменную, при этом все знаки нестрогого неравенства заменим на равенства. Каков смысл этих действий?
Рассмотрим, например, процесс такого изменения для 8-го неравенства - типа " 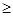 " (соответствующую дополнительную переменную обозначим Х6). В результате придем к следующему представлению ограничения:
" (соответствующую дополнительную переменную обозначим Х6). В результате придем к следующему представлению ограничения:
100*Х3 – Х6 =3000
Величина Х6 в этом равенстве называется избыточной переменной. Ее значение показывает, насколько левая часть исходного неравенства (8) превышает правую, а с экономической точки зрения Х6 означает сверхплановое производство свинины:
Х6 = 100*Х5 - 3000
Именно в этом смысл термина "избыточная переменная".
От 1-го неравенства (типа " 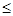 "), введя дополнительную переменную Х7, придем к следующему ограничению:
"), введя дополнительную переменную Х7, придем к следующему ограничению:
X1 + Х4 * Х7 = 900
Величина Х7 в этом равенстве называется остаточной переменной. Ее значение показывает, насколько левая часть исходного неравенства (1) меньше правой:
X7 = 900 – X1 – X4,
то есть в данном случае, какая часть пашни остается неиспользованной. Именно в этом смысл термина "остаточная переменная".
Помимо избыточных и остаточных переменных в левые части ограничения типа " 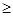 " и " = " вводят со знаком " + " еще дополнительные неотрицательные переменные, называемые искусственными.
" и " = " вводят со знаком " + " еще дополнительные неотрицательные переменные, называемые искусственными.
Итак, в результате придем к следующей канонической системе ограничений (вформе уравнений):
Х1 + +Х4 + Х7 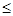 900 (1)
900 (1)
5*Х1 + 50*Х2 + 100*Х3 + 50*Х4 + Х8 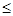 40000 (2)
40000 (2)
Х5 + Х9 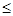 90000 (3)
90000 (3)
-2,5*Х1 + 80*Х2 + 40*Х3 - 50*Х4 + Х10 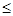 1000 (4)
1000 (4)
-2,5*Х1 + 30*Х2 + 10*Х3 + Х11 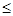 0 (5)
0 (5)
-2,5*Х1 + + 40*Х3 – 50*Х4 + Х12 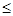 0 (6)
0 (6)
Х2 + Х13 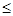 110 (7)
110 (7)
100*Х3 - Х6 + Х14 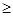 3000 (8)
3000 (8)
70*Х1 + 25*Х2 + 100*Х3 + 300*Х4 Х15 = 0 (9)
в которой X1,...,X5 - основные, Х6 - избыточная, Х7, …,Х13, - остаточные и Х14, Х15 – искусственные переменные.
Предыдущие пояснения показывают, каков экономический смысл дополнительных переменных. С вычислительной точки зрения их введение позволяет сразу получить первое (опорное) решение задачи. Действительно, если основные и избыточные переменные положить равными нулю, то из ограничений будет сразу следовать, что остаточные и искусственные переменные должны быть равны правым частям соответствующих ограничений.
Уравнение целевой функции:
Z = 225*Х1 + 800*Х2 + 10*Х3 – М*Х14 – М*Х15 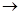 max,
max,
где М – большое число (больше остальных коэффициентов целевой функции).
Таблица 3
Последняя симплекс-таблица задачи ДЗ
(Zmах = 240538)
| Номер строки | Базисные переменные | Номера ограничений для дополнительных переменных | Аiо | Коэффициенты замещения | |||
| Аi6(X6) (изб.огр.8) | Аi7(X7) (ост.огр.1) | Аi10(X10) (ост.огр.4) | Аi11(X11) (ост.огр.5) | ||||
| Х12(ОСТ) | 0,2831 | 6,15 | -0,877 | 2,338 | |||
| Х8(ОСТ) | 0,86 | -10 | 0,2 | -2,2 | |||
| Х9(ОСТ) | 1,478 | -89,62 | 4,208 | -12,05 | |||
| Х2(ОСН) | - | 60,15 | 0,0035 | 0,0769 | 0,0015 | 0,029 | |
| Х3(ОСН) | - | -0,01 | |||||
| Х1(ОСН) | - | 841,8 | 0,0025 | 0,923 | 0,0184 | -0,049 | |
| Х13(ОСТ) | 69,85 | -0,0035 | -0,077 | -0,015 | -0,029 | ||
| Х5(ОСН) | - | -1,478 | 89,62 | -4,2 | 12,05 | ||
| Х4(ОСН) | - | 58,15 | -0,0025 | 0,0769 | -0,018 | 0,049 | |
| (Zj – Cj) | 2,385 | 269,2 | 5,385 | 12,31 |
К основным блокам информации относятся:
1). Собственно оптимальное решение - значения переменных, попавших в число базисных (см. 2-й и 4-й столбцы табл. 3). Напомним, что небазисные переменные равны нулю.
2). Значения целевой функции, которое дается начальным элементом индексной строки - (Z0-C0), расположенным на пересечении столбца Аi0 и строки (Zj-Cj). В данном случае оно равно 240538.
3). Значения элементов индексной строки, соответствующих остаточным и избыточным переменным. Эти значения называют двойственными оценками или, точнее, оценками переменных двойственной задачи линейного программирования. Напомним, что если переменная попала в число базисных, то соответствующий ей элемент индексной строки равен нулю.
4). Коэффициенты замещения.