ЛАБОРАТОРНАЯ РАБОТА N 6
АНАЛИЗ ПОЛЯРИЗАЦИИ ЛАЗЕРНОГО СВЕТА
ЦЕЛЬ РАБОТЫ
1.1. Изучить типы поляризации света и методы их описания.
1.2. Ознакомиться с методикой анализа поляризации света.
1.3. Провести анализ поляризации лазерного излучения.
1.4. Определить угол Брюстера и показатель преломления стекла на длине волны излучения лазера.
ПОЛЯРИЗАЦИЯ СВЕТА
Естественный и поляризованный свет.
Свет, в котором направления колебаний вектора E упорядочены каким либо образом, называется поляризованным.
Волна называется линейно поляризованной (или иначе плоско поляризованной), если в процессе распространения волны вектор E совершает колебания вдоль определенного направления (в случае однородной среды – в одной плоскости).
Плоскостью поляризации линейно поляризованной волны будем называть плоскость колебаний ее электрического вектора E, (т.е. плоскость, проходящая через направление колебаний вектора E световой волны и направление распространения этой волны). Плоско поляризованную волну излучает, например, отдельный атом. Волна называется поляризованной по кругу (или волной с циркулярной поляризацией), если конец вектора E описывает в фиксированной плоскости, перпендикулярной направлению распространения волны, окружность. Если конец вектора E описывает в этой плоскости эллипс, то тогда говорят о эллиптически поляризованной волне.
Типы поляризованного света, метод описания поляризованного света подробно рассмотрено в лабораторной работе № 5.
Под поляризацией света понимают получение поляризованного света из естественного. Под естественным светом понимают свет, в котором направление колебаний вектора E в плоскости, перпендикулярной направлению распространения световой волны, изменяется случайным образом. Поляризованный свет получают следующими способами: 1) при прохождении света через кристаллы, в которых наблюдается двойное лучепреломление света; 2) при отражении света на границе раздела двух диэлектриков.
|
|
Прохождение света через поляризатор. Закон Малюса.
 |
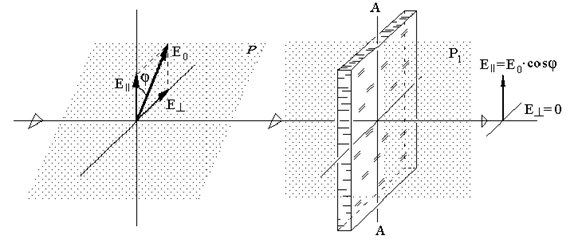Поляризатор представляет собой устройство для получения линейно поляризованного света. Поляризаторы можно использовать и для анализа поляризованного света, тогда их называют анализаторами. Действие поляризаторов основано на том, что они пропускают световые колебания лишь с определенной ориентацией вектора Е, которую называют осью поляризатора (плоскость колебаний вектора Е в этом случае называют плоскостью поляризатора).
Линейно поляризованная волна, падающая на поляризатор, может быть разложена на две взаимно перпендикулярные составляющие: Е|| – параллельную оси поляризатора, и Е ┴– перпендикулярную этой оси (см. рис.1).
Рис.1. Прохождение линейно поляризованного света через поляризатор.
Р – плоскость поляризации падающей плоскополяризованной волны,
P1 – плоскость поляризатора, АА – ось поляризатора.
Составляющая Е ┴, перпендикулярная плоскости Р1, поглотится поляризатором, а составляющая Е║ пройдет через поляризатор. Поэтому амплитуда волны, прошедшей через поляризатор, будет равна
E║ = E0·cosφ (1)
где E0 – световой вектор (напряженность электрического поля) падающей на поляризатор линейно поляризованный волны; φ – угол между направлением колебаний вектора напряженности электрического поля падающей на поляризатор линейно поляризованный волны и плоскостью поляризатора.
|
|
Интенсивность световой волны пропорциональна квадрату амплитуды напряженности, поэтому интенсивность света I1) прошедшего через поляризатор будет равна:
I = I0·cos2φ (2)
где I0 – интенсивность падающего на поляризатор линейно поляризованного света. Соотношение (3) носит название закона Малюса и формулируется следующим образом:
Интенсивность света, прошедшего через поляризатор пропорциональна интенсивности линейно поляризованного света, падающего на поляризатор и квадрату косинуса угла между плоскостью поляризации падающего света и плоскостью поляризатора.
При падении на поляризатор естественного света, интенсивность любых двух взаимно перпендикулярных составляющих всегда будут равны друг другу, поэтому интенсивность поляризованного света I, прошедшего через поляризатор, всегда будет равна I=I0/2, где I0 – интенсивность естественного света, падающего на поляризатор.
Если вращать поляризатор вокруг луча частично поляризованного света, то интенсивность света за поляризатором будет изменятся от Imax до Imin (переход от Imax к Imin совершается при повороте на угол, равный π/2). Величина
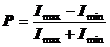∙100% (3)
называется степенью поляризации. Здесь Imax и Imin – соответственно максимальная и минимальная интенсивности частично поляризованного света, пропускаемого поляризатором. Для плоско поляризованного света: Imin = 0; P = 100%; для естественного света: Imax = Imin; P = 0%.
|
|
2.3. Отражение света на границе двух прозрачных сред. Формулы Френеля. Закон Брюстера.
Когда свет достигает границы двух прозрачных изотропных сред с разными оптическими свойствами, он частично проходит во вторую среду, изменяя направление в случае наклонного падения (преломляется), и частично возвращается в первую среду (отражается).
Направление отраженного и преломленного лучей света хорошо описывается законами геометрической оптики. Однако эти законы ничего не говорят о поляризации и интенсивности отраженного и преломленного света.
Введем термин коэффициент отражения (R) границы раздела двух сред, как отношение интенсивности света отраженного от поверхности к интенсивности падающего света:
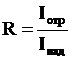(4)
Коэффициент отражения при наклонном падении луча зависит от поляризации падающего света. Поэтому разложим каждую из трех волн - падающую, отраженную и преломленную на две составляющие: поляризованную в плоскости падения, т.е. в плоскости, в которой лежит падающий луч и нормаль N, восстановленная из точки падения (снабдим эти составляющие индексом ||), и поляризованную в плоскости перпендикулярной плоскости падения (инд. ┴ ).
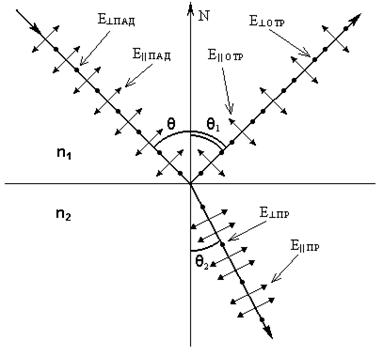
Рис.2. Направления векторов Е║и Е ┴ в падающей, отраженной и преломленной волнах.
Френелем из граничных условий для электромагнитного поля получены формулы для коэффициентов отражения составляющих световой
через угол падения θ и угол преломления θ2 луча.
, 
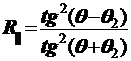(5)
Коэффициент отражения естественного света можно получить, если рассматривать его как сумму двух некогерентных волн одинаковой интенсивности
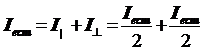(6)
Поэтому коэффициент отражения естественного света будет равен:
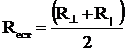. (7)
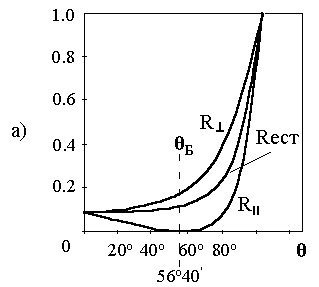
Из графиков на рис.3а видно, что при некотором угле падения R║= 0. Это следует и из формулы (7). При θ+θ2 = π/2 получим, что знаменатель равен бесконечности и выражение (5) для R║ обращается в нуль.Так как по закону преломления sinθ/sinθ2 = n2/n1, то при θ2 = π/2–θ получим:
 |
 |
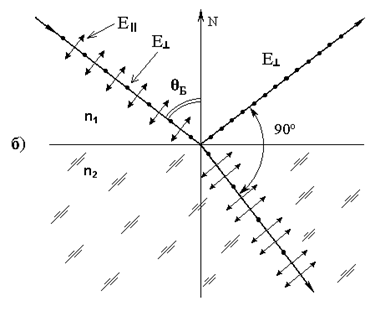Рис. 3. а) – Зависимость. коэффициентов отражения R от угла падения при переходе из воздуха (n1 = 1) в стекло (n2= 1, 5) и наоборот.
б) – Отражение и преломление света при падении его на границу раздела под углом Брюстера. волны параллельной R║ и перпендикулярной R┴ плоскости падения луча, выраженные
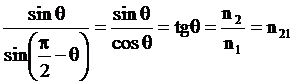, (8)
Здесь n21 представляет относительный показатель преломления второй среды относительно первой.
Следовательно, при падении света под углом θБр, определяемым выражением
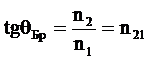(9)
составляющая, имеющая поляризацию параллельную плоскости падения, проходит во вторую среду полностью, не отражаясь (см. рис.3б), а составляющая, поляризованная перпендикулярно плоскости падения частично отражается.
Поэтому при падении на границу раздела естественного света под углом, определяемым выражением (9), отраженный свет будет линейно поляризован в плоскости, перпендикулярной плоскости падения, а преломленный - частично поляризованным.
Связь угла падения световой волны, при котором наблюдается линейная поляризация отраженной волны, с относительным показателем преломления света на границе двух сред (9) называется законом Брюстера, а соответствующий угол θБр – углом Брюстера.
2.4. Поляризация света при двойном лучепреломлении.
Фазовые пластинки.
 |
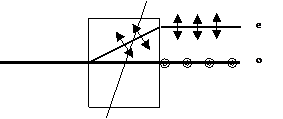О'
О
Рис.4. Распространение светового луча через анизотропный кристалл (например, исландский шпат) нормальном падении. ОО' – оптическая ось кристалла,
о – обыкновенный, е – необыкновенный лучи.
Двойное лучепреломление – это способность анизотропных веществ разделять падающий на них световой луч на два луча, распространяющихся в разных направлениях с различной фазовой скоростью и поляризованных во взаимно перпендикулярных направлениях (рис.4). Анизотропия веществ – это зависимость их физических свойств от направления.
Большинство кристаллов (кроме кристаллов кубической системы) анизотропны: их диэлектрическая проницаемость и показатель преломления зависят от направления колебаний светового вектора волны. Даже, когда первичный луч падает на кристалл нормально, преломленный луч разделяется на два: один из них является продолжением первичного, т.е. подчиняется обычному закону преломления света и его называют обыкновенным (о), а второй отклоняется, его называют необыкновенным (е).
Поляризаторы, поляризационные призмы, поляроиды – это устройства для получения и анализа поляризованного света, действие которых основано на явлении двойного лучепреломления.
В любом анизотропном кристалле всегда имеется одно или два направления, вдоль которого двойное лучепреломление отсутствует, и состояние его поляризации не меняется. Это направление называется оптической осью кристалла. В данном случае речь идет о направлении, а не о прямой линии. Любая прямая, проходящая параллельно данному направлению, является оптической осью кристалла. Существуют одноосные и двухосные кристаллы. В дальнейшем рассматриваются только одноосные кристаллы.
Плоскость, проходящую через направление луча света и оптическую ось кристалла, называют главной плоскостью одноосного кристалла. Колебания электрического вектора (вектора Е) в обыкновенном луче происходят перпендикулярно главной плоскости (следовательно, перпендикулярно оптической оси), в необыкновенном луче колебания происходят в главной плоскости (следовательно, вектор Е необыкновенного луча образует с оптической осью некоторые углы).
Из-за анизотропии кристалла показатель преломления в направлении оптической оси и в направлениях перпендикулярных ей имеет различные значения. Поэтому, скорость световых волн v = c/n зависит от направления колебаний электрического вектора. Колебания вектора Е при любом направлении обыкновенного луча перпендикулярны оптической оси кристалла, поэтому обыкновенный луч распространяется в кристалле по всем направлениям с одинаковой скоростью v0 = c/n0, где nо = const – показатель преломления кристалла для обыкновенного луча. Для необыкновенного луча угол между направлением колебаний вектора Е и оптической осью отличен от прямого и зависит от направления луча, а поэтому необыкновенный луч распространяется в кристалле по различным направлениям с разной скоростью (ve = c/ne, где nе ¹ const – показатель преломления кристалла для обыкновенного луча), зависящей от угла между вектором Е и оптической осью.
Предположим, что внутри одноосного кристалла точечный источник света S испускает световую волну. На рис.5 показано распространение обыкновенного и необыкновенного лучей в кристалле (главная плоскость совпадает с плоскостью чертежа, ОО' – направление оптической оси).
 |
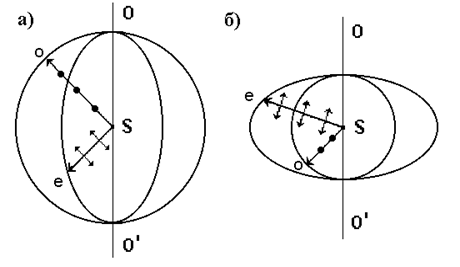Рис.5. Распространение обыкновенного (о) и необыкновенного (е) лучей в кристалле от точечного источника света S. ОО' – оптическая ось кристалла. Сплошными линиями изображены волновые поверхности обыкновенного и необыкновенного лучей. а) – положительный кристалл, б) – отрицательный кристалл.
Волновой поверхностью обыкновенного луча (vо = const) является сфера, волновой поверхностью необыкновенного луча (vе ¹ const) является эллипсоид. Если vо > vе (рис.5а), то такой одноосный кристалл называют положительным, если vо < vе (рис.5б), то такой одноосный кристалл называют отрицательным.
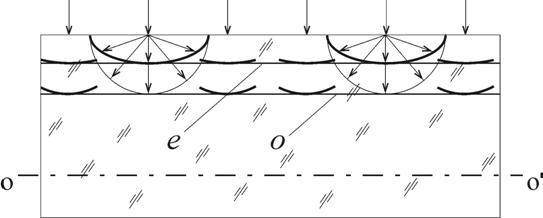
Рис.6. Распространение света через пластинку кристалла в направлении перпендикулярном оптической оси. ОО' – оптическая ось кристалла, е – волновая поверхность необыкновенного луча,
о – волновая поверхность обыкновенного луча.
Пусть свет падает нормально на поверхность положительного кристалла, оптическая ось которого параллельна преломляющей поверхности (рис.6). Обыкновенные и необыкновенные лучи в этом случае распространяются вдоль одного и того же направления, но с разной фазовой скоростью (vо > vе); при выходе из кристалла лучи приобретают разность фаз. Так как эти лучи плоско поляризованы во взаимно перпендикулярных плоскостях, то это дает возможность изменить тип поляризации.
Пусть на пластинку кристалла падает линейно поляризованная волна, вектор E которой образует некоторый угол α с оптической осью кристалла (см. рис.7).
На границе двух сред падающая волна разделяется на две составляющие Ео и Ее, которые в толще кристалла будут распростра няться с различной скоростью, в результате чего на выходе из пластинки между этими составляющими возникнет оптическая разность хода:
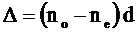(10)
и, соответственно, разность фаз:
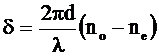(11)
Рис.7. Прохождение линейно поляризованного света через пластинку анизотропного кристалла толщиной d. ОО' – оптическая ось кристалла.
 |
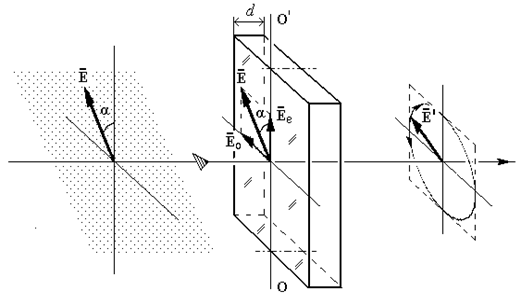Кристаллическая пластинка, которая вносит дополнительную разность фаз между двумя взаимно перпендикулярными составляющими падающей на нее световой волны, называется фазовой пластинкой. Поэтому, прошедшая пластинку волна, станет в общем случае эллиптически поляризованной.
Чтобы с помощью фазовой пластинки можно было получить из линейно поляризованного света свет с круговой поляризацией, а из круговой, наоборот, – линейно поляризованный, необходимо, чтобы угол между осью кристалла и направлением вектора E был равен π/4, а разность фаз между взаимно перпендикулярными составляющими при прохождении пластинки равнялась
, (12)
где m – целое число. Оптическая разность хода при этом будет равна
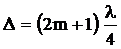(13)
Из формулы (11) видно, что при заданных nо и nе это условие удовлетворяется подбором толщины пластинки d. В результате при
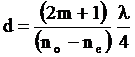(14)
получается, так называемая, пластинка в четверть длины волны (пластинка λ/4).
В оптике используется пластинка и в половину длины волны (пластинка λ/2). На выходе такой пластинки колебания Ео и Еe сдвинуты по фазе на p. Свет, выходящий из такой пластинки, остается линейно поляризованным. Однако, его плоскость колебаний результирующего вектора E будет повернута симметрично относительно главной плоскости пластинки.
Четвертьволновая и полуволновая пластинки используются для анализа состояния поляризации световой волны.
Явление двойного лучепреломления лежит в основе работы устройств, служащих для получения поляризованного света – поляризаторов (призм) и поляроидов. Поляризаторы делятся на два класса:
1) поляризаторы, дающие только линейно поляризованный луч (или поляризационные призмы). Они состоят из двух склеенных призм и обыкновенный луч отводится в сторону из-за полного отражения от границы раздела призм. Примером может служить призма Николя.
2) поляризаторы, дающие два поляризованных во взаимно перпендикулярных плоскостях луча (или двоякопреломляющие поляризационные призмы). В этих призмах используют различие в показателях преломлениях обыкновенного и необыкновенного лучей, чтобы развести их возможно дальше друг от друга.
Поляроиды – это приспособления представляющие собой тонкую пленку из прозрачного материала, в которую вкраплены двоякопреломляющие кристаллики, обладающие свойством дихроизма. Дихроизм – это различное поглощение света в кристаллах в зависимости от ориентации вектора Е световой волны. Примером дихроичного кристалла является герапатит (сернокислый иод-хинин). Установлено, что такие пленки уже при толщине 0,1 мм полностью поглощают обыкновенные лучи видимой области спектра и выходят только необыкновенные лучи. Преимущество поляроидов перед призмами – это возможность изготавливать их с площадями поверхностей до нескольких квадратных метров.
Порядок выполнения работы
3.1. Анализ поляризации лазерного излучения.
 |
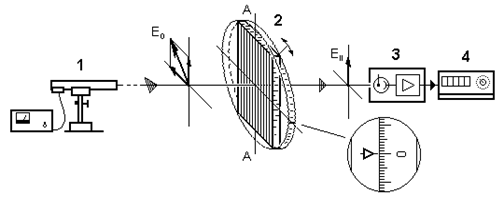Рис.8.Схема установки для анализа поляризации света, где
1–лазер, 2–поляризатор, 3–фотоприемник, 4–вольтметр, АА–ось поляризатора.
3.1.1. Включите питание лазера, вольтметра и гониометра тумблерами "Сеть".
3.1.2. Проверьте ход лазерного луча. Луч лазера (самый яркий) должен попадать во входное отверстие фотоприемника 3. Присутствующие слева и справа менее яркие лучи являются переотражениями луча лазера от стеклянных поверхностей поляризатора и фотоприемника.
3.1.3. Вращая поляризатор 2, укрепленный на держателе со шкалой, снимите зависимость интенсивности, проходящего через него света, от угла поворота поляризатора. Измерения проведите по всей окружности с шагом 15°. Интенсивность света в относительных единицах измеряется вольтметром. Результаты измерений занесите в таблицу 1.
Таблица 1
| φ,град | ||||||||||||
| I, отн.ед. | ||||||||||||
| cos2φ | ||||||||||||
| I / Imax | ||||||||||||
| φ, град | ||||||||||||
| I,отн.ед. | ||||||||||||
| cos2φ | ||||||||||||
| I / Imax |
3.1.4. Вблизи максимумов и минимумов интенсивности, записанных в таблице 1, медленным вращением поляризатора найдите более точное положение двух максимумов и минимумов и занесите их в табл. 2.
Таблица 2
| φ,град | Imax,отн.ед. | φ,град | Imin,отн.ед. | P,% |
Все вычисления выполняются компьютером, а именно:
3.1.5. Строится в полярных координатах зависимость интенсивности света (нормированной на ее максимальное значение), прошедшего через поляризатор, от угла поворота поляризатора I/I max = f (φ). Значение Imax берутся из таблицы 2, а значения I - из таблицы 1.
3.1.6. На том же графике строится теоретическая зависимость, отражающая закон Малюса I/I0 = cos2 φ.
3.1.7. Рассчитывается, используя формулу (3), степень поляризации лазерного излучения (P)..
Результаты расчетов отображаются в таблице и построенном графике.
3.1.8. Проанализировав таблицу и графики и значение степени поляризации сделайте вывод о состоянии поляризации лазерного излучения. Определите ориентацию вектора напряженности электрического поля лазерного излучения в пространстве.
Примечание: Принцип получения линейно поляризованного излучения в гелий-неоновом лазере рассмотрен в Приложении 2.