Теорема (существующее и единственное решение задачи Коши)

III Дифференциальные уравнения

32. ДУ 1 порядка: вид, задачи Коши, геометрический смысл.

Имеет вид

Если уравнение можно разрешить относительно , то его можно разрешить

- ДУ 1 порядка разрешенное относительно порядка

Уравнение устанавливает связь между координатами точка (x;y) и угловым коэффициентам к касательной к интегральной кривой, проходящей через эту точку отсюда следует дифференциальное уравнение дает совокупность направлений на плоскости x и y – геометрический смысл ДУ 1 порядка

Опр. Кривая во всех точках в которой направлена одинаково называется изоклиной, уравнения изоклины можно получить если положить то есть , условие что при функция y должна быть равна заданному числу то есть (называется начальным условием.

Начальное условие записывается в виде:

Общим решением ДУ 1 порядка называется функция содержащая одну постоянную и удовлетворяющую условию одной

1. функции является решением ДУ при каждом фиксированном С.

2) Какого бы ни было начальное условие , можно найти такое значение постоянной равной c=c₀, что функция 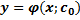удовлетворяющих данному начальному условию.

Теорема (существующее и единственное решение задачи Коши)

Если в уравнении .. 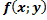и ее частная производная 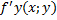непрерывный вектор области Д содержащей точку (x₀;y₀) то сумма единственного решения этого уравнения удовлетворяет начальному условию при .

Геометрический смысл теоремы – состоит в том, что при выполнении ее условия существует единственная интегральная кривая ДУ, проходит через точку (x₀;y₀)

33. ДУ 1 порядка с разделяющимися переменными

Опр. Уравнения вида 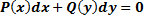называется ДУ 1 п орядка с разделяющимися переменными. Оно решается непосредственным интегрированием p(x)+q(y)=c – общий интеграл, где p(x) и q(y) – первообразная для функции P и Q

Опр 2. Уравнения вида называется ДУ 1 порядка с разделяющимися переменными, с учетом что или или 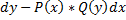делим на проинтегрировав получим интеграл.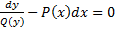

Опр 3. Уравнение вида: называется ДУ с разделяющимися переменными. Для нахождения данного ДУ, обе части данного уравнения необходимо разделить на выражение получим . Проинтегрировав последнее равенство, получим общий интеграл.

34. Линейные ДУ 1 порядка

ДУ 1 порядка называется линейным, если его можно записать в виде: , где Р(х) и Q(x) – заданные функции.

Если Q(x)=0 то уравнения называется линейным однородным ДУ 1 порядка

Если Q(x)≠0 то уравнения 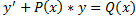называется линейным неоднородным ДУ 1 порядка

35. Однородные ДУ 1 порядка

Опр1. Уравнение y ‘=f(x,y) называется однородным, если его можно представить как функцию аргумента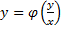

Опр2. Уравнение P(x;y)dx+Q(x;y)dy=0, называется однородным если P(x;y) и Q(x;y) однородные функции одного измерения (т.е. в них свободный член равен 0, а каждое слагаемое имеет одинаковую степень.

Уравнения данного типа решается с помощью введения новой переменной. подстановка

Подставив y и y’ в уравнения или P(x;y)dx+Q(x;y)dy=0 получим ДУ с разделяющими переменными

36. ДУ 2 порядка: вид, задачи Коши, геометрический смысл

ДУ 2 порядка в общем случае имеет вид . Общем решением данного уравнения называется функция Где - незявисящие от х постоянные удовлетворяющие условиям:

• функция от является решением ДУ для каждого значения

• какого бы не было начальное условие y(x=x₀)=y₀ y’(x=x₀)=y’₀ существуют единственные значения постоянной и является таким что функция является решением уравнения и удовлетворяющих начальным условиям y (x=x₀)=y₀ y’(x=x₀)=y’_0, всякое решение уравнения полученного из общего при конкретных значениях постоянных 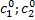и равно постоянным и называется частным решением.

График ДУ 2 порядка называется интегральной кривой. Общее решение ДУ представляет собой множества кривых, частное решение кривых, одна кривая части этого множества проходят через точку (x₀;y₀) и имеющая в ней касательную с заданными условиями коэффициентами. y’(x₀)=y’

Задача нахождения решения ДУ, удовлетворяющего заданным начальным условием называется задачей Коши.

37. Ду 2 порядка, решающиеся методом понижения порядка

– решение данного ДУ находим в двукратном интегрировании

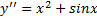
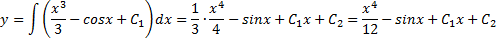
Замечание ДУ n порядка вида. решается аналогично n кратным интегрированием.

38. Линейные однородные ДУ 2 порядка. Теоремы о частных решениях

39. Фундаментальная система частных решений линейного однородного ДУ 2 порядка

40. Определитель Вороновского и его свойства

41. Основная теорема

42. Линейные неоднородные ДУ 2 порядка. Теоремы о частных решениях.

Линейным ДУ называется такое ДУ, в котором неизвестная функция и все её производные входят в первых степенях не перемножаясь между собой.

В зависимости ль вида правой части уравнения y”+p*y ’+q*y=f(x) и корней соответственно характеристического уравнения возможны случаи:

1)

P(n)- многочлен степени n

А) Если α является корнем характеристического уравнения

- многочлен степени n с неопределенным коэффициентом

Б) если α является корнем характеристического уравнения то:

t- кратность корня α

2) P(x)=P_n(x)

а) если 0 не является корнем характеристического уравнения то:

б)) если 0 является корнем характеристического уравнения то:

3)

А) еслине являются корнемхарактеристического уравнения то

Б) если являются корнемхарактеристического уравнения то

4)