6.1. Термический КПД тепловой машины:
где А – работа, совершаемая рабочим телом (газом) за цикл; Q 1 – количество теплоты, полученное рабочим телом за цикл от нагревателя; Q 2 – количество теплоты, отданное за цикл окружающим телам.
6.2. Термический КПД цикла Карно – наиболее экономичного обратимого кругового процесса, состоящего из двух изотерм и двух адиабат (рис. 3):
где Q1 – количество теплоты, которое газ получает при изотермическом расширении 1-2 при температуре нагревателя Т 1; Q2 – количество теплоты, отданное газом при изотермическом сжатии 3-4 при температуре холодильника Т 2. Рис.3
Пример 7. Температура пара, поступающего в паровую машину,
t 1 = 1270C; температура в конденсаторе t 2 = 270C. Определить теоретически максимальную работу при затрате количества теплоты Q = 4,2 кДж.
Дано: t 1 = 1270C; T 1 = 127+273 = 400K; t 2 = 270C; T2 =300K; Q1=Q =4,2 кДж.
Найти: А.
Решение. Для того чтобы работа, совершаемая тепловым двигателем, была максимальной, необходимо, чтобы цикл, по которому работает двигатель, был обратимым. При наличии только двух термостатов – нагревателя (Т 1) и холодильника (Т 2) – возможен только один обратный цикл – цикл Карно, состоящий из двух изотерм и двух адиабат (рис.3).
Коэффициент полезного действия этого цикла:
, (1)
но КПД любого теплового двигателя:
, (2)
где А – полезная работа, совершаемая двигателем за цикл; Q 1 – количество теплоты, полученное рабочим телом от нагревателя (в цикле Карно – это теплота, полученная в процессе изотермического расширения газа 1-2).
Приравнивая выражения (1) и (2), находим работу А:
Откуда
кДж.
Ответ: А = 1,05 кДж.
ЯВЛЕНИЯ ПЕРЕНОСА
7. 1. Средняя длина свободного пробега молекулы газа:
|
|
где d эф – эффективный диаметр молекул газа; n – концентрация молекул газа.
7.2. Закон Фика для диффузии:
,
где Δ М – масса вещества, перенесенная в результате диффузии через площадь S, перпендикулярную оси X, за время Δt;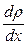 
- градиент плотности данного вещества; D - коэффициент диффузии этого вещества.
7.3. Коэффициент диффузии для газов:
где 
- средняя скорость теплового движения газовых молекул; 
- средняя длина свободного пробега молекул.
7.4. Импульс (количество движения), передаваемый молекулами от слоя к слою через элемент поверхности площади S за время Δt:
где 
- градиент скорости течения слоев; 
– динамическая вязкость (коэффициент внутреннего трения).
7.5. Динамическая вязкость газа:
где ρ – плотность газа.
7.6. Закон Ньютона для силы внутреннего трения:
где F –сила внутреннего трения между движущимися слоями газа или жидкости, рис. 4. Рис.4
7.7. Закон Фурье для теплопроводности:
где ∆Q – количество теплоты, переносимой посредством теплопроводности через площадь S, перпендикулярную оси X, за время Δt; λ - коэффициент теплопроводности; 
- градиент температуры.
7.8. Коэффициент теплопроводности газа:
,
где 
– удельная теплоемкость газа при постоянном объеме.
Пример 8. На высоте h = 20 см над горизонтальной трансмиссионной лентой, движущейся со скоростью u 1 = 70 м/с, подвешена параллельно ей пластинка площадью S = 4 см2 (рис.5). Какую силу надо приложить к этой пластинке, чтобы она оставалась неподвижной? Вязкость воздуха при нормальных условиях 
Па×с. В условиях опыта температура t =270С.
Дано: h= 20 см, и1 = 70 м/с, S = 4 см2, 
Па×с, t= 27 0C, Т = 300 К.
|
|
Найти: F.
Решение. Cлои воздуха, непосредственно находящиеся над движущейся лентой, увлекаются ею, и в воздухе создается некоторый градиент скоростей . Между слоями движущегося воздуха создается сила трения F mp. Эта сила действует и на пластинку со стороны движущихся слоев. Пластинка будет неподвижна, если приложенная внешняя сила F и сила трения Fmp скомпенсируются, т. е. Рис.5
Сила трения может быть найдена по уравнению Ньютона:
, (1)
где 
- производная скорости и движения слоя по координате z, причем ось oz перпендикулярна плоскостям трансмиссии и пластинки, направлена от трансмиссии к пластинке.
Вязкость газа η может быть рассчитана по формуле:
Как видно, вязкость зависит только от природы газа (эффективного диаметра молекул d и молярной массы μ) и температуры T. Сравним вязкость при температуре Т с вязкостью при нормальных условиях (Т0 = 273К):
.
Вязкость η при температуре Т связана с вязкостью η0 при нормальных условиях соотношением:
. (2)
Градиент скорости направленного движения слоев газа считают постоянным. Производная 
, ее можно заменить отношением изменения скорости Δи к приращению координаты Δz, Δи = (0 – и1), Δz = h (рис.5):
. (3)
Подставляя выражения (2) и (3) в уравнение (1), получим:
.
Проверим размерность:
Н
Произведем вычисления:
Н.
Ответ: F = 2,5∙10-6 H.
РЕАЛЬНЫЕ ГАЗЫ
8.1. Уравнение Ван-дер-Ваальса для реального газа:
· для одного моля газа 
· для произвольной массы газа m
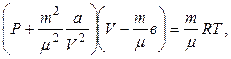
где Р – давление газа на стенки сосуда; а, в – постоянные Ван-дер-Ваальса, рассчитанные для одного моля газа (см. Приложение); V μ – объем, занимаемый одним молем газа; V – объем, занимаемый газом.
|
|
8.2. Внутреннее давление в газе, обусловленное силами взаимодействия молекул:
или 
Пример 9. 2 моля азота охлаждены до температуры –1000С. Определить давление Р, оказываемое газом на стенки сосуда, если объем, занимаемый газом, равен 0,1 л. Сравнить полученное давление Р с давлением Р ид, которое имел бы азот, если бы сохранил при рассматриваемых условиях свойства идеального газа.
Дано: 
= 2 моля; t = - 100 0C; Т = 173 К; V = 0,1л = 0,1ּ10-3 м3 = 10-4 м3.
Найти: Р/Рид.
Решение. Из уравнения состояния реального газа выразим давление Р:
Значения постоянных а и в находим по Приложению:
для азота а = 0,135 Н∙м 4/моль 2; в = 3,9 10-5 м3/моль.
Произведем вычисления:
Па.
Для сравнения найдем давление Рид из уравнения состояния идеального газа 
:
Рид = 2 8,31∙173/10-4 = 2880 ∙104 = 0,28 ∙108Па = 280 105Па.
Тогда 
.
Следовательно, в этом случае уравнение Менделеева-Клапейрона непригодно для описания состояния охлажденного и сжатого азота.
Ответ: 
.