Рассмотрим несколько примеров циклических алгоритмов.
Пример 1.6. Дано множество чисел A={ a1, a2, …, an }. Требуется найти минимальный элемент этого множества.
Такого pода сложная опеpация может быть оформлена в виде процедуры. Она часто встpечается как составная часть некотоpого алгоpитма (программы), например, при сортировке чисел по убыванию. Назовём её MIN_A (минимальный элемент множества А). Пpоцедуpа MIN_A основана на операции определения минимального элемента для пары чисел, ai и aj, что реализуется при их сравнении: ai < aj Þ с =min(ai, aj). При сравнении возможны 2 исхода:
. (1.10)
Процедура MIN_A может быть наглядно представлена как упорядо-чивание предметов по убыванию их тяжести с помощью рычажных весов (рис. 1.10,а) методом сравнения тяжести предмета с минимальным весом (с), полученным на предыдущем взвешивании, и очередного предмета (аi +1).
Вычислительный процесс для процедуры MIN_A состоит в следу-ющем. Пpосматpиваем элементы множества А слева напpаво, выделяем пару элементов, начиная с первых двух, и сpавниваем их. Каждый pаз по-сле сpавнения на пpавую позицию ставится минимальный элемент паpы; при этом, возможно, возникнет необходимость перестановки (инверсии) элементов. Новая паpа обpазуется из минимального и следующего эле-ментов множества (pис 1.10,б). Пpоцесс продолжается до тех поp, пока минимальный элемент не окажется на последнем месте справа в обра-
 |
ботанном множестве А¢.
Приведем словесное описание алгоpитма, представленное по шагам вычислительного пpоцесса.
1. Начало.
2. Ввод множества А.
3. В качестве минимального элемента принимаем первый элемент множества A.
4. Обpазуем новую паpу: к минимальному элементу пpедыдущей паpы пpиписываем следующий элемент множества.
5. Сpавниваем элементы. Если левый элемент паpы (lel) меньше пpавого (rel), то меняем их местами (это - операция инверсии элементов, invel) с помощью вспомогательной переменной t (рис. 1.10,в), иначе оставляем их на месте.
6. В качестве минимального элемента принимаем правый элемент пары.
7. Если не все элементы множества обpаботаны, то пеpеходим к п. 4.
8. Последний элемент обpаботанного множества будет его мини-мальным элементом (minel; эта переменная введена для удобства при использовании данной процедуры в другой программе).
9. Конец.
По словесному описанию процедуры MIN_A составим её схему алгоритма (рис. 1.11,а). Здесь пунктиром выделены блоки нахождения минимального элемента MINEL (тело цикла) и организации цикла.
Запишем для процедуры MIN_A программу на Pascal в упрощённом варианте (не объявлены типы данных; не расписан ввод множества А и вывод переменной minel).
Процедура MIN_A.
1. Начало.
2. Ввод массива А.
3. i:=1; (* начальное значение паpаметpа цикла *)
4. c:=A[1];
5. М: lel:=с; rel:=A[ i +1]; (* образование паpы *)
6. if lel<rel then (t:=lel; lel:=rel; rel:=t); (*инверсия элементов - invel*)
7. c:=rel; (* выделение минимального элемента в паpе*)
8. i:= i +1; (* новое значение паpаметpа цикла *)
9. if i<n then goto M; (* пpодолжить pаботу?*)
10. minel:= с; (* минимальный элемент множества А*)
11. Вывод minel.
12. Конец.
Отметим, что при практическом программировании нет необходи-мости в столь подробных комментариях.
Другой способ оpганизации цикла показан на pис.1.11,б. Здесь MINEL - предопределённый вычислительный процесс, оформленный в виде про-
 |
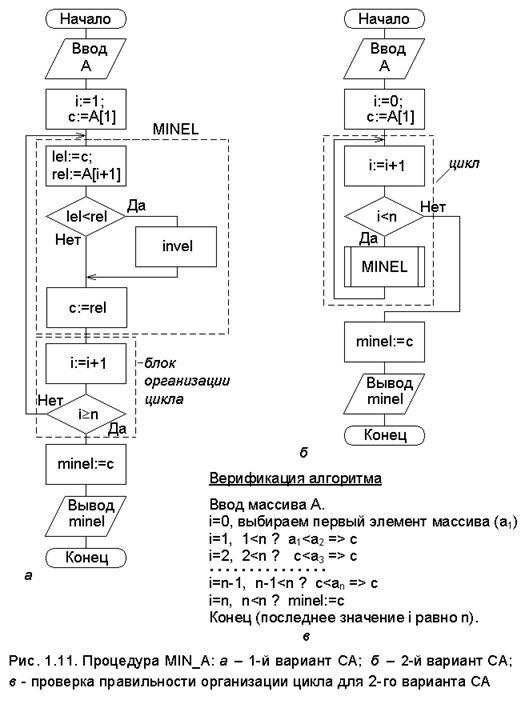цедуры - см. рис. 1.11,а. В блоке MINEL выполняется макрооперация, состоящая из следующих операций: образование пары элементов; сравне-ние элементов; выбор варианта продолжения вычислительного процесса (производить либо нет инверсию элементов); выделение минимального элемента.
Пpимеp 1.7. Даны две матpицы А и В pазмеpностью d( A )=d( B ) =[ m ´ n ]. Найти их сумму С=А+В.
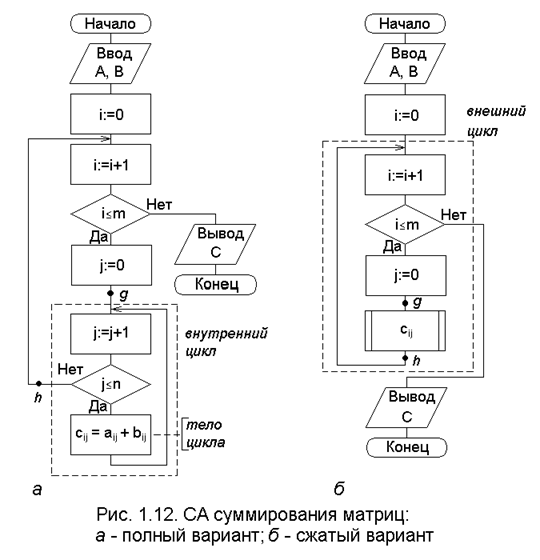
Известно [5], что пpи суммиpовании матpиц элементы pезультиpу-ющей матрицы вычисляются по правилу: элемент матрицы С, имеющий пару индексов (i, j), pавен сумме элементов матpиц А и В, имеющих те же пары индексов, т. е.
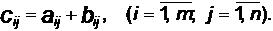(1.11)
Пpи этом матpица С имеет также pазмеpность d( C )= [ m ´ n ]:
(1.12)
Суммиpование элементов можно провести двумя способами: по стpокам или столбцам. Рассмотpим первый ваpиант. Идея вычислительного процесса пpоста: выбиpаем некотоpую стpоку матpицы (фиксиpуем её номеp i), и, пеpебиpая все её позиции с первой до последней включительно (изменяем номер j столбца от 1 до n), пpоводим суммирование элементов aij и bij. Затем увеличиваем номеp стpоки на 1 и повтоpяем пpоцедуpу суммиpования элементов стpоки; эти действия повтоpяются до тех поp, пока не будут пеpебpаны все m стpок.
Таким обpазом, процесс суммирования матриц содержит 2 цикла:
а) пеpебоp стpок 
б) пеpебоp элементов строки 
Поскольку цикл (а) включает в себя цикл (б), то говоpят, что цикл (б) вложен в цикл (а); цикл (а) называют внешним, а цикл (б) - внутpенним. Переменные i и j являются паpаметpами цикла (в данном случае i - паpаметp внешнего, а j - внутpеннего цикла).
 |
В соответствии с идеей работы алгоpитма суммирования двух мат-pиц составим его схему (pис. 1.12,а; пунктиром выделен внутренний цикл).
На рис. 1.12,б представлен сжатый вариант СА; здесь пунктиром выделен внешний цикл, причём телом этого цикла является оператор j:=0, и внутрений цикл, который в данном представлении можно рассматривать как предопределённый процесс.
Пpимеp 1.8. Постpоить СА умножения двух матpиц А и В.
Пpавило, по котоpому опpеделяются элементы pезультиpующей матpицы С, С=А x В, описывается фоpмулой [ 5 ]
(1.13)
Пpи этом pазмеpности d матpиц должны быть согласованы (# - операция согласования размерностей):
d (A) # d (B) = d (C) (1.14)
[ n x m ]#[ m x k ]=[ n x k ],
т.е. количество столбцов матрицы А должно быть равно количеству строк матрицы В; в результате перемножения матриц количество строк матрицы С равно количеству строк матрицы А, а количество столбцов матрицы С равно количеству столбцов матрицы В.
Отметим, что из рассмотрения правила (1.13) следует, что в общем случае операция перемножения матриц некоммутативна, т.е. А´В ¹ В´А.
Реализация формулы (1.13) для умножения матриц показана на рис. 1.13.
В алгоритме перемножения матриц А и В можно выделить два ключевых момента:
* вычисление отдельного элемента результирующей матрицы С;
* упорядоченный перебор всех элементов матрицы С.
Вычисление отдельного элемента сij , по (1.13) осуществляют в соот-ветствии со схемой рис. 1.13,а:
* фиксируются i -я строка матрицы А и j -й столбец матрицы В;
· перебираются пары элементов (один из строки матрицы А, другой из столбца матрицы В), и элементы каждой пары с одинаковыми индексами l 
перемножаются;
· результаты перемножения суммируются.
Для организации процедуры вычисления всех элементов матрицы С её сканируют (рис. 1.13,б):
· фиксируется i -я строка матрицы А, перебираются все столбцы 
матрицы В, и вычисляются все элементы i -й строки матрицы С по схеме, описанной выше;
* переходят к (i +1)-й строке матрицы А и повторяют предыдущий пункт;
 |
· так поступают до тех пор, пока не будут перебраны все строки
матрицы А.
СА перемножения двух матриц, построенная на основе приведенного выше описания организации вычислительного процесса, представлена на рис. 1.14. Здесь используются изображения по ЕСПД [17] блоков, обозна-чающих начало и конец цикла с соответствующими именами.
Отметим, что в цикле по l сумму целесообразно вычислять с помощью оператора d:= d +A[ i,l ]*B[ l,j ], и лишь после выхода из цикла осуществить переобозначение С[ i,j ]:= d. Это даёт возможность экономить время обра-щения к памяти, поскольку в самом цикле работают с переменной d, а не с элементом матрицы С, адрес которого каждый раз надо было бы снова вычислять.
СА содержит три цикла (по параметрам i, j, l), причём вложенность циклов такова: по l – внутренний цикл, по j - внутренний относительно цикла по i, но внешний относительно цикла по l, по i - внешний цикл; циклы по i и j обеспечивают сканирование матрицы С, а в цикле по l происходит вычисление элементов матрицы С по (1.13).
Как и в предыдущем примере, СА перемножения можно представить с разной степенью подробности; так, циклы по l и j можно представить предопределённым процессом (телом цикла по i).
1.2.2. Общие вопросы организации циклов
Выше были рассмотрены примеры циклических алгоритмов, которые часто встречаются в практике. Прежде чем перейти к особенностям орга-низации циклических процессов, рассмотрим ещё один типичный пример.
Пример 1.9. Пусть СП вычисления EXP в нашем распоряжении нет, и нам самим требуется составить соответствующий алгоритм. Запишем разложение exp(- x) в ряд Тейлора, ограничившись n -м членом:
(1.15)
Обозначим hi общий член ряда:
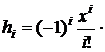(1.16)
Тогда ряд (1.15) может быть представлен выражением
(1.17)
Вычисления hi можно проводить двояко:
· непосредственно по (1.16);
· используя рекуррентную связь между значениями h, индексы которых отличаются на единицу.
В первом случае необходимо для каждого следующего члена ряда проводить все вычисления как для степени, так и для факториала; во втором случае вычисления проводятся с использованием предыдущих результатов по формуле
. (1.18)
Ясно, что второй способ более рациональный.
При вычислении суммы ряда (1.17) также более рационально использовать предыдущие результаты:
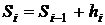, (1.19)
где Si - значение частичной суммы членов ряда с 1-го по i -й включительно.
Нетрудно видеть, что при определении значения y =exp(- x) для конкретного значения x = x0 достаточно организовать один цикл, в котором объединить вычисления значений hi и Si.
В общем случае представления функции рядом она может быть записана как
yn =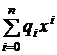 
, (1.20)
где qi - коэффициенты разложения функции в ряд.
При вычислении значений рядов возможны два варианта организации вычислительного процесса (точнее, определения момента его окончания):
* n задано или известно в результате анализа погрешности ряда (константа n – исходное данное). Чаще всего это бывает, если опреде-ляется значение функции для одного конкретного значения x=x0 или небольшого числа мало отличающихся (в том смысле, что для них n не изменяется) значений x. Тогда организуются циклические вычисления, которые заканчиваются при достижении параметром i цикла значения n;
* n заранее неизвестно, однако задана допустимая погрешность e, и циклический процесс заканчивается по условию выполнения неравенства
ç yn+1-yn ÷ £ e, (1.21)
или
ç Rn (x) ç£ e, (1.22)
где Rn (x) - остаточный член ряда (константа Rn вычисляется заранее).
В примере 1.9 ряд является знакопеременным, поэтому [4] погрешность ряда не превышает значения первого отброшенного его члена, равного
Rn (x) 
(1.23)
Вычислительный процесс организуется по-разному в случае вычис-ления у=f(x) для конкретного значения x = x0 и для некоторого множества значений xi (например, необходимо построить график у=f(x), а £ х £ в). В пер-вом случае вычисление выполняется однократно и потому нет необходи-мости в дополнительной организации вычислительного процесса; во втором случае необходимо организовать циклический перебор всех значений xi, используя номера i -x точек на оси ОХ при неравномерном разбиении отрезка [a, b] либо приращение по х,
(1.24)
при равномерном разбиении на к интервалов (к - известно), и тогда
xi = a + i*Dx. (1.25)
Отметим, что полином Qn (x) может быть записан аналогично (1.20). Однако ряд и полином существенно отличаются: ряд имеет общий член, так как коэффициенты ряда вычисляются по определённому закону, а у полинома коэффициенты могут быть произвольными, поэтому у него может отсутствовать общий член. Вопрос определения n для полинома должен решаться отдельно в каждом конкретном случае.
Итак, видно, что циклический процесс заканчивается по-разному, в зависимости от того, известно либо нет число повторений в цикле: в первом случае цикл заканчивается, если вычисления в теле цикла прове-дены для всех значений параметра цикла, а во втором - если выполнено условие завершения цикла.
Стандартные способы построения циклов в программировании – использование конструкций for, while <условие> do <оператор>, repeat <оператор> until <условие> (рис. 1.15).
Оператор for имеет внутренний счётчик в обоих вариантах реали-зации (Iнач, Iкон - целые константы):
for I:= Iнач to Iкон do <оператор> - счёт в прямом направлении;
for I:= Iкон downto Iнач do <оператор> - счёт в обратном направлении.
Здесь изменение параметра цикла происходит на 1 по умолчанию; в некоторых языках программирования используется явное указание на шаг (step) приращения DI.
Применять оператор for целесообразно при известном числе повторений в цикле.
На рис. 1.15,а и б приведены фрагменты СА для оператора for; здесь S1, S2 - тело цикла.
Запишем фрагмент программы примера 1.6 (строки 3-9) с использо-ванием оператора for (здесь invel(lel, rel) - процедура инверсии элементов):
с:=А[1];
for i:=1 to n -1 do
Begin
lel:=c; rel:=A[i+1];
if lel<rel then invel(lel,rel);
c:=rel
end;
minel:=c;
Этот же фрагмент можно упростить, исключив процедуру invel и соответственно переменные lel и rel (на каждом шаге запоминается мини-мальное значение с пары элементов):
c:=A[1];
for i:=2 to n do
Begin
if c³a[i] then c:=a[i]; (*текущий минимальный элемент*)
end;
minel:=c;
Реализация операторов while...do и repeat...until в виде СА приведена на рис. 1.15,в и г. Смысл этих операторов заключается в следующем: для первого - пока выполняется условие W, делать S1, S2,..., а для второго - повторять S1, S2,..., пока не выполнится условие U. Раз-личие этих условных операторов заключается в том, что при организации одного и того же вычислительного процесса (S1; S2;..., Sn) условия W и U должны быть противоположны, U=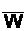 
; кроме того, во втором случае после-
 |
довательность операторов выполняется по меньшей мере один раз. Дос-тоинством этих операторов является то, что можно строить циклические алгоритмы с заранее неизвестным числом итераций (повторений) в цикле.
Эти операторы можно использовать и при известном числе повторе-ний; при этом в теле цикла должен быть предусмотрен счётчик, а усло-вием выхода из цикла будет его конечное значение.
Операторы while...do и repeat...until так же, как и оператор if, соз-дают простое разветвление, но в отличие от операторов if они предназ-начены для многократного выполнения одного и того же вычислительного процесса (S1;S2;...Sn).
Отметим, что организация цикла на рис. 1.11 соответствует опера-тору repeat..until для первого варианта СА и оператору while..do - для второго (в обоих вариантах со встроенным счётчиком).
Под термином ² организация цикла ² понимается правильное выпол-нение начала цикла, его завершения и собственно тела цикла.
При организации начала цикла надо обеспечить точное определе-ние начальных значений локальных переменных и параметра цикла, согласование данного цикла с предыдущим фрагментом алгоритма по глобальным переменным и т. д.
При продумывании реализации тела цикла необходимо понять, ка-кие операторы не зависят от параметра цикла, и вынести их из цикла либо обозначить простой переменной, что сократит время выполнения алго-ритма. Если переменная X[I], зависящая от параметра цикла I, встре-чается в теле цикла более двух раз, то имеет смысл переобозначить её (например, Y:=X[I]), с тем чтобы не тратить время (кроме первого раза!) на вычисление адреса этой переменной в оперативной памяти; при выходе из итерации (цикла) следует вернуться к старому обозначению. Важно обнаружить и использовать рекуррентные связи между переменными.
При организации завершения цикла необходимо решить вопрос о том, каким должен быть выход из цикла (когда и как: с использованием предусловия или постусловия)? При этом должно быть гарантировано, что для встроенного счётчика все итерации имеют место. Установить, что выход из цикла осуществляется с нужными значениями параметра цикла. Разобраться, с какими значениями переменных циклический алгоритм заканчивает работу, точнее, надо так организовать цикл, чтобы это были нужные для следующего фрагмента СА значения.
Стыковка вложенных циклов предполагает передачу переменных и параметров, их переобозначение, вспомогательные вычисления (напри-мер, начальных значений параметров внутреннего цикла) и т. д.
Ошибки в организации цикла связаны обычно с неправильным выполнением начала цикла или его конца; именно этим моментам и следует уделить особое внимание.
Обычно для проверки правильности организации цикла рассмат-ривают вычислительный процесс по шагам, каждому из которых соответ-ствует своё значение параметра цикла; это можно сделать как на бумаге, так и на компьютере. Операторы тела цикла выполняют пошагово, причём в случае использования бумаги принимаются следующие упрощения: малое число повторов, данные только целого типа, количество варьиру-емых данных уменьшается до предела, после которого задача теряет смысл, и т.п. Эти упрощения можно сделать при глубоком понимании сути задачи. На рис. 1.11,в приведен образец анализа правильности организа-ции цикла (верификация алгоритма).
1.3. Логические алгоритмы
Логическими принято называть алгоритмы, которые содержат пред-писания (операции) относительно объектов нечисловой природы. Харак-терной особенностью логических алгоритмов является выбор на каждом шаге по определенным правилам альтернативной операции, осуществля-емой при переходе к следующему шагу. К логическим задачам относят многие игры. Однако выделение логических задач из множества математи-ческих задач достаточно условно - в большинстве случаев задачи являются смешанными: в них присутствуют и числовые, и логические операции. Так, машинные алгоритмы игры в шахматы используют на каждом шаге вычис-ление значения некоторой функции, учитывающей оценку позиции после каждого следующего хода (точнее, полухода) и стоимость размена фигур.
Ниже рассматриваются две задачи, носящие выраженный логичес-кий характер.
1.3.1. Задача “Поиск пути в лабиринте”
Эта задача восходит к греческой мифологии, в которой, в частности, описывается подвиг Тезея, проникшего в лабиринт, где обитал чудовищный Минотавр (полубык, получеловек), пожиравший местных красавиц. Тезей разыскал в лабиринте Минотавра и убил его. Выбраться из лабиринта ему помогла Ариадна (А), дав ему вначале клубок ниток, один конец которых держала она сама. По мере углубления Тезея в лабиринт клубок разматы-вался; наматывая потом нитки, Тезей благополучно вернулся к выходу.
Рассмотрим задачу поиска пути в лабиринте в общем случае (для класса подобных задач) и приведём словесное описание алгоритма.
Представим лабиринт в виде конечной системы площадок, от кото-рых расходятся коридоры, причём каждый коридор соединяет две площад-ки (будем называть их смежными); возможно существование таких пло-щадок, из которых можно пройти только в один коридор (такие площадки будем называть тупиками). Геометрически лабиринт можно представить в виде системы точек А, В, С,..., изображающих площадки, и совокупности отрезков АВ, ВС,..., изображающих коридоры, которые соединяют опре-делённые пары данных точек (рис. 1.16). Смежными являются, например, площадки В и С, К и М и т. д., а тупиковыми - площадки А, D, I, J.
Рис. 1.16. Геометрическое представление лабиринта
Будем говорить, что площадка Y достижима из площадки X, если существует путь от X к Y через промежуточные коридоры и площадки. Точ-нее: либо X и Y - смежные площадки, либо существует последователь-ность площадок X1, X2,..., Xn таких, что X и X1, X1 и Х2..., и т.д., и, нако-нец, Xn и Y являются смежными. Отметим, что если Y достижима из X, то она достижима и посредством простого пути, т.е. такого пути, в котором каждая площадка (а тем более и каждый коридор) проходится лишь один раз. Например, путь ABCD является простым, а путь ABCFECD - нет.
Тезей должен был решить задачу: узнать, достижима ли площадка М, на которой находится Минотавр, из площадки А, на которой находится Ариадна, или нет? Если да, то к М можно было добраться по любому пути, но вернуться к площадке А нужно уже по простому пути. Поскольку заранее устройство лабиринта неизвестно, решение задачи должно быть представлено в виде общего метода поиска для любого лабиринта и при любом расположении площадок А и М, т. е. требуется построить алгоритм поиска пути в лабиринте.
Будем условно помечать коридоры следующими красками: непрой-денные ни разу - зелёной, пройденные один раз - жёлтой, пройденные дважды - красной.
Находясь на начальной площадке, Тезей может попасть на одну из смежных площадок посредством одного из следующих двух ходов:
1. Разматывание нити. Прохождение от данной площадки по любому зелёному коридору до смежной площадки. После прохождения этого коридора он считается жёлтым.
2. Наматывание нити. Возвращение от данной площадки по послед-нему пройденному жёлтому коридору до смежной площадки. При этом нить наматывается обратно на клубок, а этот коридор становится красным.
Предполагается, что Тезей делает какие-то пометки, позволяющие ему впоследствии отличать красные коридоры от зёленых; жёлтые разли-чимы тем, что по ним протянута нить Ариадны.
Обстановка на данной площадке характеризуется такими призна-ками.
1. Минотавр. Он обнаружен.
2. Петля. Через данную площадку уже протянута нить Ариадны (иначе: от данной площадки расходятся по крайней мере два жёлтых коридора).
3. Зелёная улица. От данной площадки есть вход по крайней мере в один зелёный коридор.
4. Ариадна. Она на данной площадке.
5. Особый случай. Отсутствие всех предыдущих признаков (например тупик).
Поставим в соответствие каждой обстановке на площадке свой ход.
| Признак | Ход |
| 1. Минотавр | Остановка |
| 2. Петля | Наматывание нити |
| 3. Зеленая улица | Разматывание нити |
| 4. Ариадна | Остановка |
| 5. Особый случай | Наматыване нити |
Находясь на некоторой площадке, Тезей делает очередной ход следующим образом: он проверяет по порядку номеров в соответствии с левым столбцом таблицы, какой из перечисленных признаков имеет место; обнаружив первый такой признак, он (уже не проверяя остальные признаки) делает соответствующий ход из правого столбца. Такие ходы делаются до тех пор, пока не наступит остановка.
Приведём (без доказательства) утверждения, которые являются обоснованием предложенного метода поиска пути в лабиринте.
1. При любом расположении А и М в лабиринте после конечного числа ходов обязательно наступит остановка либо на площадке Минотавра, либо на площадке Ариадны.
2. Если остановка наступила на М, то Минотавр достижим. Более того, в этом случае нить Ариадны оказывается протянутой по простому пути, ведущему от А к М. Наматывая нить, Тезей может теперь вернуться по этому пути к Ариадне.
3. Если остановка наступила на площадке Ариадны, то Минотавр не достижим.
Отметим, что в случае признака “зелёной улицы” ход не определён однозначно - нарушается свойство детерминированности алгоритма. Этот случай легко исправляется, если ввести дополнительное правило о том, что при наличии нескольких зелёных коридоров Тезей обходит площадку по часовой (против часовой) стрелке, выбирая очередной коридор. Ясно, что в общем случае алгоритм основан на переборе вариантов обхода площадок и коридоров.
1. 3.2. Задача “Ханойские башни”
Эта задача формулируется следующим образом. Имеется три стерж-ня, на одном из которых (назовём его занятым) находятся диски разных диаметров, расположенные на стержне в порядке убывания диаметров снизу вверх; второй стержень назовём свободным, а третий - вспомога-тельным (рис 1.17). Требуется, производя одиночные перемещения дисков, переместить всю “стопку” дисков с занятого стержня на свобод-ный, используя вспомогательный стержень; при этом на любом шаге диски должны быть расположены на каждом стержне в порядке убывания их диаметров.
Рис. 1.17. Ханойские башни
В табл. 1.5 приведен результат решения задачи для случая четырех дисков. Здесь А - занятый в начальный момент (нулевой шаг) стержень, В - свободный, а С - вспомогательный стержень. Цифрами обозначен “номер” диска, причём большему номеру соответствует больший диаметр. Отметим, что в середине процесса решения в качестве вспомогательного выступает то стержень А, то стержень С.
Видно, что процесс перемещения стопки дисков можно разбить на фазы (1-я фаза - шаги 1-8; 2-я фаза - шаги 9-12; 3-я фаза - шаги 13 и 14; 4-я фаза - шаг 15). К началу каждой фазы на вспомогательном (занятом) стержне собирается стопка дисков (в табл. 1.5 номера этих дисков подчёркнуты), затем в течение данной фазы самый нижний диск стопки перемещается на свободный стержень
Таблица 1.5.
| Шаг | ||||||||||||||||
| А | 4-1 | 4-2 | 4,3 | 4,3 | 4,1 | 4,1 | Æ | Æ | 2,1 | 2,1 | Æ | Æ | ||||
| В | Æ | Æ | 2,1 | 2,1 | Æ | Æ | 4,1 | 4,1 | 4,3 | 4,3 | 4-2 | 4-1 | ||||
| С | Æ | Æ | 3,2 | 3-1 | 3-1 | 3,2 | Æ | 1 | Æ |
Анализ перемещений дисков позволяет выявить определённые зако-номерности, составить словесное описание алгоритма перемещений для общего случая (количество дисков произвольно), а затем перейти к разра-ботке схемы алгоритма.
Чтобы переместить самый нижний диск на стержень В, необходимо 2n-1 перемещений. Общее число перемещений равно 2n-1.
Эти утверждения можно доказать по индукции.
Заключение
Любой вычислительный процесс может быть представлен компо-зицией следующих его фрагментов: линейный, ветвящийся, циклический.
Для организации разветвлений и циклов могут быть использованы различные операторы; выбор того или иного оператора в конкретном случае остаётся за программистом.
При организации разветвлений необходимо стремиться миними-зировать логическое выражение, описывающее выбор альтернатив.
При организации циклов особенно важны два момента: правиль-ное построение начала цикла и его конца. Важно также обеспечить стыковку цикла с остальной частью алгоритма или циклов друг с другом при их вложенности.
СА может быть представлена с разной степенью подробности. Так, предопределённый процесс, например блок ввода/вывода, может вклю-чать в себя несколько циклов; визуально фрагмент СА, включающий в себя этот блок, будет выглядеть линейным. В действительности линей-ными могут быть только очень простые алгоритмы или их некоторые фрагменты.
СА допускают эквивалентные преобразования, что может быть использовано для повышения эффективности алгоритмов. Например, имеет смысл выносить, если это возможно, из тела цикла все операторы, не связанные с параметром данного цикла.
Необходимо повышенное внимание уделять особым случаям, которые встречаются в данных либо в формулах (например, в алгоритме нахождения минимального числа множества - это случай, когда входное множество содержит один элемент либо оно пустое; при некоторых вычислениях возникает необходимость деления на 0 и т.п.).
Контрольные вопросы. Упражнения
1. Какие соединения вершин СА являются допустимыми? Предло-жите несколько вариантов произвольных СА, содержащих 8...10 вершин разных типов.
2. Вы сможете доказать, что каждый из рассмотренных в данной главе вычислительных процессов является алгоритмом?
3. Как надо скорректировать СА решения квадратного уравнения (рис 1.4), чтобы при преобразовании уравнения общего вида (1.7) к приведённому учесть случай а = 0 (при этом вычисление p и q связано с делением на 0, что недопустимо)?
4. Как изменится СА для процедуры MIN_A (пример 1.7), которая встроена в некий вычислительный процесс (модуль), если при обращении к этой процедуре возможны случаи, когда сформированный в основном процессе массив А содержит всего один элемент либо пуст?
5. Каким требованиям должны удовлетворять размерности матриц A, B и C, чтобы корректно выполнить матричную операцию D = A + B х C? Сколько циклов понадобится для вычисления матрицы D?
6. Почему некоммутативна в общем случае операция перемножения двух квадратных матриц одинаковой размерности? В каком частном случае коммутативность имеет место?
7. Составьте фрагменты СА для формул (1.16)... (1.19) и сравните попарно фрагменты для формул (1.16), (1.18) и (1.17), (1.19). В каком случае вычисления рациональнее и почему?
8. В чём отличие вариантов с использованием от вариантов без использования оператора case... of? Рассмотрите эти варианты для примера 1.5.
9. Чем отличаются операторы for, while … do, repeat … until?
10. Постройте схему алгоритма выбора, реализующую логическую функцию 
& 
, где B1, B2, B3 - некотоpые условия (булевы переменные).
Указание. Ввести промежуточную переменную 
& .
11. Постройте СА, реализующую предикат p(x) ï a£x<b.
Указание. Учесть, что предикат включает в себя 2 условия.
12. Составьте СА определения максимального элемента множества, содержащего 12 чисел. Какое количество сравнений и перестановок эле-ментов понадобится в случае, если массив отсортирован в порядке возра-стания элементов? Выведите формулу для определения количества срав-нений и перестановок в случае произвольного количества элементов.
13. Составьте словесное описание алгоритма перемножения двух матриц.
14. Для функции y=F(x), представленной разложением в ряд (1.20), постройте схему алгоритма, позволяющего вычислить значение y в точках разбиения с погрешностью e при равномерном разбиении области опре-деления функции [ a,b ] на m частей.
15. Составьте СА поиска пути в лабиринте.
16. Докажите, что в задаче “Ханойские башни” для перемещения n -го (самого нижнего) диска на свободный стержень необходимо 2 n-1 одиночных перемещений. Докажите также, что общее число перемещений на свобод-ный диск определяется числом 2 n -1.