Статистический критерий проверки нулевой гипотезы. Наблюдаемое значение критерия

Статистическая гипотеза. Нулевая и конкурирующая, простая и сложная гипотезы

Статистической называют гипотезу о виде неизвестного распределения, или о параметрах известных распределений.

Например, статистическими будут гипотезы:

1. генеральная совокупность распределена по закону Пуассона;

2. дисперсии двух нормальных совокупностей равны между собой.

Наряду с выдвинутой гипотезой рассматривают и противоречащую ей гипотезу. Если выдвинутая гипотеза будет отвергнута, то имеет место противоречащая гипотеза. По этой причине эти гипотезы целесообразно различать.

Нулевой (основной) называют выдвинутую гипотезу .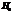

Конкурирующей (альтернативной) называют гипотезу 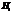которая противоречит нулевой.

Простой называют гипотезу, содержащую только одно предположение. Например, если — параметр показательного распределения, то гипотеза 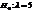— простая.

Сложной называют гипотезу, которая состоит из конечного или бесконечного числа простых гипотез. Например, сложная гипотеза 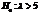состоит из бесчисленного множества простых вида 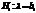, где 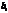— любое число, большее 5.

Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость ее проверки. Поскольку проверку производят статистическими методами, ее называют статистической. В итоге статистической проверки гипотезы в двух случаях может быть принято неправильное решение, т. е. могут быть допущены ошибки двух родов.

Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза.

Ошибка второго рода состоит в том, что будет принята неправильная гипотеза.

Вероятность совершить ошибку первого рода принято обозначать через ; ее называют уровнем значимости. Наиболее часто уровень значимости принимают равным 0,05 или 0,01. Если, например, принят уровень значимости равный 0,05, то это означает, что в пяти случаях из ста мы рискуем допустить ошибку первого рода (отвергнуть правильную гипотезу).

Статистический критерий проверки нулевой гипотезы. Наблюдаемое значение критерия

Для проверки нулевой гипотезы используют специально подобранную случайную величину, точное или приближенное распределение которой известно. Эту величину обозначают через U или Z, если она распределена нормально, F или — по закону Фишера — Снедекора, Т — по закону Стьюдента, — по закону «хи квадрат» и т. д. Поскольку в этом параграфе вид распределения во внимание приниматься не будет, обозначим эту величину, в целях общности, через К.

Статистическим критерием (или просто критерием) называют случайную величину К, которая служит для проверки нулевой гипотезы.

Для проверки гипотезы по данным выборок вычисляют частные значения входящих в критерий величин, и таким образом получают частное (наблюдаемое) значение критерия.

Наблюдаемым значением К_набл назначают значение критерия, вычисленное по выборкам.

Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают.

Областью принятия гипотезы (областью допустимых значений) называют совокупность значений критерия, при которых гипотезу принимают.

Критическими точками (границами) k_Kp называют точки, отделяющие критическую область от области принятия гипотезы.

Различают одностороннюю (правостороннюю или левостороннюю) и двустороннюю критические области.

Правосторонней называют критическую область, определяемую неравенством K>k_Kp, где k_Kp — положительное число

Левосторонней называют критическую область, определяемую неравенством K<k_Kp, где k_кр — отрицательное число.

Односторонней называют правостороннюю или левостороннюю критическую область.

Двусторонней называют критическую область, определяемую неравенствами , где .