Отыскание правосторонней критической области

Для отыскания правосторонней критической области достаточно найти критическую точку.

С этой целью задаются достаточно малой вероятностью — уровнем значимости . Затем ищут критическую точку k_Kp, исходя из требования, чтобы, при условии справедливости нулевой гипотезы, вероятность того, что критерий K примет значение, большее k_Kp, была равна принятому уровню значимости:

Отвергают гипотезу более категорично, чем принимают. Действительно, известно, что достаточно привести один пример, противоречащий некоторому общему утверждению, чтобы это утверждение отвергнуть. Если оказалось, что наблюдаемое значение критерия принадлежит критической области, то этот факт и служит примером, противоречащим нулевой гипотезе, что позволяет ее отклонить.

Отыскание левосторонней и двусторонней критических областей

Отыскание левосторонней и двусторонней критических областей сводится (так же, как и для правосторонней) к нахождению соответствующих критических точек.

Левосторонняя критическая область определяется неравенством .

Критическую точку находят, исходя из требования, чтобы при справедливости нулевой гипотезы, вероятность того, что критерий примет значение, меньшее , была равна принятому уровню значимости:

Двусторонняя критическая область определяется неравенствами

Критические точки находят, исходя из требования, чтобы, при справедливости нулевой гипотезы, сумма вероятностей того, что критерий примет значение меньшее или большее , была равна принятому уровню значимости:

Ясно, что критические точки могут быть выбраны бесчисленным множеством способов. Если же распределение критерия симметрично относительно нуля и имеются основания выбрать симметричные относительно нуля точки и (), то

.

24 .Сравнение двух дисперсий нормальных генеральных совокупностей

Пусть генеральные совокупности X и Y распределены нормально. По независимым выборкам объемов n₁ и n₂, извлеченным из этих совокупностей, найдены исправленные выборочные дисперсии и . Требуется по исправленным дисперсиям, при заданном уровне значимости , проверить нулевую гипотезу, состоящую в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой:

Учитывая, что исправленные дисперсии являются несмещенными оценками генеральных дисперсий т. е.

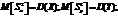
нулевую гипотезу можно записать так:

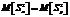
В качестве критерия проверки нулевой гипотезы о равенстве генеральных дисперсий, примем отношение большей исправленной дисперсии к меньшей, т. е. случайную величину

Величина F₁, при условии справедливости нулевой гипотезы имеет распределение Фишера—Снедекора со степенями свободы k₁=n₁-1 и k₂=n₂-1, где n₁— объем выборки, по которой вычислена большая исправленная дисперсия, n₂— объем выборки, по которой найдена меньшая дисперсия.

Напомним, что распределение Фишера—Снедекора зависит только от чисел степеней свободы и не зависит от других параметров.

.