Федеральное агентство по образованию
Государственное образовательное учреждение
Высшего профессионального образования
Санкт-Петербургский государственный горный институт им. Г. В. Плеханова
(технический университет)
Кафедра конструирования горных машин и
Технологии машиностроения
ТЕОРИЯ МЕХАНИЗМОВ И МАШИН
Методические указания по курсовому проектированию
САНКТ-ПЕТЕРБУРГ
УДК 621.01.001 (075.83)
ТЕОРИЯ МЕХАНИЗМОВ И МАШИН: Методические указания по курсовому проектированию / Санкт-Петербургский государственный горный ин-т.
Сост.: А.В. Большунов, В.В. Денегин, Г.В. Соколова. СПб, 2006. 27 c.
Изложены методические указания по выполнению курсового проекта и требования к его оформлению. Представлены типовые схемы механизмов с вариантами заданий для курсового проектирования по дисциплине «Теория механизмов и машин». Методические указания предназначены для студентов всех форм обучения специальностей 170100 (150402) «Горные машины и оборудование», 170300 (150404) «Металлургические машины и оборудование» и 090700 (130501) «Проектирование, сооружение и эксплуатация газонефтепроводов и газонефтехранилищ».
Научный редактор проф. И.П. Тимофеев
Библиогр.: 7 назв.
Ó Санкт-Петербургский горный
институт имени Г.В. Плеханова, 2006 г.
 |
ВВЕДЕНИЕ
Курсовое проектирование по теории механизмов и машин является заключительным этапом изучения дисциплины, способствующим закреплению, углублению и обобщению теоретических знаний, полученных студентами, и применению этих знаний к комплексному решению задачи динамического исследования механизма.
Курсовой проект содержит пояснительную записку и графические построения (схемы, чертежи). Графические построения к каждому разделу проекта выполняются на отдельных листах формата А1 с соблюдением всех требований ЕСКД. На чертежах следует сохранять все вспомогательные построения, проставлять принятые масштабы и соответствующие надписи. Каждый лист проекта должен иметь угловой штамп. Допускается компьютерный вариант выполнения чертежей с применением графических редакторов КОМПАС-3D.8V или AutoCAD 2005.
Пояснительная записка должна содержать титульный лист, аннотацию, содержание, список использованной литературы. В пояснительной записке следует привести схему механизма с исходными данными к проекту и расшифровкой обозначений величин.
Количество положений в цикле движения механизма следует принимать равным 12; для механизма четырехтактного двигателя внутреннего сгорания - 24. При выполнении расчетов следует записать исходную формулу, при необходимости преобразовать ее к удобному виду, подставить численные значения и указать результат. Обязательно указывать единицы измерения всех исходных и полученных в результате расчета величин. Расчеты для всех положений механизма рационально представлять в табличной форме.
Если студент ранее выполнял расчетно-графическую работу по кинематическому исследованию рычажного механизма, ее следует приложить к проекту и дать соответствующую ссылку в пояснительной записке.
При защите проекта студент, должен дать исчерпывающие объяснения по всем вопросам, связанным с методами исследования механизмов и приемами графических построений.
I. КИНЕМАТИЧЕСКОЕ ИССЛЕДОВАНИЕ
РЫЧАЖНОГО МЕХАНИЗМА
Целью кинематического исследования механизма является определение положений механизма в различные моменты времени, траекторий характерных точек звеньев механизма, включая центры масс звеньев, а так же величины и направления линейных скоростей и ускорений этих точек и угловых скоростей и ускорений звеньев.
Определение перечисленных кинематических характеристик производится в пределах одного периода (цикла) установившегося движения механизма, что соответствует одному полному обороту ведущего звена.
Кинематическое исследование механизма с одной степенью подвижности производят в предположении, что ведущее звено имеет постоянную угловую скорость.
В масштабе mS [м/мм] строят план 12 равноотстоящих по времени положений механизма за один цикл его работы. Масштаб плана положений принимают равным отношению
,
где O1A – действительная длина ведущего звена, м; O1A – чертежное изображение ведущего звена, принимаемое равным не менее 50 мм.
Нулевым (исходным) в цикле движения считают положение соответствующее началу холостого хода выходного звена механизма технологической машины или началу рабочего хода выходного звена энергетической машины. В тактах рабочего и холостого хода выделяют контурными линиями по одному положению механизма (номера положений студент выбирает самостоятельно).
В последовательности присоединения структурных групп и с учетом их особенностей графическим решением векторных уравнений скоростей и ускорений строят масштабные планы скоростей и ускорений. Планы скоростей строят для всех 12 фиксированных положений механизма, планы ускорений – для двух ранее выделенных. Для определения масштабных коэффициентов планов скоростей mu [м/(с×мм)] и планов ускорений ma [м/(с2×мм)] задают изображения линейной скорости и ускорения кривошипной точки ведущего звена не менее 50 мм.
По построенным планам вычисляют линейные скорости и ускорения для всех характерных подвижных точек звеньев механизма, включая центры масс звеньев, а также угловые скорости и ускорения звеньев. Результаты вычислений представляют в табличной форме.
Планы скоростей и ускорений оформляют на чертеже как отдельные изображения с подрисуночными надписями с обязательным указанием соответствующих масштабных коэффициентов mS, mu и ma.
По результатам решений планов скоростей строят масштабный график скоростей выходного звена механизма за цикл движения. При этом в такте холостого хода скорости выходного звена принимают направленными вверх, а в такте рабочего хода – вниз.
График перемещений выходного звена в функции угла поворота кривошипа строят методом графического интегрирования графика скоростей. При этом площадь между кривой скоростей и осью абсцисс на каждом участке интегрирования заменяют равновеликим прямоугольником. Получаемые горизонтальные стороны сносят на ось ординат и из точек пересечения проводят лучи в полюс интегрирования, расположенный на продолжении оси абсцисс. На поле графика перемещений последовательно пристраивают хорды будущей кривой на интегрируемых участках, параллельные соответствующим лучам, проведенным в полюс интегрирования скоростей. По полученным точкам строят лекальную кривую графика перемещений. При этом масштабный коэффициент графика перемещений mS [м/мм] вычисляют по следующей зависимости:
,
где h1 – полюсное расстояние для интегрирования, мм; mu – масштабный коэффициент графика скоростей, м/(с×мм); mt – масштабный коэффициент времени, с/мм.
где w – заданная угловая скорость ведущего звена, с-1; t – время цикла работы механизма, с;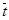 
– чертежное изображение времени цикла работы механизма, мм. Значение 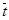принимают кратным 12 (180 мм, 240 мм и т.п.).
График ускорений получают методом графического дифференцирования скоростей выходного звена. Для чего на каждом участке дифференцирования проводят хорды кривой скорости. На продолжении оси абсцисс будущего графика ускорений откладывают полюсное расстояние h2 [мм]. Из полученного полюса проводят лучи параллельные соответствующим хордам графика скоростей. Через точки пересечения лучей с осью ординат на каждом участке проводят отрезки параллельные оси абсцисс и далее проводят окончательную кривую ускорения выходного звена.
Масштабный коэффициент ускорений ma [м/(с2×мм)] определяют из метрического соответствия графиков скоростей и ускорений
.
Для двух выбранных в кинематическом исследовании положений механизма по полученным графикам вычисляют перемещения и ускорения выходного звена, которые сравнивают с соответствующими перемещениями и ускорениями, рассчитанными по планам положений и ускорений, и оценивают погрешность вычислений в процентах.
II. ДИНАМИЧЕСКОЕ ИССЛЕДОВАНИЕ ДВИЖЕНИЯ СИСТЕМЫ
Для определения истинного закона движения механизма достаточно установить закон движения ведущего звена механизма под действием заданных сил и моментов сил. При этом действующие силы и моменты, а также массы и моменты инерции звеньев следует привести к ведущему звену механизма, называемому звеном приведения.
Уравнение приведенного момента сил сопротивления или движущих сил (в зависимости от типа машины) с учетом сил тяжести звеньев в общем виде в каждом расчетном положении имеет вид
,
где MC – приведенный момент сил сопротивления, Нм; MД – приведенный момент движущих сил, Нм; j – угол положения начального звена; i – номер звена; Fi – сила сопротивления (FС) или движущая сила (FД), Н;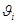 
– скорость точки приложения силы Fi, м/c; a i – угол между линией действия силы Fi и вектором скорости ; 
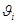– скорость кривошипной точки A, м/с; lOA – радиус кривошипа, м; Gi – сила тяжести i -го звена, Н; 
– линейная скорость центра масс i -го звена, м/с.
Для упрощения расчетов рационально в представленном уравнении заменить линейные скорости (, , 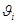) их изображениями на планах скоростей. Тогда расчетные формулы приведенного момента сил сопротивления MC или движущих сил MД имеют вид
,
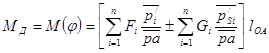
где 
, 
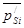– чертежные изображения проекций векторов скоросте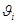й и на линии действия соответствующих сил на плане скоростей, мм; 
– чертежное изображение вектора скорости кривошипной точки А на плане скоростей, мм.
Окончательный вид расчетной формулы определяется схемой механизма и исходными данными к ней.
В расчетах приведенного момента сил сопротивлений при составляющих от сил тяжести знак «плюс» соответствует положениям механизма, в которых вертикальные проекции скоростей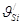 
направлены вверх, а знак «минус» – при направлении этих проекций вниз. В расчетах приведенного момента движущих сил знаки при составляющих от сил тяжести противоположны предыдущим: плюс при направлении векторов 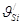вниз и минус, если эти векторы направлены вверх.
Рассчитывают МС (МД) за цикл движения механизма. По результатам вычислений в масштабе mM [Нм/мм] строят график моментов сил сопротивлений или движущих сил M = f(j).
Интегрированием графика приведенного момента сил в функции угла положения начального звена получают масштабный график работ приведенных сил A = f(j). Интегрирование выполняют ранее освоенным методом хорд, при этом предварительно задаются величиной полюсного расстояния h [мм]. Масштабный коэффициент mA [Дж/мм] графика работ вычисляют по зависимости
где h – полюсное расстояние, мм; mM – масштабный коэффициент графика моментов сил, Нм/мм; mj – масштабный коэффициент углов положения начального звена, рад/мм.
,
где 
– чертежное изображение угла поворота кривошип, мм. Принимают равным значению кратному 12 (180 мм, 240 мм и т.п.).
Учитывая, что за цикл установившегося движения системы сумма работ сил сопротивлений и движущих сил равна нулю, строят прямолинейный график работ движущих сил AД = f(j) для технологической машины или график работ сил сопротивлений AС = f(j) для энергетической машины.
Алгебраическим суммированием ординат графиков работ сил сопротивлений AС = f(j) и движущих сил AД = f(j) строят масштабный график избыточной энергии D T = f(j) рассматриваемой системы. При этом масштабный коэффициент m D T [Дж/мм] графика D T = f(j) принимают равным масштабному коэффициенту графика работ mA. Если амплитуда графика D T = f(j) оказывается незначительной, то масштабный коэффициент следует уменьшить в 2÷3 раза и принять его равным m D T = mA/(2÷3).
Для всех положений механизма за цикл движения рассчитывают избыточную энергию D T [Дж], равную
,
где 
– изображение избыточной энергии на графике D T = f(j), мм.
Результаты вычислений D T за цикл движения механизма следует представить в табличной форме.
Составляют расчетную формулу приведенного к начальному звену момента инерции системы в функции угла положения. Окончательный вид расчетной формулы зависит от схемы механизма и исходных данных к ней.
Приведенный момент инерции системы равен
,
где Jc – постоянная часть приведенного момента инерции, кг×м2; Jv – переменная часть приведенного момента инерции, кг×м2.
,
где J01 – момент инерции начального звена относительно оси, проходящей через его центр масс, кг×м2; JДВ – момент инерции ротора двигателя, кг×м2; w1 – угловая скорость начального звена, с-1; wДВ – угловая скорость ротора двигателя, с-1.
,
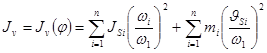где JSi – момент инерции i -го звена относительно оси, проходящей через центр масс звена, кг×м2; wi – угловая скорость i -го звена, с-1; mi – масса i -го звена, кг; – линейная скорость центра масс i -го звена, м/с.
Рассчитывают приведенный момент инерции системы за цикл движения механизма. По результатам вычислений в масштабе mJ [кг×м2/мм] строят график приведенного момента инерции системы в функции угла положения начального механизма J = f(j).
Учитывая последующую необходимость исключения углового параметра j, оси координат графика J = f(j) располагают повернутыми на 900 по часовой стрелке с размещением его на чертеже вверху справа от сетки предыдущих графиков M = f(j), A = f(j), D T = f(j).
Решением дифференциального уравнения движения системы получают расчетную формулу скорости начального звена в функции угла положения
,
где w – угловая скорость начального звена в каждом расчетном положении механизма, c-1; J0 – приведенный момент инерции системы в начале цикла, кгм2; w0 – угловая скорость звена приведения в начале цикла, с-1; Ji – приведенный момент инерции системы в каждом расчетном положении, кгм2.
По результатам вычислений строят масштабный график угловой скорости звена приведения w = f(j), рассчитывают среднюю скорость wср за цикл движения и определяют фактический коэффициент неравномерности движения d системы
,
где wmax – максимальная скорость ведущего звена, с-1; wmin – минимальная скорость ведущего звена, с-1; wср – средняя скорость ведущего звена, с-1.
Если расчетный коэффициент неравномерности оказывается больше заданного допустимого значения, следует перейти к проектированию маховика – регулятора движения системы.
Проектирование маховика – регулятора
Движения системы
Совместным решением зависимостей D T = f(j) и J = f(j) при исключении углового параметра j получают функцию D T = f(J), графически представляемую диаграммой Ф. Виттенбауэра (кривая энерго-масс).
При заданной средней скорости звена приведения рассчитывают углы наклона ymin и ymax внешних касательных к указанной кривой
,
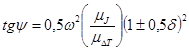где mJ – масштабный коэффициент момента инерции, кг×м2/мм; m D T – масштабный коэффициент энергии, Дж/мм; d – заданный коэффициент неравномерности движения.
Знак «плюс» используют при расчете ymax, знак «минус» – ymin.
К кривой Ф. Виттенбауэра строят внешние касательные с наклонами к оси моментов инерции под углами ymax и ymin.
На оси D T определяют отрезок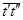 
, являющийся изображением в мм части избыточной энергии аккумулируемой маховиком. Момент инерции маховика Jм [кг×м2] определяют по зависимости
,
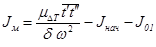где Jнач – момент инерции системы в начале цикла, кг×м2; J01 – момент инерции кривошипа, кг×м2.
Далее выделяют часть момента инерции моховика, относящуюся к его ободу Jоб = (0,85…0,95)Jм и рассчитывают размеры поперечного сечения обода.
Расчетный диаметр маховика в первоначальном варианте принимают равным Dм = 10lOA.
Масса обода маховика mоб [кг]
,
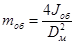С учетом принятого диаметра Dм и удельного веса материала маховика r масса обода маховика равна
,
где b – ширина обода маховика, м; h – высота обода маховика, м; r – удельный вес материала маховика (для серого чугуна r = 7100 – 7300 кг/м3).
Отношение b/h принимают равным 1,4…1,6.
В полученные размеры сечения обода вносят коррективы изменением диаметра Dм. Следует рассмотреть несколько вариантов (2 ¸ 3) и принять оптимальный.
При этом следует проверить маховик на непревышение его ободом критической скорости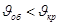 
. Для серого чугуна критическая скорость равняется 
.
