Тема: «Системы линейных алгебраических уравнений».
Составила: студентка 1-ого курса
ИрГУПС, группа Э-09-11-1
С.С.Сергина
Р.Р.Казарова
Под редакцией профессора
В.К.Турчанинова
г.Северобайкальск.2011г.
Системы линейных алгебраических уравнений.
Основные понятия:
Системой линейных алгебраических уравнений, содержащей m-уравнений и n-неизвестных, называется система вида:

Числа 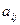 называются коэффициентами системы. Числа
называются коэффициентами системы. Числа 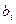 – свободными членами. Нахождению подлежат неизвестные
– свободными членами. Нахождению подлежат неизвестные 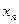 .
.
Основной матрицей данной системы называется матрица, состоящая из коэффициентов, вида: 
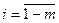 ,
, 
Расширенной матрицей 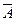 называется основная матрица данной системы, дополненная столбцом из свободных членов:
называется основная матрица данной системы, дополненная столбцом из свободных членов:

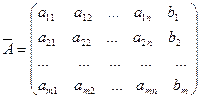
Система уравнений называется совместной, если она имеет хотя бы одно решение.
Несовместная система не имеет ни одного решения.
Совместная система называется определенной, если она имеет единственное решение.
Неопределенная система имеет более одного решения.
Каждое из её решений носит название частного решения. Совокупность всех частных решений даёт общее решение.
Решить систему, значит определить, в первую очередь, совместна ли она или несовместна. Если система совместна, то
тогда найти её общее решение.
Теорема Кронекера-Капелли.
- Совместность системы.
Пусть дана произвольная система линейных уравнений числом m- и n- неизвестными.
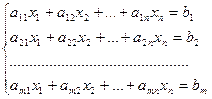
Исчерпывающий ответ на вопрос о совместности этой системы дает нам теорема Кронекера-Капелли.
Её суть: система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу её основной матрицы:rangA=rang 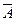
Практически полезное правило, позволяющее разыскивать все решения линейной системы уравнений формулируется следующим образом: если ранг совместной системы равен числу неизвестных, то система имеет единственное решение.
Второе полезное правило: если ранг системы(совместной) меньше числа неизвестных, то система имеет бесконечное множество решений.
Алгоритм решений произвольной системы линейных уравнений:
1. Найти ранг основной и расширенной матрицы исследуемой системы. Если rang 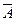 =rangA, то система совместна. В противном случае она несовместна.
=rangA, то система совместна. В противном случае она несовместна.
2.Если система совместна, нужно найти какой-либо базисный минор порядка r. Взять r уравнений, из коэффициентов которых составлен базисный минор. Неизвестные, коэффициенты которых составляют базисный минор, носят название главных. Остальные n-r неизвестных называются свободными и переносятся в правые части уравнений.
3.Найти выражение главных неизвестных через свободные, получив тем самым общее решение.
4.Придавая свободным неизвестным произвольные значения, получить соответствующие значения главных неизвестных. Таким образом находятся частные решения исходной системы линейных уравнений.
Примеры:
№1
Показать, что эта система совместна, используя теорему Кронекера –Капелли:
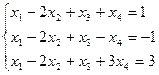
Решение:
Система линейных алгебраических уравнений совместна, если ранг расширенной матрицы равен рангу основной матрицы, т.е., rang 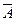 =rang A.
=rang A.
- Составим основную и расширенную матрицу данной системы:
 основная матрица данной системы
основная матрица данной системы
 расширенная матрица данной системы
расширенная матрица данной системы
- Найдём ранг основной матрицы(rangA). Для этого запишем определители третьего порядка, поскольку матрица содержит три строки. Таких определителей – четыре
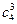
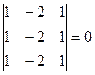
Так как определитель, имеющий 2 одинаковых ряда равен 0.

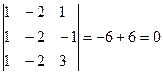
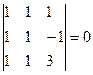 -( по свойству определителей)
-( по свойству определителей)
Все определители третьего порядка равны нулю, поэтому найдём миноры 2-го порядка.
Общее число таких миноров- восемнадцать 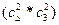 . Найдем среди них хотя бы несколько не равных нулю:
. Найдем среди них хотя бы несколько не равных нулю:

Видно, что среди них есть не равные нулю миноры.
Значит rangA=2.
3. Теперь найдем rang 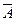 .Так как матрица имеет три строки, ищем миноры третьего порядка. Их общее число – десять
.Так как матрица имеет три строки, ищем миноры третьего порядка. Их общее число – десять 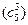
 - ( определители, имеющие 2 одинаковых ряда, равны 0.)
- ( определители, имеющие 2 одинаковых ряда, равны 0.)
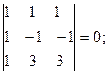
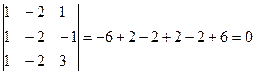
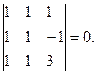 - ( для определителей с двумя одинаковыми рядами)
- ( для определителей с двумя одинаковыми рядами)

Так как миноры 3-го порядка равны нулю, то найдем, не равные нулю, миноры 2-го порядка. Таких миноров – тридцать  Среди них есть не равные нулю:
Среди них есть не равные нулю:


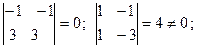
Значит rang 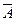 =2
=2
Вывод: Так как rang A=2, то, по теореме Кронекера - Капелли, исследуемая система совместна.
№2
Исследовать на совместимость, приведенную ниже систему:

Решение:
1. Составим основную и расширенную матрицы:


2. Для определения rang A и системы в целом вычислим миноры 3-го порядка основной матрицы и выявим среди них не равные нулю, если таковых нет, аналогично исследуем миноры 2-го порядка:
Общее число миноров третьего порядка десять 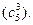
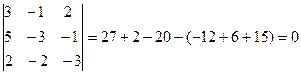
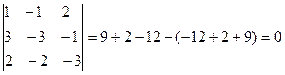
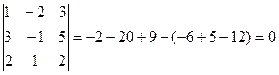
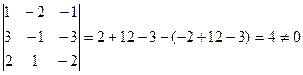
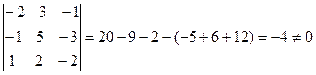
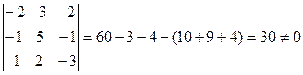
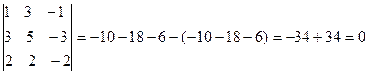


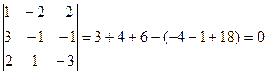
rang A=3
Есть отличные от нуля, миноры третьего порядка. Найдем несколько, не равных нулю, миноров второго порядка. Их общее число – тридцать 
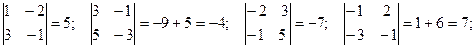
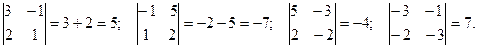
Есть отличные от нуля миноры второго порядка, следовательно rang A=2
3. Теперь найдём миноры третьего порядка расширенной матрицы. Их общее число- двадцать 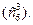
Поэтому отыщем несколько таких миноров, не равных нулю:

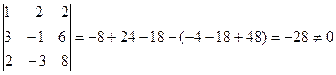
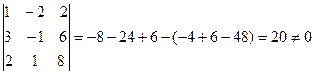
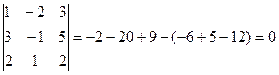
Есть отличные от нуля миноры третьего порядка, следовательно, rang  =3
=3
Вывод: Так как rang  =rang A,то, по теореме Кронекера- Капели(системы линейных алгебраических уравнений совместна только тогда, когда rang A=rang
=rang A,то, по теореме Кронекера- Капели(системы линейных алгебраических уравнений совместна только тогда, когда rang A=rang 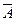 ), эта система несовместна.
), эта система несовместна.
№3
Исследуйте на совместимость, ниже приведенную систему, используя теорему Кронекера – Капелли:

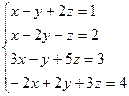
Решение:
По теореме Кронекера – Капелли система совместна только тогда, когда rang A=rang 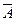
Находим rang A и rang 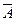 и затем исследуем на совместимость систему.
и затем исследуем на совместимость систему.
1. Запишем основную и расширенную матрицу:
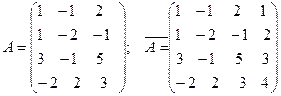
2. Вичислим миноры основной матрицы. Она имеет три столбца, поэтому в первую очередь ищем определители третьего порядка. Их общее число- четыре 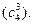

Все миноры третьего порядка не равны нулю.
Значит rang A=3.
3. Для определения rang 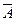 Вычислим миноры расширенной матрицы. Она имеет четыре строки и столбца. Поэтому в первую очередь вычислим её определитель четвертого порядка:
Вычислим миноры расширенной матрицы. Она имеет четыре строки и столбца. Поэтому в первую очередь вычислим её определитель четвертого порядка:
det A= 
Он не равен нулю. Значит rang 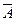 =4.
=4.
Вывод: Так как rangA  rang
rang 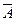 , то по теореме Кронекера – Капелли, эта система несовместна.
, то по теореме Кронекера – Капелли, эта система несовместна.
Задание для самостоятельной работы:
Показать, что система совместна(или несовместна)используя теорему Кронекера – Капелли:
№1
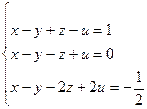
Ответ: система совместна.
№2
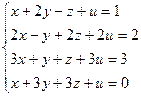
Ответ: система совместна.
№3

Ответ: система несовместна.
№4
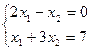
Ответ: система совместна
№5
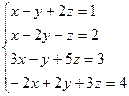
Ответ: система совместна.