Конечные функциональные преобразователи
Конечные функциональные преобразователи
Пусть
А – некоторое множество элементов информации, представленных тем или иным образом;
В – другое множество элементов информации;
Ф – функция преобразования.
Преобразователь информации можно представить себе схематично как устройство, реализующее отображение Ф:А→В одного множества в другое.
Решение задачи построения таких преобразователей для множеств А и В произвольной природы достаточно трудное, т.к. о самом отображении Ф ничего
| Ф |
| В |
| А |
не известно. Однако, если А и В являются конечными (т.е. преобразователь, который хотим построить, явлется «конечным функциональным преобразователем») и дискретными (т.е. преобразования осуществляются в дискретные моменты времени), существует систематический метод решения этой задачи. Он состоит в том, что элементы множеств А и В предварительно кодируют двоичными кодами и строят преобразование одного множество двоичных векторов в другое.
При таком подходе проблема реализации преобразователя Ф сводится к построению 3-х преобразователей:
К: А→Х – кодировщика;
F: X→Y – функционального преобразователя;
D: Y→B - декодировщика.
Причём отображения К, F, D должны быть выбраны так, чтобы реализовывать Ф, т.е. КºFºD=Ф.
| K |
| Х |
| А |
| F |
| Y |
| D |
| B |
| . . . |
| . . . |
Двоичное кодирование состоит во взаимно однозначном сопоставлении всем всем элементам коне- исло элементов множествачного множества некоторых двоичных векторов одной и той же длины.
Если  - число элементов множества А,
- число элементов множества А,  - число векторов длины
- число векторов длины  , то для однозначности кодирования
, то для однозначности кодирования  .
.
Предположим, что  ,
,  , тогда
, тогда  и
и 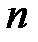 - длины двоичных векторов для кодирования множеств А и В соответственно. Если Ф:А→В, то проблема реализации преобразователя Ф сводится к построению:
- длины двоичных векторов для кодирования множеств А и В соответственно. Если Ф:А→В, то проблема реализации преобразователя Ф сводится к построению:
- устройства кодирования
 ,
,
которое взаимно однозначно преобразовывает элементы информации множества А в двоичные вектора длины  ;
;
- функционального преобразователя
 ;
;
- устройства декодирования
 ,
,
которое взаимно однозначно преобразовывает двоичные векторы длины 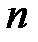 в элементы информации множества В.
в элементы информации множества В.
Таким образом, проблема построения конечного функционального преобразователя Ф сводится к реализации произвольного преобразователя  , который может быть задан, например, таблично.
, который может быть задан, например, таблично.
Пример. Пусть  ,
,  . Отображение Ф:А→В задано таблицей
. Отображение Ф:А→В задано таблицей
| А | 
| 
| 
| 
| 
|
| В | 
| 
| 
| 
| 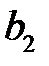
|
В этом случае 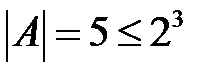 ,
,  , следовательно,
, следовательно,  ,
,  . Произвольно выбираем функции кодирования и декодирования:
. Произвольно выбираем функции кодирования и декодирования:

| А | 
| 
| 
| 
| 
|

|


| ||||
| В | 
| — | 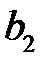
| 
|
Отображение F строим таким образом, чтобы отношение КºFºD=Ф выполнялось.
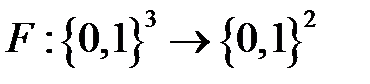
| А | 
| 
| В |
| — | — | — | |

| 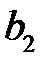
| ||

| 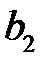
| ||

| 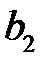
| ||

| 
| ||
| — | — | — | |

| 
| ||
| — | — | — |
В результате, проблема построения произвольного преобразователя 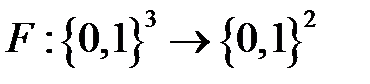 теперь имеет более чёткую математическую формулировку. Для решения этой задачи используют следующий приём: вместо одной функции
теперь имеет более чёткую математическую формулировку. Для решения этой задачи используют следующий приём: вместо одной функции 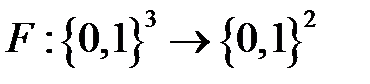 строят 2 булевы функции
строят 2 булевы функции  ,
,  , таким образом, чтобы реализациясовокупности этих более простых функций давала искомый преобразователь
, таким образом, чтобы реализациясовокупности этих более простых функций давала искомый преобразователь  . Для рассматриваемого примера имеем:
. Для рассматриваемого примера имеем:

| 
| 
|
| — | — | |
| — | — | |
| — | — |
Схема отображения имеет три двоичных входа и два двоичных выхода:
| F |
| f2 |
| x |
| y |
| z |
| f1 |
Здесь  и
и  неполностью определённые булевы функции, которые представляют соответствующие разряды результата отображения
неполностью определённые булевы функции, которые представляют соответствующие разряды результата отображения  . чтобы найти минимальные ДНФ этих фунций надо заменить их подходящими полностью определёнными булевыми функциями. Для этого используют карты Карно для
. чтобы найти минимальные ДНФ этих фунций надо заменить их подходящими полностью определёнными булевыми функциями. Для этого используют карты Карно для  и
и  , в которых неопределённые значения заменяют 0 или 1, чтобы покрыть таблицы минимальным числом максимальных прямоугольников и получить минимальные ДНФ уже определённых функций.
, в которых неопределённые значения заменяют 0 или 1, чтобы покрыть таблицы минимальным числом максимальных прямоугольников и получить минимальные ДНФ уже определённых функций.
Для функции  имеем:
имеем:

 .
.
Для функции  получим:
получим:

 .
.
Система  полностью определённых булевых функций есть отображение
полностью определённых булевых функций есть отображение 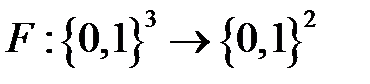 .
.