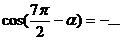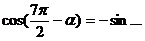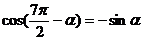Радианы
Углы измеряются не в градусах, а в радианах, Радиан – это такой угол, что дуга единичной окружности равна радиусу (то есть 1). Это примерно 57 градусов. Половина окружности (180 °) – это π радиан. (π≈3.14159)
Пример 1: перевести в радианы 30 °
| Пример 2: перевести в градусы π/9 радиан
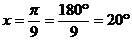
|
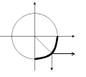
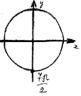
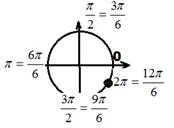
| Как найти на единичной окружности угол в радианах | Пример: найти точку, соответствуюшую углу 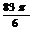
| ||
| Если число большое, то: 1) Делим нацело 2) Убираем полные обороты (четное количество «пи») 3) Если осталось «пи», приводим к общему знаменателю |  = = 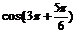 = = 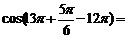 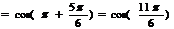
| ||
| 4) Подписываем точка на координатных осях, и приводим их к этому же знаменателю 5) И наконец находим нужную точку Внимание! Если есть «минус», откладываем углы в другую сторону! |
|
Синусы и косинусы, тангенсы и котангенсы
 Синус угла - это ОРДИНАТА (кордината по У) соответств. точки единичной окружности.
Синус угла - это ОРДИНАТА (кордината по У) соответств. точки единичной окружности.
Косинус угла - это АБСЦИССА (коорд по Х) соответств. точки единичной окружности.
Тангенс – это синус, деленный на косинус: 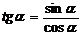
Котангенс – это косинус, деленный на синус: 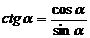 ;
; 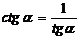
Если точка попадает на горизонтальную ось, то синус равен нулю, а котангенс не существует. Если на вертикальную ось, то косинус равен нулю, а тангенс не существует.
И еще надо знать ОСНОВНОЕ ТРИГОНОМЕТРИЧЕСКОЕ ТОЖДЕСТВО: 
Значения синусов, косинусов, тангенсов и котангенсов для «хороших» углов
| Угол в град | Запоминать надо только значения синусов. Значения косинусов пишутся «наоборот» - справа налево. Значения тангенса можно получить, если синус разделить на косинус; котангенса – если косинус разделить на синус.
Если значения синусов не запомнить, можно поступить так: во всех клетках таблицы нарисовать дроби со знаменателем 2, а в числителе – корни из чисел 0,1,2,3,4:
Дальще надо сосчитать те корни, которые можно, и получится строчка для синусов | |||||||||||||||||
| Угол в радианах | 
| 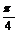
| 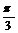
| 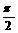
| ||||||||||||||
| Синус | 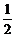
| 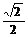
| 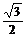
| |||||||||||||||
| Косинус | 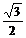
| 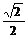
| 
| |||||||||||||||
| Тангенс | 
| 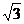
| Не сущес-твует | |||||||||||||||
| Котангенс | Не сущес-твует | 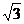
| 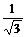
|
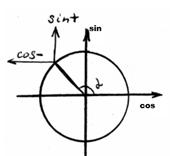 4. Знаки синуса, косинуса, тангенса, котангенса
4. Знаки синуса, косинуса, тангенса, котангенса
Знаки опеделяем так: из заданной точки рисуем вертикальную и горизонтальную стрелки наружу. Если направление стрелки совпадает с направлением оси координат, то соответствующая тригонометрическая функция (синус или косинус) имеет знак «плюс», иначе знак «минус». Знаки тангенса и котангенса (всегда одинаковые) определяются с учетом того, что надо синус делить на косинус.
Пример: Для точки, показанной на рисунке, синус положительный (стрелка вверх, совпадает с направлением оси игреков), косинус отрицательный (стрелка влево, противоположна направлению оси иксов), тангенс и котангенс отрицательные («плюс» делить на «минус»)
Как по одной тригонометрической функции найти все остальные
| Как найти одн тригонометрическую функцию по другой (тангенс по синусу или косинусу и т.д.) | Найти 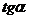 , если , если 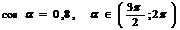
| ||
| 1) Представляем заданную величину в виде простой дроби. 2) Рисуем прямоугольный треугольник, отмечаем дужкой любой острый угол и подписываем стороны, равные числителю и знаменателю дроби (по определению) |
| ||
| 3) По теореме Пифагора находим третью сторону |  , значит, х=6 , значит, х=6
| ||
| 4) По треугольнику находим нужную тригонометрическую функцию | Тангенс – это отношение противолежащего катета к прилежащему, значит, 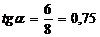
| ||
| 5) На единичной окружности обводим дугу, которой принадлежит угол. Определяем на нем знак найденной тригонометрической функции 6) Пишем ответ |
|
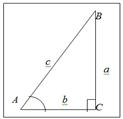
| Определения синуса, косинуса, тангенса и котангенса из прямоугольного треугольника | |
Синус – отношение противолежащего катета к гипотенузе 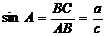 Косинус – отношение прилежащего катета к гипотенузе
Косинус – отношение прилежащего катета к гипотенузе 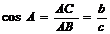 Тангенс – отношение противолежащего катета к прилежащему:
Тангенс – отношение противолежащего катета к прилежащему: 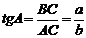 .
Котангенс – отношение прилежащего катета к противолежащему: .
Котангенс – отношение прилежащего катета к противолежащему:  . .
| 
|
Формулы приведения
| Как выразить тригонометрические функции любого угла через тригонометрические функции острого угла | Пример: Упростить 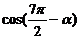
| |||
| 1) Находим на единичной окружности «опорную точку» - которая в формуле задана числом; эта точка должна попасть на одну из координатных осей 2) Откладываем от нее в нужном направлении острый угол α 3) Определяем знак заданной тригонометрической функции, записываем его 4) Если опорная точка попадала на вертикальную ось (то есть угол α откладывался от вертикальной оси), то вместо косинуса пишем синус, вместо тангенса котангенс, и наоборот (меняем тригонометрическую функцию). А если опорная точка попадала на горизонтальную ось, пишем ту же тригонометрическую функцию, что была в задании (не меняем) (это «правило лошади» J) 5) А в качестве аргуметра функции пишем просто угол α |
4) 5)
|
С помощью формул приведения можно найти синусы, косинусы, тангенсы, котангенсы для тупых углов, например: 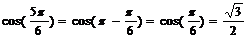
Примечание: если в задании есть два «нехороших» угла, можно с помощью формул приведения попытаться выразить один через другой, например: 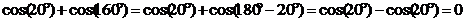
Полезно запомнить следующие частные случаи формул приведения:
1) 
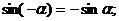
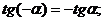
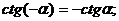
(у косинуса знак убирается, у остальных тригонометрических функций выносится вперед)
2) Полные обороты убираются! То есть, например, 
(полный оборот – это четное число, умноженное на π)
3) 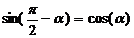 , а также
, а также  ;
; 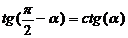 ;
; 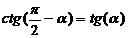 ,
,
(если два угла в сумме составляют 90° (или π/2), то их тригонометрические функции меняются местами, например
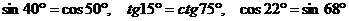 )
)
| Как боротья с большими углами в градусах | Пример: Вычислить 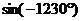
|
| 1) Убираем минус, если есть | У синуса минус выносится вперед: 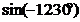 =- =- 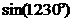
|
| 2) Убираем полные обороты (четное количество пи) (можно вычитать 360 или 3600 и т.д., пока не получим число меньше 360) | - 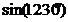 = = 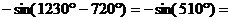

|
| 3) Представляем получившийся угол как сумму «опорной точки» и острого угла и считаем по формулам приведения | 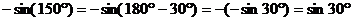 = = 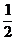
|
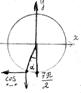
| Как боротья с очень большими углами в радианах | Пример: Вычислить 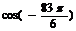
|
| 1) Убираем «минус», если есть | У косинуса минус пропадает: 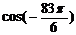 = = 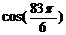
|
| 2) Убираем полные обороты – как это делается, см. §2 – «Радианы» | 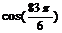 = = 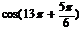 = = 
|
| 3) Представляем получившийся угол как сумму «опорной точки» и острого угла и считаем по формулам приведения | 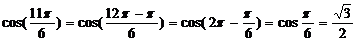
|
Примечание: если сделать п.3 никак не получается, то можно представить угол, получившийся в п.2, в градусах:
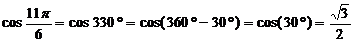
|
Формулы двойного угла
Синус двойного угла 
Пример: 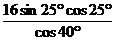 ==
== 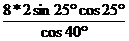 =
= 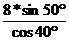 =
=  =
= 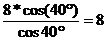
Косинус двойного угла 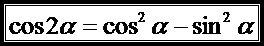
Пример: Найти  (15 градусов – это половина от 30, используем формулу двойного угла):
(15 градусов – это половина от 30, используем формулу двойного угла):
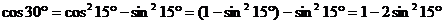 ,,
,, 
Тангенс двойного угла 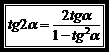
Пример: Найти 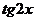 , если
, если 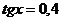 Решаем по формуле:
Решаем по формуле: 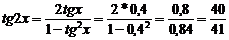 ;
;
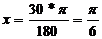
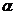
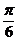
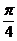

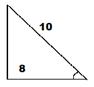
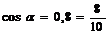 косинус – это отношение прилежащего катета к гипотенузе, значит, 10 – гипотенуза, 8 – прилежащий катет
косинус – это отношение прилежащего катета к гипотенузе, значит, 10 – гипотенуза, 8 – прилежащий катет