В этом случае одна опора становится шарнирно-подвижной. Недостающая связь устанавливается как внутренняя и соединяет диски. Примеры трёхшарнирных систем с затяжкой показаны на рис.1.28.

 | |||||||
 | |||||||
 | |||||||
| |||||||
Кинематический анализ производится по следующей схеме.
1. Определяется число степеней свободы по формуле (1.1) Здесь число Дисков (Д) = 3, Число шарниров (Ш) = 3. Опорных связей (С0) = 3. Подставив в формулу, получим W=3*3-2*3-3 =0
Вывод: возможно, что система СО и ГН.
 | |||
| |||
параллельны между собой. Система в целом является СО и ГН.
Пример 1.3. Кинематического анализа составной статически определимой балки (рис. 1.30)
 | |||
|
1. Подсчитываем число степеней свободы по выражению (1.1). Число дисков (Д) – 5; шарниров (Ш) – 4; число опорных связей (С0) – 7.
Тогда W=3*5-2*4-7=0
Вывод: Возможно, система СО и ГН.
2. Выполняем анализ балки по её образованию. При этом землю принимаем за дополнительный диск.
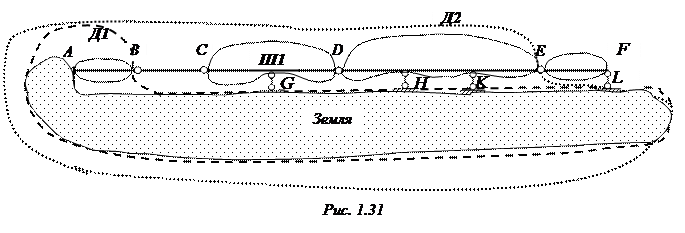
Выделим диски, на которые делится сама балка (AB, CD, DE,EF) и диск-Землю. Соединения этих дисков должны хорошо просматриваться. Это опорные связи (G,H,K,L), шарнир (D). Диск BC также принимаем за связь, так как он связывает между собой два диска (AB и CD) и не связан с землёй.
Рассмотрим теперь соединения этих дисков. Будем укрупнять их, пока не докажем, что вся балка является диском. Напомним, что диском называется часть системы или вся система целиком, если её геометрическая неизменяемость доказана. Начнём с того, что диск АВ и диск Земля связаны жестко, следовательно, образуют один общий диск. Обозначим его Д1 и обведём пунктиром.
|
|
Далее рассмотрим соединения трёх дисков: Д1, CD и DE. Диски CD и DE соединены шарниром (D), диски Д1 и CD двумя стержнями (BC и G), и наконец, диски DE и Земля соединены двумя стержнями (H и K). В целом получается соединение трёх дисков при помощи шарнира и четырёх стержней. Такой стандартный способ соединения трёх дисков есть. Однако необходимо доказать, что система не является мгновенно изменяемой. Для этого определим положение фиктивных шарниров, которые находятся на пересечении стержней. Это шарнир Ш1 (на пересечении стержней BC и G) и шарнир, положение которого уходит в бесконечность, т.к. стержни H и K параллельны. Шарниры не лежат на одной прямой. Таки образом мы доказали, что диски Д1, CD и DE образуют общий диск. Обозначим его Д2 и обведём точечной линией.
Диск Д2 связан c диском EF шарниром E и стержнем L (стержень не пересекает шарнир). Таким образом, они образуют общий диск.
Окончательный вывод: система в целом является диском, следовательно, она ГН и СО.
Контрольные вопросы к разделу 1
1. Какие системы называются геометрически неизменяемыми?
2. Каков порядок кинематического анализа систем? Количественная и качественные оценки неизменяемости системы.
3. Покажите на примерах простейшие способы образования геометрически неизменяемых систем.
|
|
4. Какие системы называются мгновенно изменяемыми?
5. Приведите пример системы близкой к мгновенно изменяемой.
6. Назовите основные типы опорных устройств, их статические и кинематические характеристики.
7. Почему сооружение называется статически определимым?
Пример теста на защиту темы:
 1. Число степеней свободы рамы равно (1) 1. Число степеней свободы рамы равно (1)
|
|
 в рамах, чтобы они стали статически в рамах, чтобы они стали статически
              определимыми? (2) определимыми? (2)
|
|
|
|
 7. Число степеней свободы фермы равно (1) 7. Число степеней свободы фермы равно (1)
|
8. Сколько шарниров нужно добавить, чтобы
 балка стала статически определимой? (1) балка стала статически определимой? (1)
|






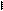




 Сколько связей нужно удалить
Сколько связей нужно удалить  Удаление какой пронумерованной связи
Удаление какой пронумерованной связи 
 Какое минимальное число опорных
Какое минимальное число опорных  Удаление какой пронумерованной связи
Удаление какой пронумерованной связи