Раздел 8. Обыкновенные дифференциальные уравнения Самостоятельная работа №1
1.Найти общее решение уравнений.
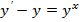
| 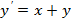
| ||
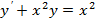
| 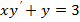
| ||
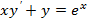
| 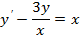
|
2. Найти частные решения уравнений, удовлетворяющие начальным условиям:
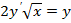
| 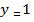 при при 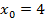
| |
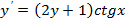
| 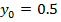 при при 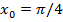
| |
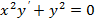
| 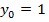 при при 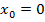
|
3.Проинтегрируйте дифференциальные уравнения с разделяющимися переменными. Если даны начальные условия, найдите частные решения:
1. 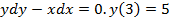 ; 2.
; 2.  ; 3.
; 3. 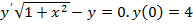
4.Проинтегрируйте однородные дифференциальные уравнения:
1. 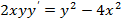 ; 2.
; 2. 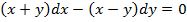 ; 3.
; 3. 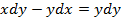
5.Проинтегрируйте линейные дифференциальные уравнения и уравнения Бернулли:
1. 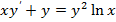
2. 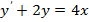
3. 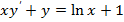
6.Решить уравнения Бернулли.
1. 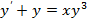
2. 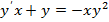
3. 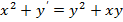
7. Определите тип дифференциального уравнения:
1. 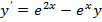
2. 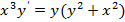
3. 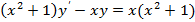
8.Решить уравнение:
1. 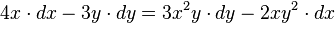
2. 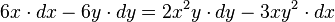
3. 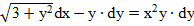
Самостоятельная работа №2
1.Найдите частное решение данного уравнения
а) 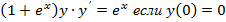
б) 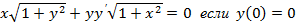
2. Решить уравнение:
а) 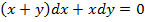
б) 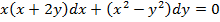
3. Решить уравнение:
1) 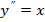
2) 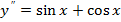
3) 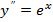
4. Найдите частное решение уравнения 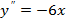 удовлетворяющее начальным условиям
удовлетворяющее начальным условиям 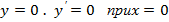
5. Решить уравнение:
1) 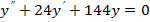
2) 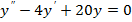
6.Найти частное решение дифференциального уравнения
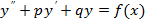 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 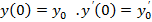 .
.
1. 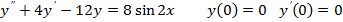
2. 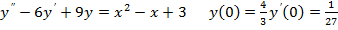
3. 
7. Найти общее решение дифференциального уравнения.
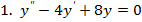
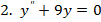
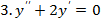
Самостоятельная работа №3
1. Решить однородное дифференциальное уравнение третьего порядка
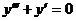
2. Решить однородное дифференциальное уравнение четвертого порядка
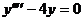
3. Решить однородное дифференциальное уравнение шестого порядка
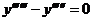
4. Найти общее решение дифференциального уравнения третьего порядка
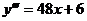 и выделить из полученного общего решения частное решение, удовлетворяющее начальным условиям:
и выделить из полученного общего решения частное решение, удовлетворяющее начальным условиям:
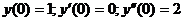 .
.
5. Решить уравнение:
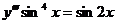
6. Решить уравнение:
7. 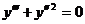
8. Решить уравнение
9. 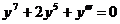
10. Решить уравнение
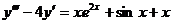
11. Найдите общее решение линейного однородного дифференциального уравнения третьего порядка с постоянными коэффициентами 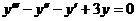 .
.
12. Найдите общее решение дифференциального уравнения 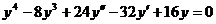 .
.
13. Проинтегрируйте линейное однородное дифференциальное уравнение четвертого порядка с постоянными коэффициентами 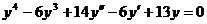 .
.
14. Найдите общее решение ЛОДУ с постоянными коэффициентами 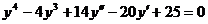
15. Найдите общее решение дифференциального уравнения 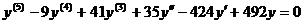
16. Найти общее решение ЛОДУ 3-го порядка с постоянными коэффициентами:
17. 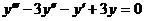 .
.
18. Найти общее решение ДУ
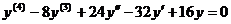
19. Проинтегрировать ЛОДУ 4-го порядка с постоянными коэффициентами 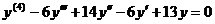 .
.
Самостоятельная работа №4
1. Дана система линейных дифференциальных уравнений с постоянными коэффициентами.
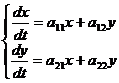
Требуется: 1) найти общее решение системы с помощью характеристического уравнения; 2) записать в матричной форме данную систему и её решение.
1. 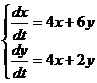 2.
2. 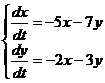
3. 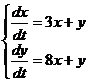 4.
4. 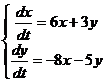
2.Проинтегрировать систему ДУ.
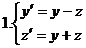
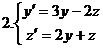
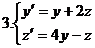
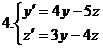
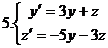
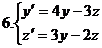
Вопросы для самопроверки
1. Какое уравнение называется дифференциальным?
2. Что такое порядок дифференциального уравнения?
3. Что называется решением дифференциального уравнения? Какое из решений называется общим, а какое частным?
4. Сформулируйте понятие задачи Коши.
5. Какое уравнение называется дифференциальным уравнением первого порядка с разделяющимися переменными? Как оно интегрируется?
6. Приведите формулы общих решений линейных однородных дифференциальных уравнений второго порядка.
7. Как ставится задача Коши для дифференциального уравнения первого порядка?
8. Что называется дифференциальным уравнением первого порядка с разделяющимися переменными?
9. В чем состоит схема решения дифференциального уравнения первого порядка с разделяющимися переменными?
10. Что называется однородным дифференциальным уравнением первого порядка?
11. В чем состоит схема решения однородного дифференциального уравнения первого порядка?
12. Что называется линейным неоднородным дифференциальным уравнением первого порядка?
13. В чем состоит схема решения линейного неоднородного дифференциального уравнения первого порядка?
14. Что называется уравнением Бернулли?
15. В чем состоит схема решения уравнения Бернулли?
16. Какие дифференциальные уравнения второго порядка решаются при помощи понижения порядка?
17. В чем состоит схема решения дифференциальных уравнений, допускающих понижение порядка?
Домашняя контрольная работа №1
1.Найти частные решения уравнений, удовлетворяющие начальным условиям:
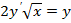 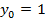
| при 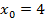
|
2.Найти общее решение: 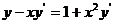
3. Найти общее решение уравнений 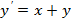
4.Решить уравнения Бернулли
1. 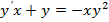
2. 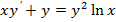
3. 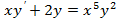
4. 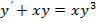
5. Проинтегрируйте дифференциальные уравнения с разделяющимися переменными. Если даны начальные условия, найдите частные решения:
1. 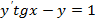 ,
, 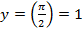
2. 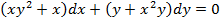
3. 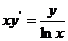 ,
, 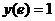
6. Проинтегрируйте однородные дифференциальные уравнения:
1. 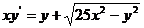
2. 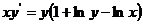
3. 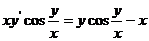
7. Решить уравнение:
1. 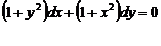
2.