1. Из колоды в 32 карты наудачу выбираются две карты (прикуп при игре в преферанс). Событие А = (обе карты - тузы).
2. При наборе телефонного номера абонент забыл две последние цифры и набирает их наудачу, помня только, что они нечетные и разные. Событие А = (номер набран верно).
3. Из шестизначных телефонных номеров, не содержащих одинаковых цифр, наудачу выбирается один. Событие А = (цифры номера следуют в порядке возрастания).
4. Три игральные кости подбрасываются один раз. События: А = (сумма очков, выпавших на верхних гранях костей, равна 12); В= (на первой кости выпало четное число очков); С = (на всех костях выпало одинаковое число очков).
5. Три занумерованных шара раскладываются наудачу по трем ящикам. В каждый ящик может поместиться любое число шаров. События: А = (все шары попадут в один ящик); В = (в первый ящик попадут два шара); С = (в каждый ящик попадет по одному шару).
6. В каждый разряд восьмиразрядного двоичного числа случайным образом записывается либо 0, либо 1. События: A={количество записанных нулей равно количеству единиц}; В = {в самый старший и самый младший разряды записаны нули}.
7. В розыгрыше первенства по баскетболу участвуют 18 команд, занумерованных от 1 до 18. Из них по жребию формируются две подгруппы по 9 команд в каждой. События А,В,С состоят в том, что команды с номерами 1 и 18 попадут соответственно: а) в первую подгруппу; Ь) в одну подгруппу; с) в разные подгруппы.
8. Из урны, содержащей 10 шаров, занумерованных от 1 до 10, наудачу один за другим извлекают все находящиеся в ней шары. События: А = {последним извлечен шар с номером 5}; В = {первым извлечен шар с нечетным номером}; С = ^при извлечении четные и нечетные номера шаров чередовались}.
|
|
9. N различных предметов случайным образом распределяются между т лицами (m<N), причем каждый может получить любое число предметов из имеющихся. События: А = {каждому достанется хотя бы по одному предмету}; В = {хотя бы одному лицу ничего не достанется}; С = {все предметы достанутся одному лицу}; D = {ровно двум лицам ничего не достанется}.
10. При игре в бридж колода в 52 карты случайным образом распределяется между четырьмя игроками (по 13 карт каждому). События: А = {каждому достались карты только одной масти}; В = {первому игроку достались все фигуры (валеты, дамы, короли)}; С = {каждому достался туз}.
Самостоятельная работа №3
1.Дискретная случайная величина X задана законом распределения
| X | -4 | ||
| p | 0.2 | p(X=6) | 0.15 |
Неизвестная вероятность p(X=6) равна
1) 0.35;
2) 0.65;
3) 1,0.
2. Дискретная случайная величина X задана законом распределения
| X | ||||
| p | 0.3 | 0.1 | 0.2 | 0.4 |
Вероятность события 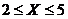 равна
равна
1) 0.6;
2) 0.3;
3) 0,1.
3. Дискретная случайная величина X задана законом распределения
| X | ||||
| p | 0.3 | 0.1 | 0.2 | 0.4 |
Вероятность события 
1) 0;
2) 0.3;
3) 0.7.
4. Дискретная случайная величина X задана законом распределения
| X | -1 | |||
| p | 0.4 | 0.3 | 0.1 | 0.2 |
Вероятность события 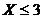 равна
равна
1) 0.8;
2) 0.7;
3) 0.1.
5. Дискретная случайная величина X задана законом распределения
| X | ||||
| p | 0.3 | 0.1 | 0.2 | 0.4 |
Вероятность события 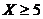 равна
равна
1) 0.4;
2) 0.6;
3) 1.0.